人教版数学二年级上册 简单的组合问题 课件(17张ppt)
文档属性
| 名称 | 人教版数学二年级上册 简单的组合问题 课件(17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-04 18:24:25 | ||
图片预览



文档简介
(共17张PPT)
数学广角——搭配(一)
8
简单的组合问题
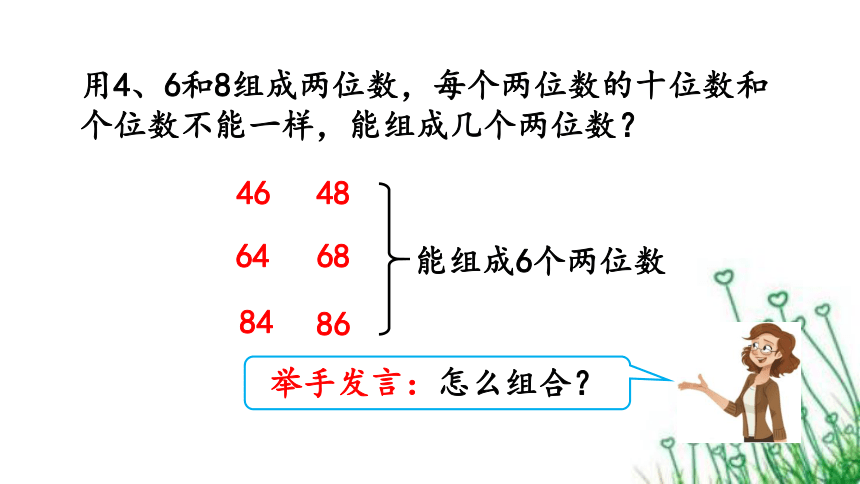
用4、6和8组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
46
64
48
84
68
86
能组成6个两位数
举手发言:怎么组合?
有3个数, 5、 7、 9,任意选取其中2个求和,得数有几种可能?
把这3个数两个两个地组合在一起求和,根据和的大小确定得数有几种可能。
小组讨论:该怎样解决这个问题?
加数 加数 和
12
14
12
16
14
16
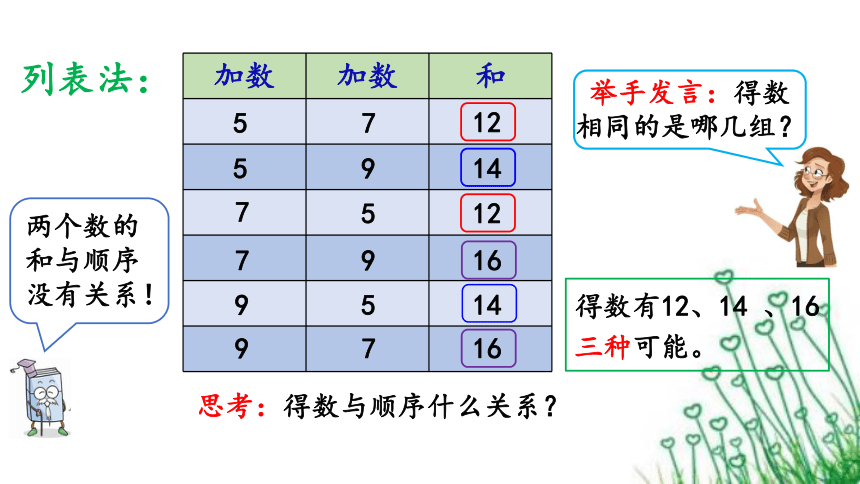
得数有12、14 、16三种可能。
5
5
7
7
9
9
7
9
5
9
5
7
两个数的和与顺序没有关系!
列表法:
举手发言:得数相同的是哪几组?
思考:得数与顺序什么关系?
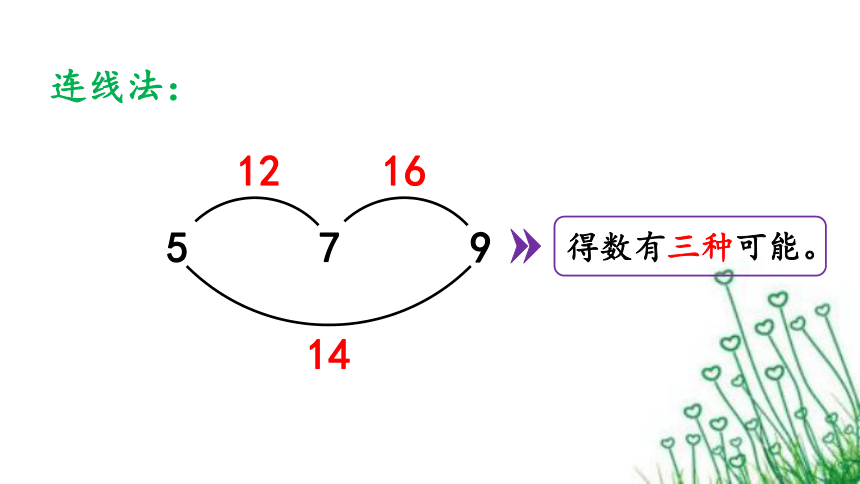
5 7 9
12
16
14
得数有三种可能。
连线法:
用两个数字组数,只要把这两个数字调换位置,组成的两个数就不同。
两个数的和,无论两个数怎样调换位置,和都不变。
排列与事物的顺序有关,组合与事物的顺序无关。
举手发言:组合与排列的区别是什么?
组合与排列不同,它与顺序无关,可利用列表法或连线法来解决组合的问题。
归纳总结:
每两个人握一次手,三个人一共握几次手?
答:三个人一共握3次手。
买一个拼音本,可以怎样付钱?
5角
拼音本
×5
×3
一共有4种付钱的方式。
每两个小朋友握1次手,4个小朋友一共要握几次手?写一写。(写序号)
①
②
③
④
①②,①③,①④,②③,②④,③④。
一共要握6次手。
兰兰有3顶不同的帽子和3条不同的围巾,她有( )种不同的搭配方法。
9
下面有四种球,每班可以借其中的两种,有多少种不同的搭配方法?
① ② ③ ④
①②
①③
①④
②③
②④
③④
有6种不同的搭配方法。
选一选。
(1)明明、聪聪和刚刚三人参加乒乓球比赛,每两人之间比赛一场,一共要比赛( )场。
A.3 B.4 C.6 D.8
(2)2件上衣和2条裤子,一共有( )种不同的穿法。
A.1 B.2 C.3 D.4
A
D
一种饮品只能搭配一种食品,有几种不同的搭配方法?
有6种不同的搭配方法。
下面有3本书,明明想买其中的两本,有多少种买法?
答:有3种买法。
故事汇
大科学
奥数
这节课你们都学会了哪些知识?
解决组合问题
1.要按照一定的规律去思考
(1)列表法
(2)连线法
2.与排列不同,组合与顺序没有关系。
简单的组合问题
加数 加数 和
12
14
5
5
7
9
5 7 9
12
16
14
谢谢!
数学广角——搭配(一)
8
简单的组合问题
用4、6和8组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
46
64
48
84
68
86
能组成6个两位数
举手发言:怎么组合?
有3个数, 5、 7、 9,任意选取其中2个求和,得数有几种可能?
把这3个数两个两个地组合在一起求和,根据和的大小确定得数有几种可能。
小组讨论:该怎样解决这个问题?
加数 加数 和
12
14
12
16
14
16
得数有12、14 、16三种可能。
5
5
7
7
9
9
7
9
5
9
5
7
两个数的和与顺序没有关系!
列表法:
举手发言:得数相同的是哪几组?
思考:得数与顺序什么关系?
5 7 9
12
16
14
得数有三种可能。
连线法:
用两个数字组数,只要把这两个数字调换位置,组成的两个数就不同。
两个数的和,无论两个数怎样调换位置,和都不变。
排列与事物的顺序有关,组合与事物的顺序无关。
举手发言:组合与排列的区别是什么?
组合与排列不同,它与顺序无关,可利用列表法或连线法来解决组合的问题。
归纳总结:
每两个人握一次手,三个人一共握几次手?
答:三个人一共握3次手。
买一个拼音本,可以怎样付钱?
5角
拼音本
×5
×3
一共有4种付钱的方式。
每两个小朋友握1次手,4个小朋友一共要握几次手?写一写。(写序号)
①
②
③
④
①②,①③,①④,②③,②④,③④。
一共要握6次手。
兰兰有3顶不同的帽子和3条不同的围巾,她有( )种不同的搭配方法。
9
下面有四种球,每班可以借其中的两种,有多少种不同的搭配方法?
① ② ③ ④
①②
①③
①④
②③
②④
③④
有6种不同的搭配方法。
选一选。
(1)明明、聪聪和刚刚三人参加乒乓球比赛,每两人之间比赛一场,一共要比赛( )场。
A.3 B.4 C.6 D.8
(2)2件上衣和2条裤子,一共有( )种不同的穿法。
A.1 B.2 C.3 D.4
A
D
一种饮品只能搭配一种食品,有几种不同的搭配方法?
有6种不同的搭配方法。
下面有3本书,明明想买其中的两本,有多少种买法?
答:有3种买法。
故事汇
大科学
奥数
这节课你们都学会了哪些知识?
解决组合问题
1.要按照一定的规律去思考
(1)列表法
(2)连线法
2.与排列不同,组合与顺序没有关系。
简单的组合问题
加数 加数 和
12
14
5
5
7
9
5 7 9
12
16
14
谢谢!
