探索规律（一）

(共24张PPT)
湖北省秭归县教育科研信息中心
何 训 光
北师大版数学教材七年级上册
第三章 字母表示数
湖北省秭归县教育科研信息中心 何 训 光
湖北省宜昌市第九中学 杨 立 权
1
2
3
4
5
6
7
8
9
10
11
……
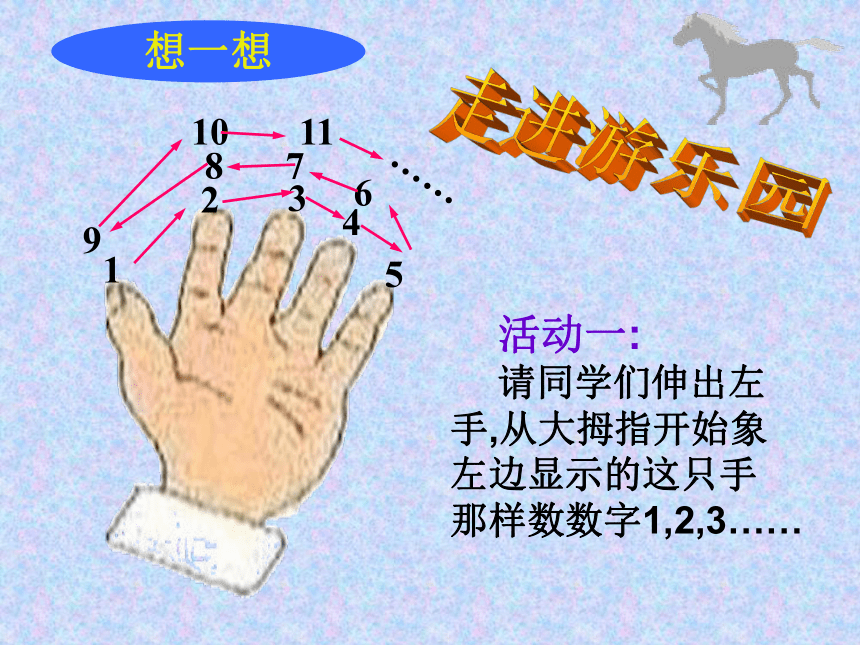
活动一:
请同学们伸出左
手,从大拇指开始象
左边显示的这只手
那样数数字1,2,3……
想一想
1、数到20时，刚好落在哪个手指上？
2、数到200时又会落在哪个手指上呢？2000呢
想一想？
观察下表，按数数的方法填写下表
大拇指 食指 中指 无名指 小指
1 2 3 4 5
一展身手
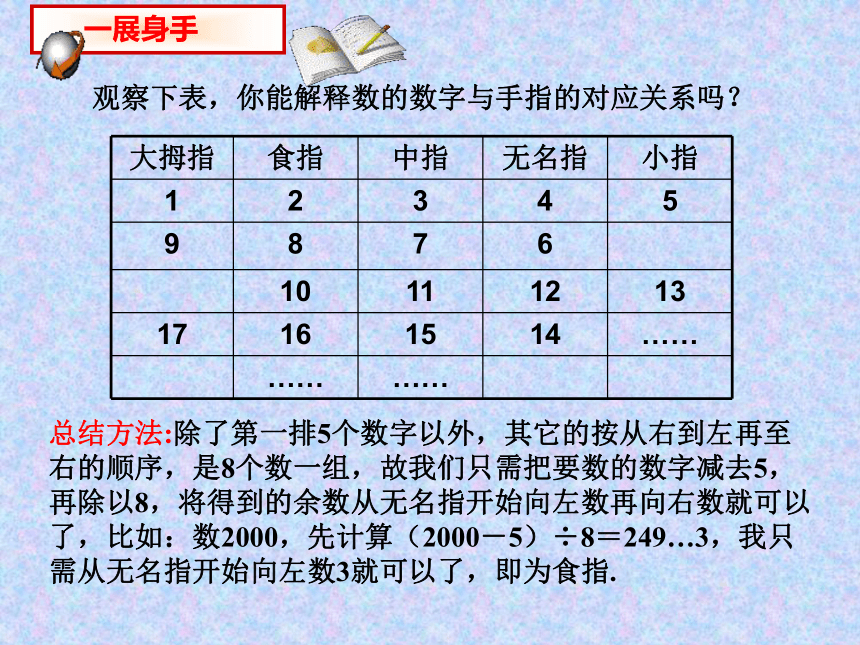
观察下表，你能解释数的数字与手指的对应关系吗？
大拇指 食指 中指 无名指 小指
1 2 3 4 5
9 8 7 6
10 11 12 13
17 16 15 14 ……
…… ……
总结方法:除了第一排5个数字以外，其它的按从右到左再至右的顺序，是8个数一组，故我们只需把要数的数字减去5，再除以8，将得到的余数从无名指开始向左数再向右数就可以了，比如：数2000，先计算（2000－5）÷8＝249…3，我只需从无名指开始向左数3就可以了，即为食指.
一展身手
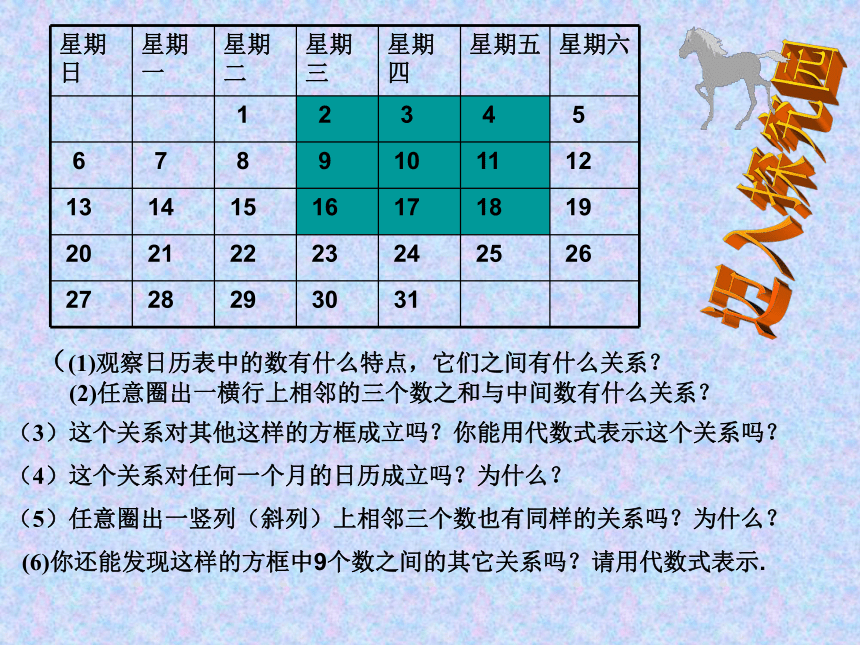
（(1)观察日历表中的数有什么特点，它们之间有什么关系？
(2)任意圈出一横行上相邻的三个数之和与中间数有什么关系？
（3）这个关系对其他这样的方框成立吗？你能用代数式表示这个关系吗？
（4）这个关系对任何一个月的日历成立吗？为什么？
（5）任意圈出一竖列（斜列）上相邻三个数也有同样的关系吗？为什么？
(6)你还能发现这样的方框中9个数之间的其它关系吗？请用代数式表示.
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
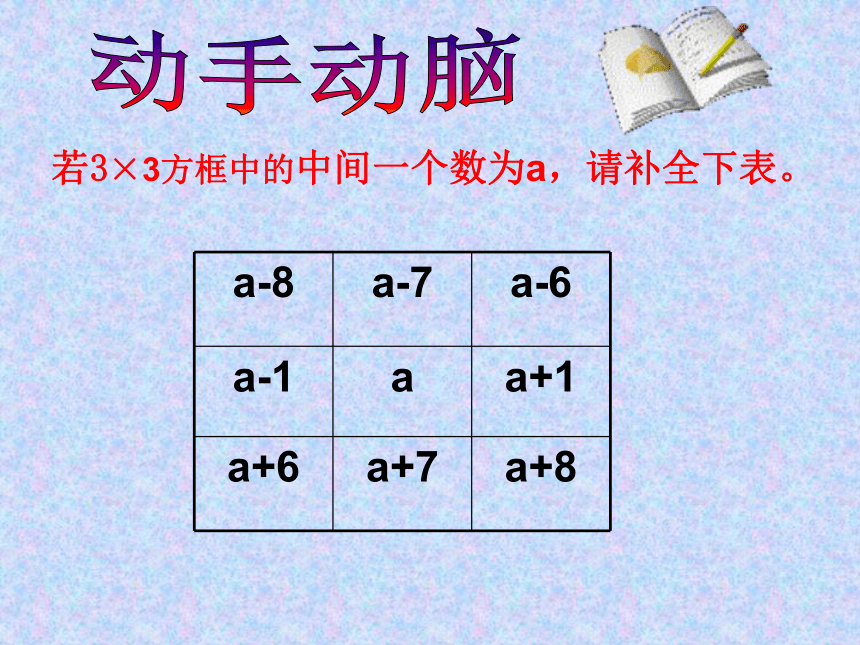
若3×3方框中的中间一个数为a，请补全下表。
a
若3×3方框中的中间一个数为a，请补全下表。
a-8 a-7 a-6
a-1 a a+1
a+6 a+7 a+8
拖动下列方框,你会发现什么
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
活动二:
在日历中,从其它区域上考察还能发现哪些规律
如: 十字形区域,H形区域 , W形区域 , X形区域等.
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
星期日 星期一 星期二 星期三 星期四 星期五 星期六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
在一个10×10的方框中框出9个数，如上表,请有兴趣的同学在课后作进一步的探讨，我相信大家一定会有更多的发现和收获。我更相信未来的数学家就在我们身边。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
课后思考
活动三：让学生拿出一张长方形的纸对折，可以得到一条折痕，继续对折，对折时每次折痕与上次的折痕保持平行，连续折6次后，可以得到几条折痕？如果对折10次呢？对折n次呢？
对折1次,折痕为1.
对折2次，折痕为3，即3=22-1
对折3次，折痕为7，即7=23-1
对折4次，折痕为15,即15=24-1
……
对折5次，折痕为31,即31=25-1。
对折n次，折痕为2n-1。
大家来归纳
1、完成表格内容:
类 别 四棱柱 五棱住 十棱住 … n棱住
顶点数
棱 数
面 数
（1）填写下表
……
三角形个数 1 2 3 4 5
火柴棒根数
（2）照这样的规律搭下去，搭n个这样的三角形需要多少根火柴棒？
2、用火柴棒按下图方式搭三角形：
,
3、瑞士中学教师巴尔末成功地从光谱数据
A、
B、
C、
D、
,
,
……中得到巴尔末公式,从而打开了光谱奥
妙的大门,按照这种规律写出的第七个数据( ).
知识点延伸
2、探索规律的一般方法：
1、探索规律的主要过程：
特殊——一般——特殊
(1)寻找数量关系；
(2)用代数式表示规律；
(3)验证规律。
1．研究下列算式，你发现了什么规律？用字母表示这个规律。
　1×5+4=9=3×3；
2×6+4=16=4×4；
3×7+4=25=5×5；
4×8+4=36=6×6；
………………
用n表示自然数,规律是： 。
想一想
2．图①是一个三角形，分别连接这个三角形三边的中点得到图②，再分别连接图②中间的小三角形三边的中点，得到图③。图①图②图③
(1)图②有 个三角形；图③有 个三角形。
(2)按上面的方法继续下去，第10个图有 个三角形，第n个图形中有 个三角形（用含n的代数式表示）。
图1
图2
图3
在一个10×10的方框中框出9个数，如下表,请有兴趣的同学在课后作进一步的探讨，我相信大家一定会有更多的发现和收获。我更相信未来的数学家就在我们身边。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
课 后
作 业