解直角三角形--仰角俯角
文档属性
| 名称 | 解直角三角形--仰角俯角 |  | |
| 格式 | rar | ||
| 文件大小 | 390.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-04 23:16:00 | ||
图片预览



文档简介
(共24张PPT)
听老师讲仰角俯角及大海里航行的船哦!
快走啊 刚结束了第三次月考不要松劲啊!
中山市三乡南峰中学 姜绍泽
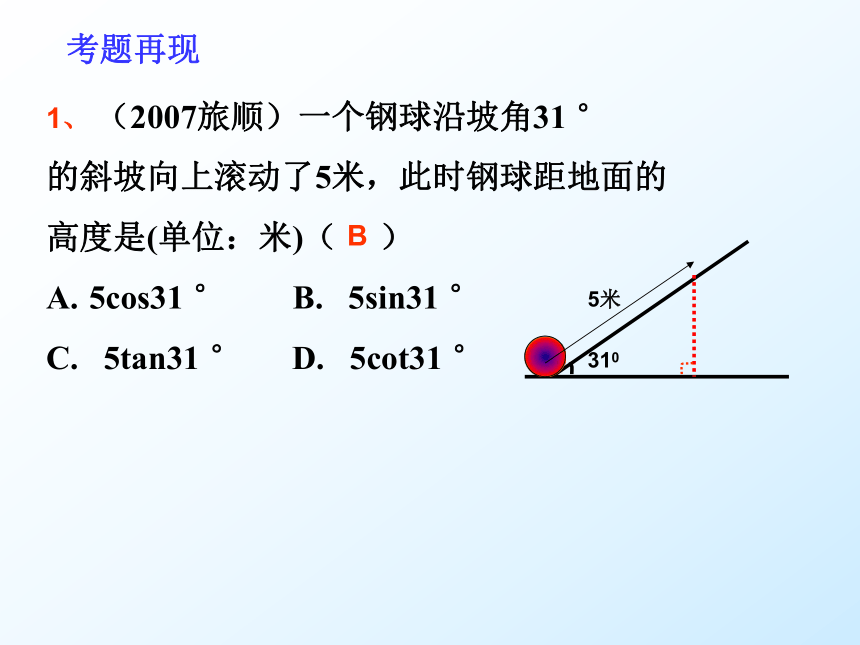
1、 (2007旅顺)一个钢球沿坡角31 °
的斜坡向上滚动了5米,此时钢球距地面的
高度是(单位:米)( )
5cos31 ° B. 5sin31 °
C. 5tan31 ° D. 5cot31 °
考题再现
B
310
5米
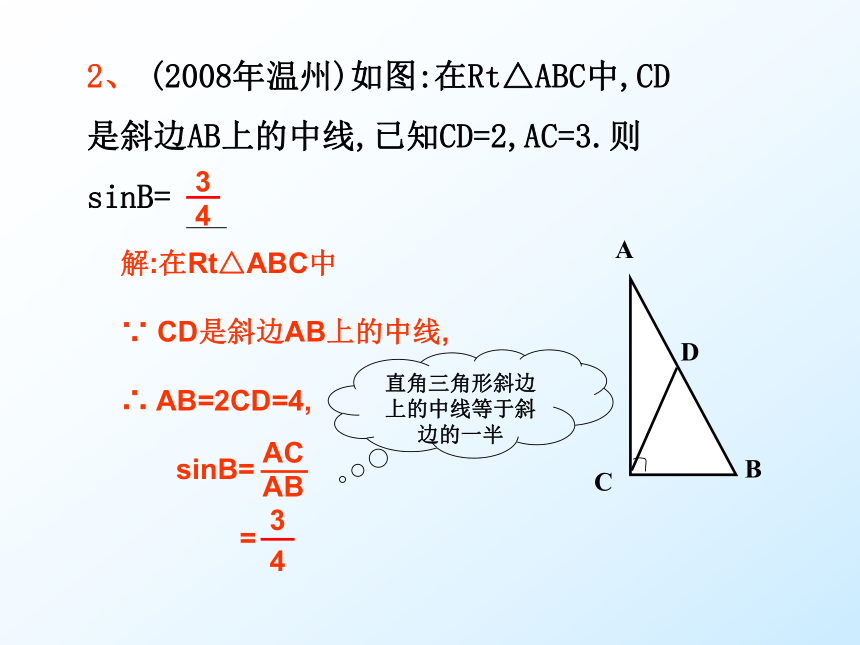
2、 (2008年温州)如图:在Rt△ABC中,CD
是斜边AB上的中线,已知CD=2,AC=3.则
sinB=
解:在Rt△ABC中
∵ CD是斜边AB上的中线,
∴ AB=2CD=4,
sinB=
=
AC
AB
3
4
A
B
C
D
3
4
直角三角形斜边上的中线等于斜边的一半
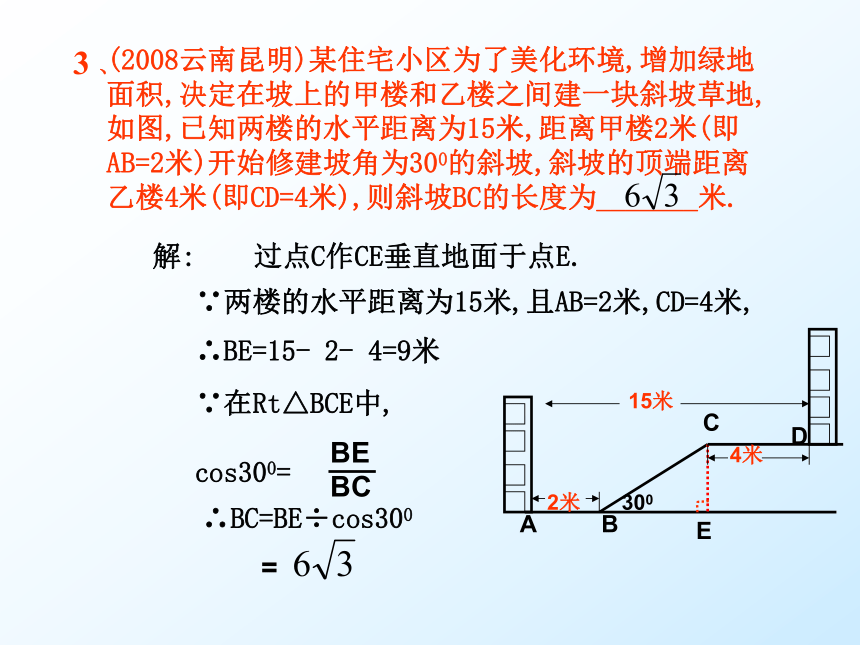
3 、
(2008云南昆明)某住宅小区为了美化环境,增加绿地面积,决定在坡上的甲楼和乙楼之间建一块斜坡草地,如图,已知两楼的水平距离为15米,距离甲楼2米(即AB=2米)开始修建坡角为300的斜坡,斜坡的顶端距离乙楼4米(即CD=4米),则斜坡BC的长度为_______米.
300
C
D
A
B
E
解: 过点C作CE垂直地面于点E.
∵两楼的水平距离为15米,且AB=2米,CD=4米,
∴BE=15- 2- 4=9米
∵在Rt△BCE中,
cos300=
∴BC=BE÷cos300
BE
BC
=
15米
2米
4米
(2007南充)如图:一艘轮船由海平面上A地出发向南偏西400的方向行驶40海里到达B地,再由B地向北偏西200的方向行驶40海里到达C地,则A,C两地的距离为 ____
北
A
北
B
C
400
40海里
D
200
有一个角是600的三角形是等边三角形
答:货轮无触礁危险。
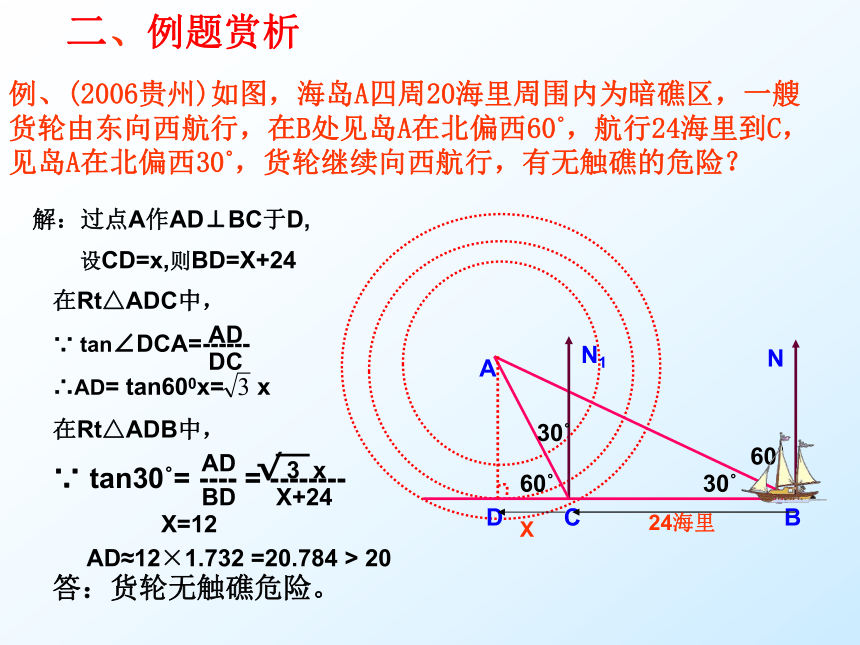
在Rt△ADC中,
∵ tan∠DCA=------
∴AD= tan600x= x
在Rt△ADB中,
∵ tan30 = ---- = --------
AD≈12×1.732 =20.784 > 20
解:过点A作AD⊥BC于D,
A
B
D
C
N
N1
30
60
二、例题赏析
24海里
X
AD
DC
AD
BD
3 x
√
X=12
X+24
设CD=x,则BD=X+24
例、(2006贵州)如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60 ,航行24海里到C,见岛A在北偏西30 ,货轮继续向西航行,有无触礁的危险?
30
60
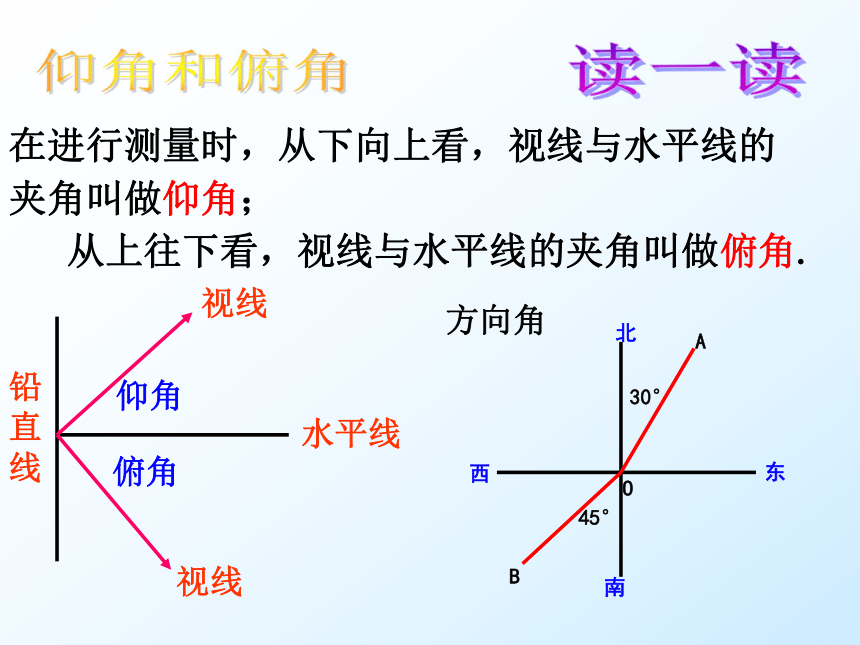
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的 夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
30°
45°
B
O
A
东
西
北
南
方向角
例2:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高
α=30°
β=60°
120
A
B
C
D
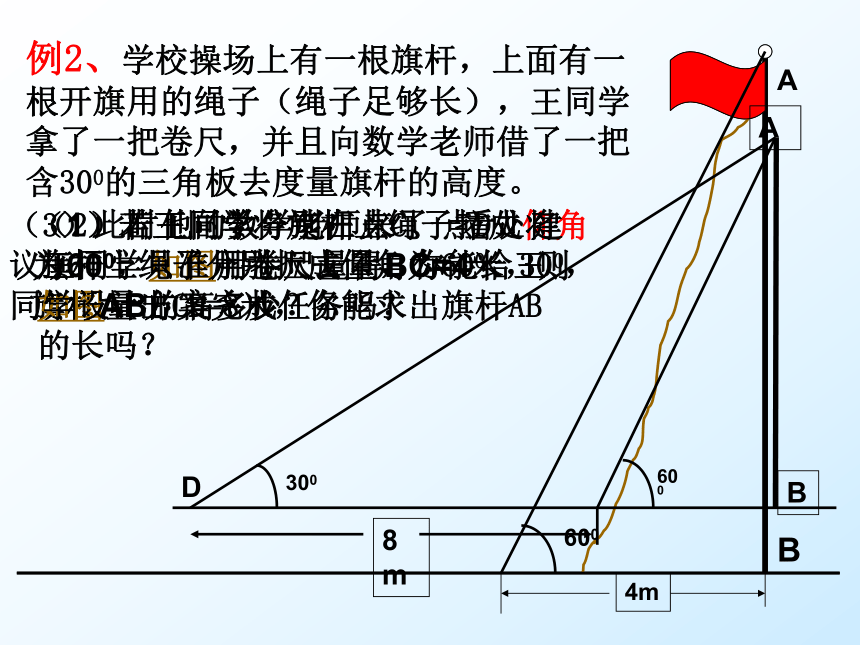
例2、学校操场上有一根旗杆,上面有一根开旗用的绳子(绳子足够长),王同学拿了一把卷尺,并且向数学老师借了一把含300的三角板去度量旗杆的高度。
(1)若王同学将旗杆上绳子拉成仰角为600,如图用卷尺量得BC=4米,则旗杆AB的高多少?
(2)若王同学分别在点C、点D处将旗杆上绳子分别拉成仰角为600、300,如图量出CD=8米,你能求出旗杆AB的长吗?
(3)此时他的数学老师来了一看,建议王同学只准用卷尺去量,你能给王同学设计方案完成任务吗?
A
B
4m
600
A
B
D
8m
300
600
1、如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)
1.20
22.7
=220
2、在山脚C处测得山顶A的仰角为45°。问题如下:(1)沿着水平地面向前300米到达D点,在D点测得山顶A的仰角为600 , 求山高AB。
D
A
B
C
45°
60°
x
A
B
C
2、在山脚C处测得山顶A的仰角为450。问题如下:
变式: 沿着坡角为30 °的斜坡前进300米到达D点,在D点测得山顶A的仰角为600 ,求山高AB。
30°
D
E
F
x
x
3、在山顶上处D有一铁塔,在塔顶B处测得地面上一点A的俯角α=60o,在塔底D测得点A的俯角β=45o,已知塔高BD=30米,求山高CD。
A
B
C
α
D
β
1.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=16031`,求飞机A到控制点B的距离.(精确到1米)
α
A
B
C
2. 两座建筑AB及CD,其地面距离AC为50.4米,从AB的顶点B测得CD的顶部D的仰角β=250,测得其底部C的俯角a=500, 求两座建筑物AB及CD的高.(精确到0.1米)
课本P92 例4
3.国外船只,除特许外,不得进入我国海洋100海里以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条直线,一外国船只在P点,在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时是否要向外国船只发出警告,令其退出我国海域.
P
A
B
建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为50°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)
B
A
C
D
40
(课本93页)
(2007淄博)王英同学从A地沿北偏西60 方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地多少距离?
A
B
C
北
南
西
东
D
E
600
100m
200m
(2007年昆明)如图,AB和CD是同一地面上的两座相距36米的楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为450,楼底D的俯角为300,求楼CD的高?(结果保留根号)
300
450
A
B
C
D
36
4、如图,为了测量高速公路的保护石堡坎与地面的倾斜角∠BDC是否符合建筑标准,用一根长为10m的铁管AB斜靠在石堡坎B处,在铁管AB上量得AF长为1.5m,F点离地面的距离为0.9m,又量出石堡坎顶部B到底部D的距离为 m ,这样能计算出∠BDC吗?若能,请计算出∠BDC的度数,若不能,请说明理由。
例4.海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
F
60°
12
30°
例3. 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远? (精确到0.01海里)
65°
34°
P
B
C
A
80
1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。
2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
听老师讲仰角俯角及大海里航行的船哦!
快走啊 刚结束了第三次月考不要松劲啊!
中山市三乡南峰中学 姜绍泽
1、 (2007旅顺)一个钢球沿坡角31 °
的斜坡向上滚动了5米,此时钢球距地面的
高度是(单位:米)( )
5cos31 ° B. 5sin31 °
C. 5tan31 ° D. 5cot31 °
考题再现
B
310
5米
2、 (2008年温州)如图:在Rt△ABC中,CD
是斜边AB上的中线,已知CD=2,AC=3.则
sinB=
解:在Rt△ABC中
∵ CD是斜边AB上的中线,
∴ AB=2CD=4,
sinB=
=
AC
AB
3
4
A
B
C
D
3
4
直角三角形斜边上的中线等于斜边的一半
3 、
(2008云南昆明)某住宅小区为了美化环境,增加绿地面积,决定在坡上的甲楼和乙楼之间建一块斜坡草地,如图,已知两楼的水平距离为15米,距离甲楼2米(即AB=2米)开始修建坡角为300的斜坡,斜坡的顶端距离乙楼4米(即CD=4米),则斜坡BC的长度为_______米.
300
C
D
A
B
E
解: 过点C作CE垂直地面于点E.
∵两楼的水平距离为15米,且AB=2米,CD=4米,
∴BE=15- 2- 4=9米
∵在Rt△BCE中,
cos300=
∴BC=BE÷cos300
BE
BC
=
15米
2米
4米
(2007南充)如图:一艘轮船由海平面上A地出发向南偏西400的方向行驶40海里到达B地,再由B地向北偏西200的方向行驶40海里到达C地,则A,C两地的距离为 ____
北
A
北
B
C
400
40海里
D
200
有一个角是600的三角形是等边三角形
答:货轮无触礁危险。
在Rt△ADC中,
∵ tan∠DCA=------
∴AD= tan600x= x
在Rt△ADB中,
∵ tan30 = ---- = --------
AD≈12×1.732 =20.784 > 20
解:过点A作AD⊥BC于D,
A
B
D
C
N
N1
30
60
二、例题赏析
24海里
X
AD
DC
AD
BD
3 x
√
X=12
X+24
设CD=x,则BD=X+24
例、(2006贵州)如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60 ,航行24海里到C,见岛A在北偏西30 ,货轮继续向西航行,有无触礁的危险?
30
60
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的 夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
30°
45°
B
O
A
东
西
北
南
方向角
例2:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高
α=30°
β=60°
120
A
B
C
D
例2、学校操场上有一根旗杆,上面有一根开旗用的绳子(绳子足够长),王同学拿了一把卷尺,并且向数学老师借了一把含300的三角板去度量旗杆的高度。
(1)若王同学将旗杆上绳子拉成仰角为600,如图用卷尺量得BC=4米,则旗杆AB的高多少?
(2)若王同学分别在点C、点D处将旗杆上绳子分别拉成仰角为600、300,如图量出CD=8米,你能求出旗杆AB的长吗?
(3)此时他的数学老师来了一看,建议王同学只准用卷尺去量,你能给王同学设计方案完成任务吗?
A
B
4m
600
A
B
D
8m
300
600
1、如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)
1.20
22.7
=220
2、在山脚C处测得山顶A的仰角为45°。问题如下:(1)沿着水平地面向前300米到达D点,在D点测得山顶A的仰角为600 , 求山高AB。
D
A
B
C
45°
60°
x
A
B
C
2、在山脚C处测得山顶A的仰角为450。问题如下:
变式: 沿着坡角为30 °的斜坡前进300米到达D点,在D点测得山顶A的仰角为600 ,求山高AB。
30°
D
E
F
x
x
3、在山顶上处D有一铁塔,在塔顶B处测得地面上一点A的俯角α=60o,在塔底D测得点A的俯角β=45o,已知塔高BD=30米,求山高CD。
A
B
C
α
D
β
1.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=16031`,求飞机A到控制点B的距离.(精确到1米)
α
A
B
C
2. 两座建筑AB及CD,其地面距离AC为50.4米,从AB的顶点B测得CD的顶部D的仰角β=250,测得其底部C的俯角a=500, 求两座建筑物AB及CD的高.(精确到0.1米)
课本P92 例4
3.国外船只,除特许外,不得进入我国海洋100海里以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条直线,一外国船只在P点,在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时是否要向外国船只发出警告,令其退出我国海域.
P
A
B
建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为50°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)
B
A
C
D
40
(课本93页)
(2007淄博)王英同学从A地沿北偏西60 方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地多少距离?
A
B
C
北
南
西
东
D
E
600
100m
200m
(2007年昆明)如图,AB和CD是同一地面上的两座相距36米的楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为450,楼底D的俯角为300,求楼CD的高?(结果保留根号)
300
450
A
B
C
D
36
4、如图,为了测量高速公路的保护石堡坎与地面的倾斜角∠BDC是否符合建筑标准,用一根长为10m的铁管AB斜靠在石堡坎B处,在铁管AB上量得AF长为1.5m,F点离地面的距离为0.9m,又量出石堡坎顶部B到底部D的距离为 m ,这样能计算出∠BDC吗?若能,请计算出∠BDC的度数,若不能,请说明理由。
例4.海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
B
A
D
F
60°
12
30°
例3. 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远? (精确到0.01海里)
65°
34°
P
B
C
A
80
1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。
2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
