矩形
图片预览


文档简介
(共21张PPT)
有一个角是直角的平行四边形
矩形的定义:有一个角是直角的平行四边形叫做矩形。
画出一个矩形
大胆说出
展现自我
矩形是特殊的平行四边形,猜想它有哪些性质?
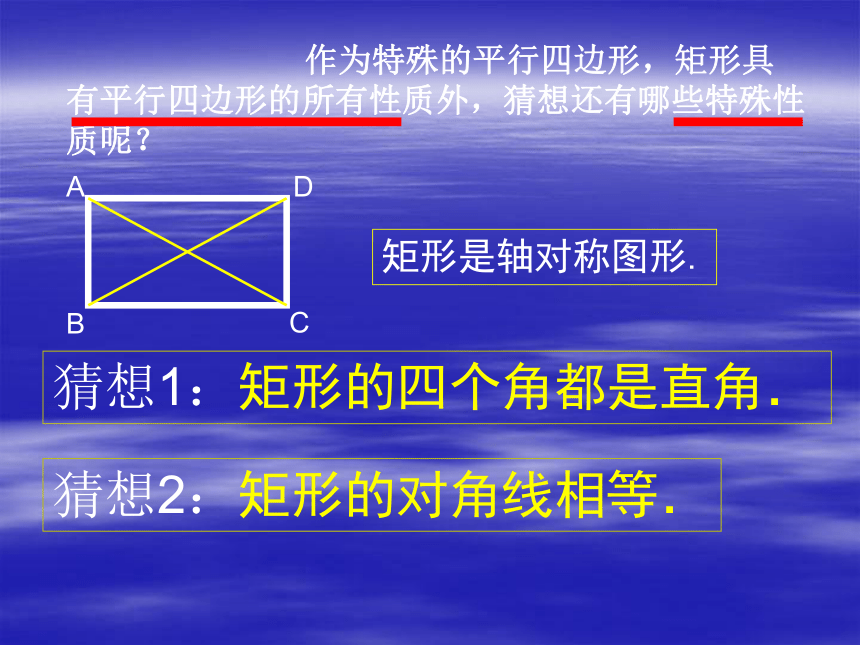
作为特殊的平行四边形,矩形具有平行四边形的所有性质外,猜想还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
矩形是轴对称图形.
A
B
C
D
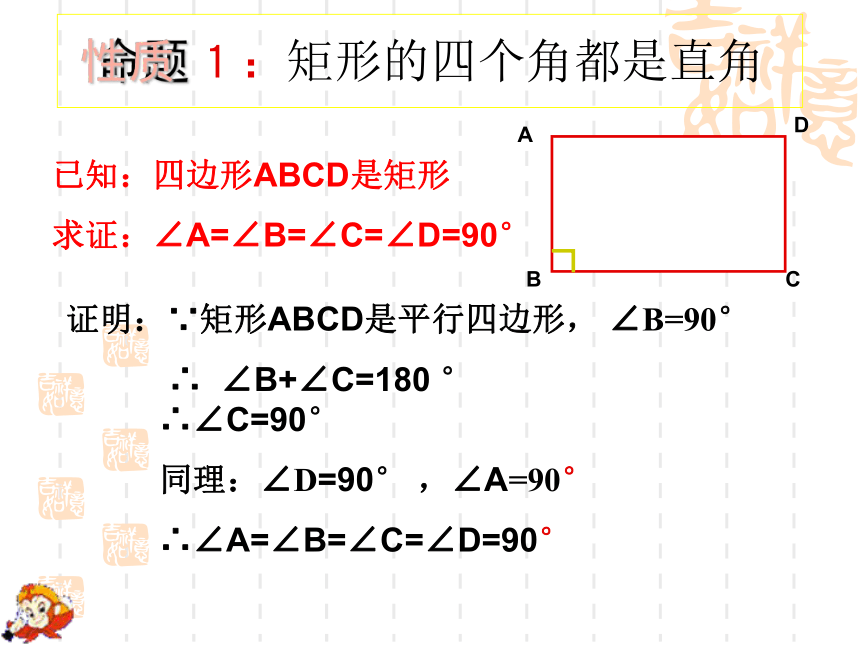
1:矩形的四个角都是直角
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
证明:∵矩形ABCD是平行四边形, ∠B=90°
∴ ∠B+∠C=180 °
∴∠C=90°
同理:∠D=90° ,∠A=90°
∴∠A=∠B=∠C=∠D=90°
命题
性质
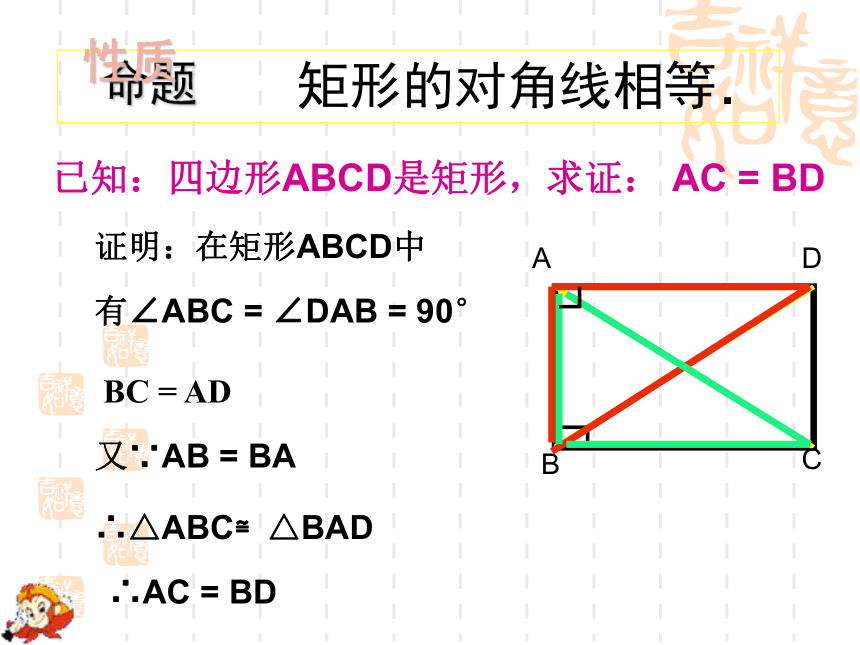
已知:四边形ABCD是矩形,求证: AC = BD
A
B
C
D
证明:在矩形ABCD中
有∠ABC = ∠DAB = 90°
BC = AD
又∵AB = BA
∴△ABC≌△BAD
∴AC = BD
2:矩形的对角线相等.
命题
性质
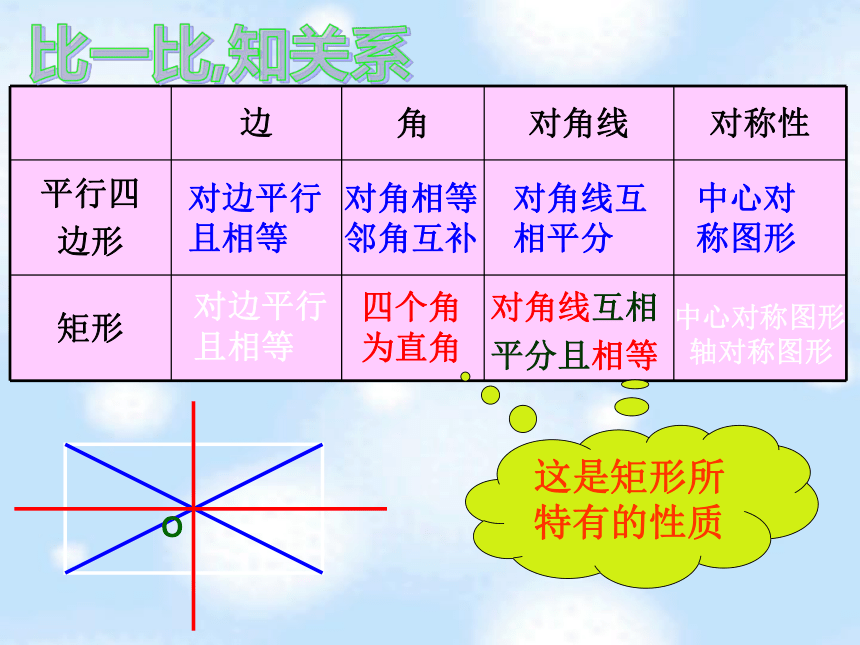
边 角 对角线 对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
O
这是矩形所特有的性质
边
对角线
角
A
B
C
D
O
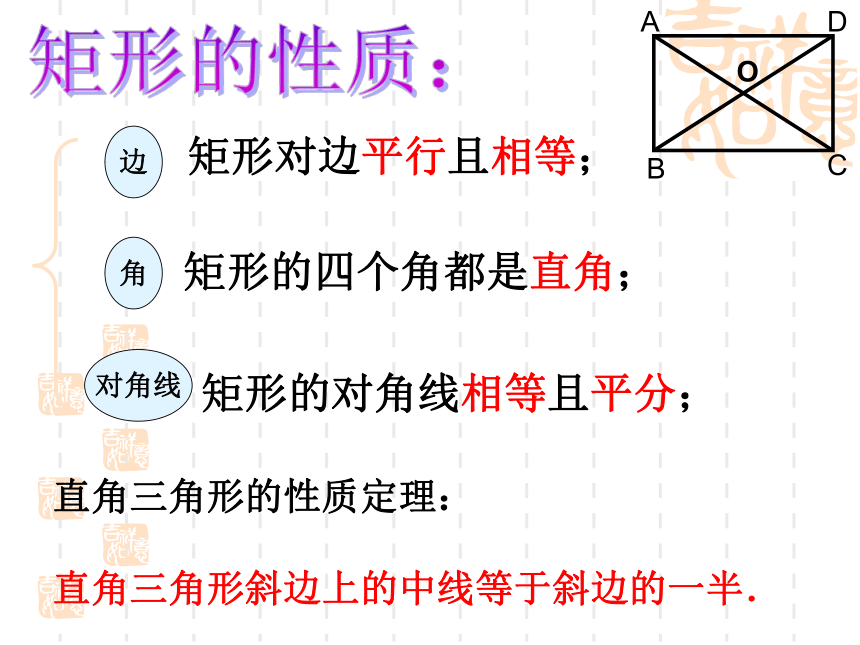
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且平分;
直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半.
O
D
C
B
A
┛
在Rt△ABD中,AO是斜边BD的中线
直角三角形的性质 :
直角三角形斜边上的中线等于斜边的一半。
则有:AO= BD
问题:矩形ABCD中,对角线AC、BD相交于点O.(1)图中有哪些相等的线段 (2)图中有哪些特殊形状的三角形
试试:用文字叙述
直角三角形的性质
在矩形ABCD中
AO=CO=BO=DO= AC= BD
例: 如图,矩形ABCD的两条对角线相交于点O, AB=4㎝,求矩形对角线的长?
解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)
D
C
B
A
O
已知对角线长是8cm,两对角线的一个夹角∠AOD是120°, 求矩形的宽AB与长BC的长.
变式:
小结:如果矩形两对角
线的夹角是60°或120°,
则其中必有等边三角形.
60°
4
∠AOB=60°,
AD = cm ,
1.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直
A
D
练一练
练一练
D
C
B
A
┓
3. 已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.
(1)若BD=3㎝,则AC=______ ㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.
6
5
10
A
B
C
D
思 路 分 析
4.在Rt⊿ABC中,∠C=90°,
AB=2AC.
求∠ A 、 ∠B 的度数.
作斜边AB边的中线
则 AD=CD= AB
∴AC=AD=CD= AB
又∵AB=2AC
∴⊿ACD是等边三角形
∴∠A=60°
∴∠B=30 °
练一练
(选做)已知:在Rt△ABC中,∠ABC=900,BO是AC上
的中线.求证: BO = AC
O
C
B
A
D
(友情提示)延长BO至D,使OD=BO,分别连AD、DC.
2、 如图(1):已知:在矩形ABCD中,对角线AC与BD相交于o,∠ ACB=30°,AB=5㎝,则AC= ㎝,BD= ㎝
o
C
B
A
┓
图(1)
D
作业: 1、课本p102 第4题
2、已知:如图BE、CF是△ABC的两条高,M为BC的中点,分别连ME、MF
求证: (1)ME= BC (2)ME=MF
C
M
A
B
F
E
操练场
可以明智的运用知识,再现你的魅力!
有一个角是直角的平行四边形
矩形的定义:有一个角是直角的平行四边形叫做矩形。
画出一个矩形
大胆说出
展现自我
矩形是特殊的平行四边形,猜想它有哪些性质?
作为特殊的平行四边形,矩形具有平行四边形的所有性质外,猜想还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
矩形是轴对称图形.
A
B
C
D
1:矩形的四个角都是直角
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
证明:∵矩形ABCD是平行四边形, ∠B=90°
∴ ∠B+∠C=180 °
∴∠C=90°
同理:∠D=90° ,∠A=90°
∴∠A=∠B=∠C=∠D=90°
命题
性质
已知:四边形ABCD是矩形,求证: AC = BD
A
B
C
D
证明:在矩形ABCD中
有∠ABC = ∠DAB = 90°
BC = AD
又∵AB = BA
∴△ABC≌△BAD
∴AC = BD
2:矩形的对角线相等.
命题
性质
边 角 对角线 对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
O
这是矩形所特有的性质
边
对角线
角
A
B
C
D
O
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且平分;
直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半.
O
D
C
B
A
┛
在Rt△ABD中,AO是斜边BD的中线
直角三角形的性质 :
直角三角形斜边上的中线等于斜边的一半。
则有:AO= BD
问题:矩形ABCD中,对角线AC、BD相交于点O.(1)图中有哪些相等的线段 (2)图中有哪些特殊形状的三角形
试试:用文字叙述
直角三角形的性质
在矩形ABCD中
AO=CO=BO=DO= AC= BD
例: 如图,矩形ABCD的两条对角线相交于点O, AB=4㎝,求矩形对角线的长?
解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)
D
C
B
A
O
已知对角线长是8cm,两对角线的一个夹角∠AOD是120°, 求矩形的宽AB与长BC的长.
变式:
小结:如果矩形两对角
线的夹角是60°或120°,
则其中必有等边三角形.
60°
4
∠AOB=60°,
AD = cm ,
1.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直
A
D
练一练
练一练
D
C
B
A
┓
3. 已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线.
(1)若BD=3㎝,则AC=______ ㎝;
(2)若∠C=30°,AB=5㎝,则AC=_____㎝,
BD=_____㎝.
6
5
10
A
B
C
D
思 路 分 析
4.在Rt⊿ABC中,∠C=90°,
AB=2AC.
求∠ A 、 ∠B 的度数.
作斜边AB边的中线
则 AD=CD= AB
∴AC=AD=CD= AB
又∵AB=2AC
∴⊿ACD是等边三角形
∴∠A=60°
∴∠B=30 °
练一练
(选做)已知:在Rt△ABC中,∠ABC=900,BO是AC上
的中线.求证: BO = AC
O
C
B
A
D
(友情提示)延长BO至D,使OD=BO,分别连AD、DC.
2、 如图(1):已知:在矩形ABCD中,对角线AC与BD相交于o,∠ ACB=30°,AB=5㎝,则AC= ㎝,BD= ㎝
o
C
B
A
┓
图(1)
D
作业: 1、课本p102 第4题
2、已知:如图BE、CF是△ABC的两条高,M为BC的中点,分别连ME、MF
求证: (1)ME= BC (2)ME=MF
C
M
A
B
F
E
操练场
可以明智的运用知识,再现你的魅力!
