人教版数学八年级下册19.1 函数 课时巩固练习含答案
文档属性
| 名称 | 人教版数学八年级下册19.1 函数 课时巩固练习含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 561.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-05 00:00:00 | ||
图片预览




文档简介
19.1 函 数
课时巩固练习(含答案)
一、选择题
1.一个长方形的面积是10
cm2,其长是a
cm,宽是b
cm,下列判断错误的是(
)
A.10是常量
B.10是变量
C.b是变量
D.a是变量
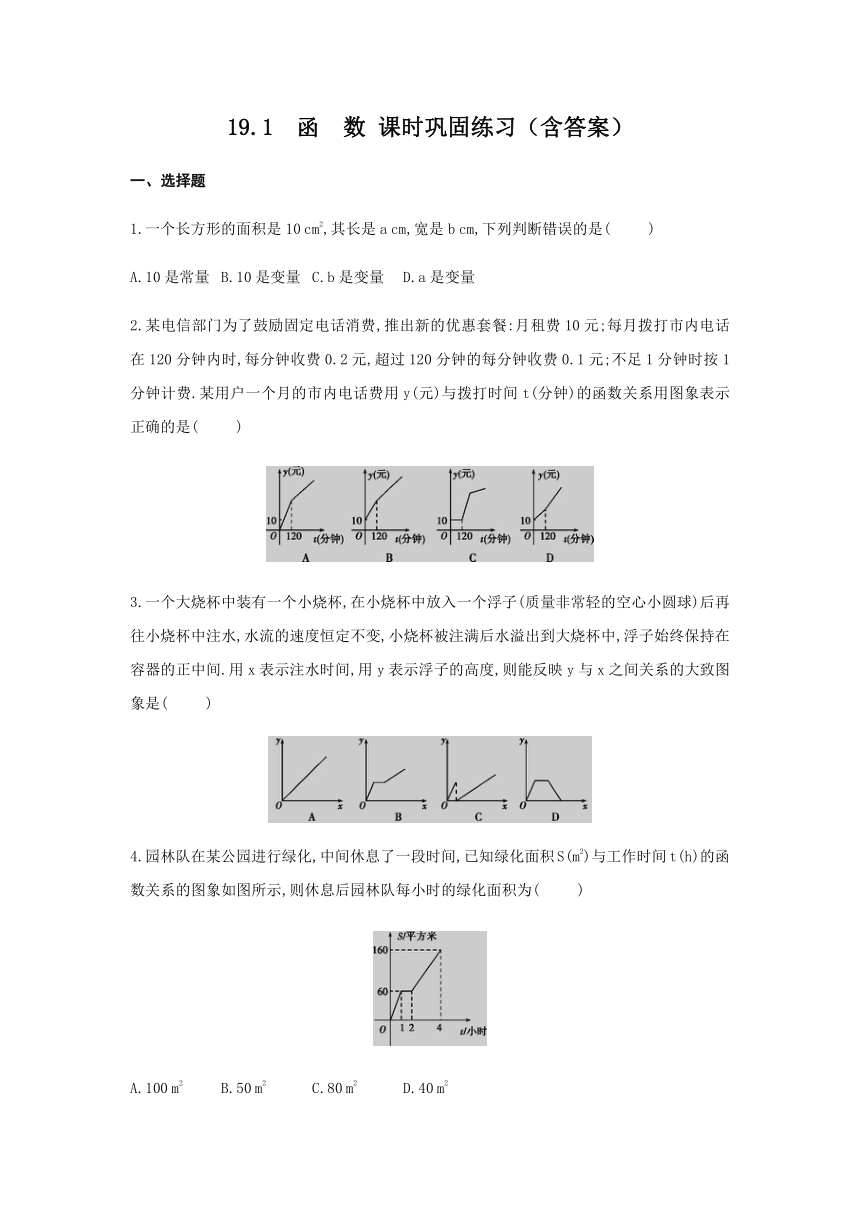
2.某电信部门为了鼓励固定电话消费,推出新的优惠套餐:月租费10元;每月拨打市内电话在120分钟内时,每分钟收费0.2元,超过120分钟的每分钟收费0.1元;不足1分钟时按1分钟计费.某用户一个月的市内电话费用y(元)与拨打时间t(分钟)的函数关系用图象表示正确的是(
)
3.一个大烧杯中装有一个小烧杯,在小烧杯中放入一个浮子(质量非常轻的空心小圆球)后再往小烧杯中注水,水流的速度恒定不变,小烧杯被注满后水溢出到大烧杯中,浮子始终保持在容器的正中间.用x表示注水时间,用y表示浮子的高度,则能反映y与x之间关系的大致图象是(
)
4.园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图所示,则休息后园林队每小时的绿化面积为(
)
A.100
m2
B.50
m2
C.80
m2
D.40
m2
5.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)之间有下面的关系,下列说法不正确的是(
)
x/kg
0
1
2
3
4
5
y/cm
20
20.5
21
21.5
22
22.5
A.弹簧不挂重物时的长度为0
cm
B.x与y都是变量,且x是自变量,y是因变量
C.物体质量每增加1
kg,弹簧长度y增加0.5
cm
D.所挂物体质量为7
kg时,弹簧长度为23.5
cm
6.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)有下面的关系:
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法不正确的是(
)
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0
cm
C.物体质量每增加1
kg,弹簧长度增加0.5
cm
D.所挂物体质量为7
kg时,弹簧长度为13.5
cm
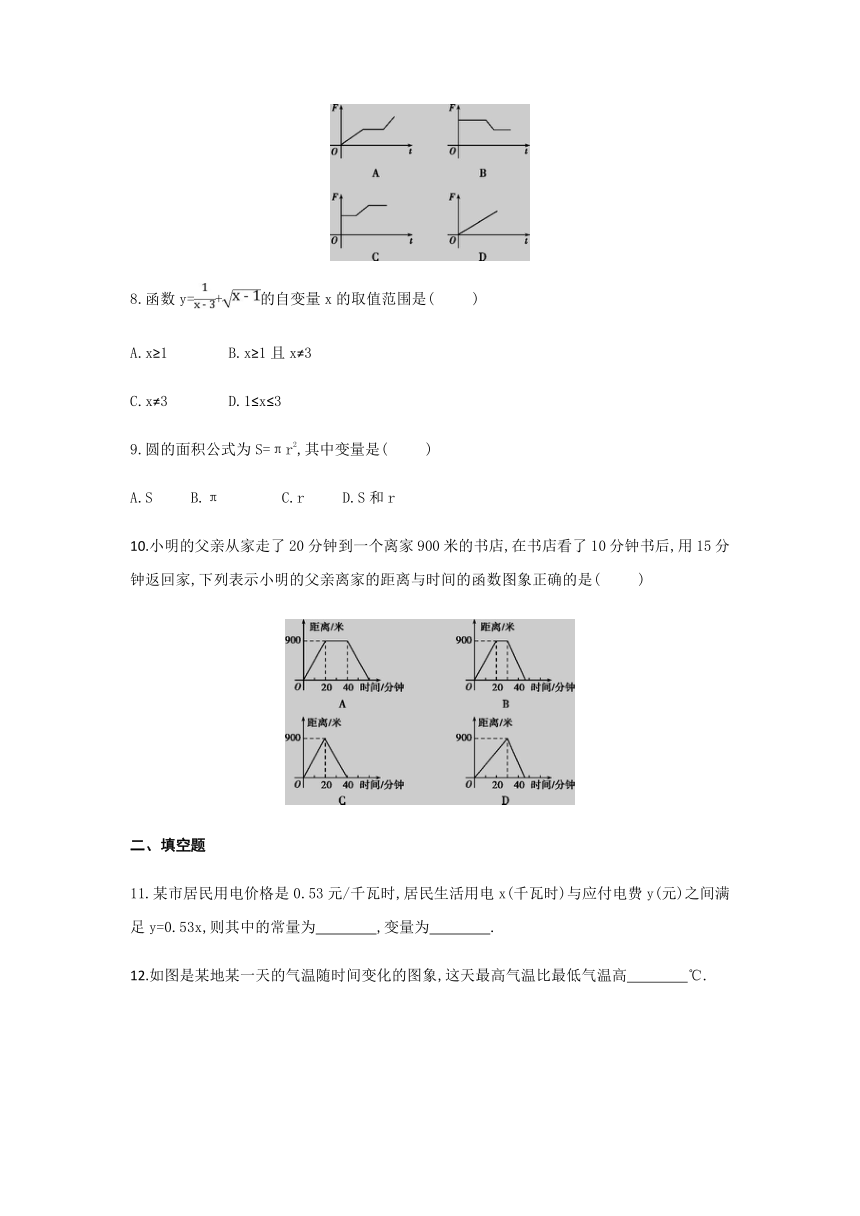
7.如图,挂在弹簧秤上的长方体铁块浸没在水中,提着弹簧秤匀速上移,直至铁块浮出水面停留在空气中(不计空气阻力),弹簧秤的读数F(N)与时间t(s)的函数图象大致是(
)
8.函数y=+的自变量x的取值范围是(
)
A.x≥1 B.x≥1且x≠3
C.x≠3 D.1≤x≤3
9.圆的面积公式为S=πr2,其中变量是(
)
A.S
B.π
C.r
D.S和r
10.小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列表示小明的父亲离家的距离与时间的函数图象正确的是(
)
二、填空题
11.某市居民用电价格是0.53元/千瓦时,居民生活用电x(千瓦时)与应付电费y(元)之间满足y=0.53x,则其中的常量为 ,变量为 .?
12.如图是某地某一天的气温随时间变化的图象,这天最高气温比最低气温高 ℃.?
13.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动,图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶 千米.?
14.在函数y=+x-2中,自变量x的取值范围是 .?
15.据测试,拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小明洗手后没有把水龙头拧紧,水龙头以测试速度滴水,当小明离开x分钟后,水龙头滴水y毫升,则y与x之间的函数关系式是 .?
16.如果整数x>-3,那么使得函数y=有意义的x的值是 .?
三、解答题
17.下表是某报纸公布的世界人口数据情况:
年份
1957
1974
1987
1999
2010
2025
世界人口总数
30亿
40亿
50亿
60亿
70亿
80亿
(1)表中有几个变量?
(2)如果要用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是怎样的?
18.为研究某地的高度h(千米)与温度t(℃)之间的关系,某天研究人员在该地的不同高度处同时进行了若干次测量,测得的数据如下:
h(千米)
0
0.5
1
1.5
2
2.5
3
t(℃)
25
22
19
16
13
10
7
(1)写出h与t之间的一个关系式;
(2)估计3.5千米高度处的温度.
20.李大爷按每千克2.1元批发了一批蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)李大爷自带的零钱是 元;?
(2)降价前每千克蜜橘出售的价格是 元/千克;?
(3)卖了几天,蜜橘卖相不好了,随后他按每千克下降1.5元将剩下的蜜橘售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克蜜橘?
21.如图,矩形ABCD中,当点P在边AD(不包括A,D两点)上从A向D移动时,有些线段的长度和三角形的面积始终保持不变,而有些发生了变化.
(1)试分别写出长度发生变化的线段与面积发生变化的三角形;
(2)假设矩形的长AD为10
cm,宽AB为4
cm,线段AP的长为x
cm,分别写出线段PD的长度y(cm)、△PCD的面积S(cm2)与x之间的函数解析式,并指出自变量的取值范围.
参考答案:
一、选择题
1.一个长方形的面积是10
cm2,其长是a
cm,宽是b
cm,下列判断错误的是( B )
A.10是常量
B.10是变量
C.b是变量
D.a是变量
2.某电信部门为了鼓励固定电话消费,推出新的优惠套餐:月租费10元;每月拨打市内电话在120分钟内时,每分钟收费0.2元,超过120分钟的每分钟收费0.1元;不足1分钟时按1分钟计费.某用户一个月的市内电话费用y(元)与拨打时间t(分钟)的函数关系用图象表示正确的是( B )
3.一个大烧杯中装有一个小烧杯,在小烧杯中放入一个浮子(质量非常轻的空心小圆球)后再往小烧杯中注水,水流的速度恒定不变,小烧杯被注满后水溢出到大烧杯中,浮子始终保持在容器的正中间.用x表示注水时间,用y表示浮子的高度,则能反映y与x之间关系的大致图象是( B )
4.园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图所示,则休息后园林队每小时的绿化面积为( B )
A.100
m2
B.50
m2
C.80
m2
D.40
m2
5.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)之间有下面的关系,下列说法不正确的是( A )
x/kg
0
1
2
3
4
5
y/cm
20
20.5
21
21.5
22
22.5
A.弹簧不挂重物时的长度为0
cm
B.x与y都是变量,且x是自变量,y是因变量
C.物体质量每增加1
kg,弹簧长度y增加0.5
cm
D.所挂物体质量为7
kg时,弹簧长度为23.5
cm
6.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)有下面的关系:
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法不正确的是( B )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0
cm
C.物体质量每增加1
kg,弹簧长度增加0.5
cm
D.所挂物体质量为7
kg时,弹簧长度为13.5
cm
7.如图,挂在弹簧秤上的长方体铁块浸没在水中,提着弹簧秤匀速上移,直至铁块浮出水面停留在空气中(不计空气阻力),弹簧秤的读数F(N)与时间t(s)的函数图象大致是( C )
8.函数y=+的自变量x的取值范围是( B )
A.x≥1 B.x≥1且x≠3
C.x≠3 D.1≤x≤3
9.圆的面积公式为S=πr2,其中变量是( D )
A.S
B.π
C.r
D.S和r
10.小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列表示小明的父亲离家的距离与时间的函数图象正确的是( B )
二、填空题
11.某市居民用电价格是0.53元/千瓦时,居民生活用电x(千瓦时)与应付电费y(元)之间满足y=0.53x,则其中的常量为 ,变量为 .?
答案 0.53;x,y
12.如图是某地某一天的气温随时间变化的图象,这天最高气温比最低气温高 ℃.?
答案 12
13.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动,图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶 千米.?
答案
14.在函数y=+x-2中,自变量x的取值范围是 .?
答案 x≥-4且x≠0
15.据测试,拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小明洗手后没有把水龙头拧紧,水龙头以测试速度滴水,当小明离开x分钟后,水龙头滴水y毫升,则y与x之间的函数关系式是 .?
答案 y=5x
16.如果整数x>-3,那么使得函数y=有意义的x的值是 .?
答案 -2、-1、0、1
三、解答题
17.下表是某报纸公布的世界人口数据情况:
年份
1957
1974
1987
1999
2010
2025
世界人口总数
30亿
40亿
50亿
60亿
70亿
80亿
(1)表中有几个变量?
(2)如果要用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是怎样的?
解析 (1)表中有两个变量,分别是年份和世界人口总数.
(2)用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是增大.
18.为研究某地的高度h(千米)与温度t(℃)之间的关系,某天研究人员在该地的不同高度处同时进行了若干次测量,测得的数据如下:
h(千米)
0
0.5
1
1.5
2
2.5
3
t(℃)
25
22
19
16
13
10
7
(1)写出h与t之间的一个关系式;
(2)估计3.5千米高度处的温度.
解析 (1)通过比较变量之间的数量关系,可以发现:温度=25-6×高度,即t=25-6h.
(2)当h=3.5时,t=25-6h=25-6×3.5=4.即3.5千米高度处的温度为4
℃.
20.李大爷按每千克2.1元批发了一批蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)李大爷自带的零钱是 元;?
(2)降价前每千克蜜橘出售的价格是 元/千克;?
(3)卖了几天,蜜橘卖相不好了,随后他按每千克下降1.5元将剩下的蜜橘售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克蜜橘?
解析 (1)当x=0时,y=50.故答案为50.
(2)降价前的售价为(330-50)÷80==3.5(元/千克).故答案为3.5.
(3)李大爷一共批发的蜜橘质量为80+(450-330)÷(3.5-1.5)=140(千克).
答:李大爷一共批发了140千克蜜橘.
21.如图,矩形ABCD中,当点P在边AD(不包括A,D两点)上从A向D移动时,有些线段的长度和三角形的面积始终保持不变,而有些发生了变化.
(1)试分别写出长度发生变化的线段与面积发生变化的三角形;
(2)假设矩形的长AD为10
cm,宽AB为4
cm,线段AP的长为x
cm,分别写出线段PD的长度y(cm)、△PCD的面积S(cm2)与x之间的函数解析式,并指出自变量的取值范围.
解析 (1)长度发生变化的线段:AP,PD,BP,PC;面积发生变化的三角形:△APB、△DCP.
(2)根据题意可知PD=AD-AP,因为AD=10
cm,AP=x
cm,所以y=10-x.其中0
课时巩固练习(含答案)
一、选择题
1.一个长方形的面积是10
cm2,其长是a
cm,宽是b
cm,下列判断错误的是(
)
A.10是常量
B.10是变量
C.b是变量
D.a是变量
2.某电信部门为了鼓励固定电话消费,推出新的优惠套餐:月租费10元;每月拨打市内电话在120分钟内时,每分钟收费0.2元,超过120分钟的每分钟收费0.1元;不足1分钟时按1分钟计费.某用户一个月的市内电话费用y(元)与拨打时间t(分钟)的函数关系用图象表示正确的是(
)
3.一个大烧杯中装有一个小烧杯,在小烧杯中放入一个浮子(质量非常轻的空心小圆球)后再往小烧杯中注水,水流的速度恒定不变,小烧杯被注满后水溢出到大烧杯中,浮子始终保持在容器的正中间.用x表示注水时间,用y表示浮子的高度,则能反映y与x之间关系的大致图象是(
)
4.园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图所示,则休息后园林队每小时的绿化面积为(
)
A.100
m2
B.50
m2
C.80
m2
D.40
m2
5.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)之间有下面的关系,下列说法不正确的是(
)
x/kg
0
1
2
3
4
5
y/cm
20
20.5
21
21.5
22
22.5
A.弹簧不挂重物时的长度为0
cm
B.x与y都是变量,且x是自变量,y是因变量
C.物体质量每增加1
kg,弹簧长度y增加0.5
cm
D.所挂物体质量为7
kg时,弹簧长度为23.5
cm
6.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)有下面的关系:
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法不正确的是(
)
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0
cm
C.物体质量每增加1
kg,弹簧长度增加0.5
cm
D.所挂物体质量为7
kg时,弹簧长度为13.5
cm
7.如图,挂在弹簧秤上的长方体铁块浸没在水中,提着弹簧秤匀速上移,直至铁块浮出水面停留在空气中(不计空气阻力),弹簧秤的读数F(N)与时间t(s)的函数图象大致是(
)
8.函数y=+的自变量x的取值范围是(
)
A.x≥1 B.x≥1且x≠3
C.x≠3 D.1≤x≤3
9.圆的面积公式为S=πr2,其中变量是(
)
A.S
B.π
C.r
D.S和r
10.小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列表示小明的父亲离家的距离与时间的函数图象正确的是(
)
二、填空题
11.某市居民用电价格是0.53元/千瓦时,居民生活用电x(千瓦时)与应付电费y(元)之间满足y=0.53x,则其中的常量为 ,变量为 .?
12.如图是某地某一天的气温随时间变化的图象,这天最高气温比最低气温高 ℃.?
13.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动,图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶 千米.?
14.在函数y=+x-2中,自变量x的取值范围是 .?
15.据测试,拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小明洗手后没有把水龙头拧紧,水龙头以测试速度滴水,当小明离开x分钟后,水龙头滴水y毫升,则y与x之间的函数关系式是 .?
16.如果整数x>-3,那么使得函数y=有意义的x的值是 .?
三、解答题
17.下表是某报纸公布的世界人口数据情况:
年份
1957
1974
1987
1999
2010
2025
世界人口总数
30亿
40亿
50亿
60亿
70亿
80亿
(1)表中有几个变量?
(2)如果要用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是怎样的?
18.为研究某地的高度h(千米)与温度t(℃)之间的关系,某天研究人员在该地的不同高度处同时进行了若干次测量,测得的数据如下:
h(千米)
0
0.5
1
1.5
2
2.5
3
t(℃)
25
22
19
16
13
10
7
(1)写出h与t之间的一个关系式;
(2)估计3.5千米高度处的温度.
20.李大爷按每千克2.1元批发了一批蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)李大爷自带的零钱是 元;?
(2)降价前每千克蜜橘出售的价格是 元/千克;?
(3)卖了几天,蜜橘卖相不好了,随后他按每千克下降1.5元将剩下的蜜橘售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克蜜橘?
21.如图,矩形ABCD中,当点P在边AD(不包括A,D两点)上从A向D移动时,有些线段的长度和三角形的面积始终保持不变,而有些发生了变化.
(1)试分别写出长度发生变化的线段与面积发生变化的三角形;
(2)假设矩形的长AD为10
cm,宽AB为4
cm,线段AP的长为x
cm,分别写出线段PD的长度y(cm)、△PCD的面积S(cm2)与x之间的函数解析式,并指出自变量的取值范围.
参考答案:
一、选择题
1.一个长方形的面积是10
cm2,其长是a
cm,宽是b
cm,下列判断错误的是( B )
A.10是常量
B.10是变量
C.b是变量
D.a是变量
2.某电信部门为了鼓励固定电话消费,推出新的优惠套餐:月租费10元;每月拨打市内电话在120分钟内时,每分钟收费0.2元,超过120分钟的每分钟收费0.1元;不足1分钟时按1分钟计费.某用户一个月的市内电话费用y(元)与拨打时间t(分钟)的函数关系用图象表示正确的是( B )
3.一个大烧杯中装有一个小烧杯,在小烧杯中放入一个浮子(质量非常轻的空心小圆球)后再往小烧杯中注水,水流的速度恒定不变,小烧杯被注满后水溢出到大烧杯中,浮子始终保持在容器的正中间.用x表示注水时间,用y表示浮子的高度,则能反映y与x之间关系的大致图象是( B )
4.园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图所示,则休息后园林队每小时的绿化面积为( B )
A.100
m2
B.50
m2
C.80
m2
D.40
m2
5.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)之间有下面的关系,下列说法不正确的是( A )
x/kg
0
1
2
3
4
5
y/cm
20
20.5
21
21.5
22
22.5
A.弹簧不挂重物时的长度为0
cm
B.x与y都是变量,且x是自变量,y是因变量
C.物体质量每增加1
kg,弹簧长度y增加0.5
cm
D.所挂物体质量为7
kg时,弹簧长度为23.5
cm
6.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)有下面的关系:
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
下列说法不正确的是( B )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0
cm
C.物体质量每增加1
kg,弹簧长度增加0.5
cm
D.所挂物体质量为7
kg时,弹簧长度为13.5
cm
7.如图,挂在弹簧秤上的长方体铁块浸没在水中,提着弹簧秤匀速上移,直至铁块浮出水面停留在空气中(不计空气阻力),弹簧秤的读数F(N)与时间t(s)的函数图象大致是( C )
8.函数y=+的自变量x的取值范围是( B )
A.x≥1 B.x≥1且x≠3
C.x≠3 D.1≤x≤3
9.圆的面积公式为S=πr2,其中变量是( D )
A.S
B.π
C.r
D.S和r
10.小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列表示小明的父亲离家的距离与时间的函数图象正确的是( B )
二、填空题
11.某市居民用电价格是0.53元/千瓦时,居民生活用电x(千瓦时)与应付电费y(元)之间满足y=0.53x,则其中的常量为 ,变量为 .?
答案 0.53;x,y
12.如图是某地某一天的气温随时间变化的图象,这天最高气温比最低气温高 ℃.?
答案 12
13.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动,图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶 千米.?
答案
14.在函数y=+x-2中,自变量x的取值范围是 .?
答案 x≥-4且x≠0
15.据测试,拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小明洗手后没有把水龙头拧紧,水龙头以测试速度滴水,当小明离开x分钟后,水龙头滴水y毫升,则y与x之间的函数关系式是 .?
答案 y=5x
16.如果整数x>-3,那么使得函数y=有意义的x的值是 .?
答案 -2、-1、0、1
三、解答题
17.下表是某报纸公布的世界人口数据情况:
年份
1957
1974
1987
1999
2010
2025
世界人口总数
30亿
40亿
50亿
60亿
70亿
80亿
(1)表中有几个变量?
(2)如果要用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是怎样的?
解析 (1)表中有两个变量,分别是年份和世界人口总数.
(2)用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是增大.
18.为研究某地的高度h(千米)与温度t(℃)之间的关系,某天研究人员在该地的不同高度处同时进行了若干次测量,测得的数据如下:
h(千米)
0
0.5
1
1.5
2
2.5
3
t(℃)
25
22
19
16
13
10
7
(1)写出h与t之间的一个关系式;
(2)估计3.5千米高度处的温度.
解析 (1)通过比较变量之间的数量关系,可以发现:温度=25-6×高度,即t=25-6h.
(2)当h=3.5时,t=25-6h=25-6×3.5=4.即3.5千米高度处的温度为4
℃.
20.李大爷按每千克2.1元批发了一批蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)李大爷自带的零钱是 元;?
(2)降价前每千克蜜橘出售的价格是 元/千克;?
(3)卖了几天,蜜橘卖相不好了,随后他按每千克下降1.5元将剩下的蜜橘售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克蜜橘?
解析 (1)当x=0时,y=50.故答案为50.
(2)降价前的售价为(330-50)÷80==3.5(元/千克).故答案为3.5.
(3)李大爷一共批发的蜜橘质量为80+(450-330)÷(3.5-1.5)=140(千克).
答:李大爷一共批发了140千克蜜橘.
21.如图,矩形ABCD中,当点P在边AD(不包括A,D两点)上从A向D移动时,有些线段的长度和三角形的面积始终保持不变,而有些发生了变化.
(1)试分别写出长度发生变化的线段与面积发生变化的三角形;
(2)假设矩形的长AD为10
cm,宽AB为4
cm,线段AP的长为x
cm,分别写出线段PD的长度y(cm)、△PCD的面积S(cm2)与x之间的函数解析式,并指出自变量的取值范围.
解析 (1)长度发生变化的线段:AP,PD,BP,PC;面积发生变化的三角形:△APB、△DCP.
(2)根据题意可知PD=AD-AP,因为AD=10
cm,AP=x
cm,所以y=10-x.其中0
