湘教版七年级数学下册 2.2.1平方差公式课件(共21张PPT)
文档属性
| 名称 | 湘教版七年级数学下册 2.2.1平方差公式课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-04 15:41:50 | ||
图片预览







文档简介
(共21张PPT)
2.2.1
平方差公式
湘教版
七年级下册
1.理解并掌握平方差公式的推导和应用.(重点)
2.理解平方差公式的结构特征,并能运用公式进行简
单的运算.(难点)
学习目标
1、多项式乘多项式法则
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn
2、两项式乘以两项式,结果可能是两项吗?
请你举例说明.
计算下列各式,你能发现什么规律:
(a
+
2
)(
a
–
2)
=
a2-
2a
+
2a
-
22=
,
(a
+
1
)(
a
-
1)
=
a2-
a
+
a
-
12=
,
(a
+
3
)(
a
-
3)
=
a2-
3a
+
3a
-32=
,
(a
+
4
)(
a
-
4
)
=
a2-
4a
+
4a
-42=
.
a2-
12
a2-
22
a2-
32
a2-42
(-a
+
1
)(
-a
-
1)
=
a2+a
-a
-
12=
,
(-a
+
2
)(
-a
–
2)
=
a2+2a
-2a
-
22=
,
(-a
+
3
)(
-a
-
3)
=
a2+3a
-
3a
-32=
,
(-a
+
4
)(
-a
-
4
)
=
a2+
4a
-
4a
-42=
.
平
方
差
公
式
(1)
(x+3)(x?3)
;
(2)
(1+2a)(1?2a)
;
(3)
(x+4y)(x?4y)
;
(4)
(y+5z)(y?5z)
;
=x2?9
;
=1?4a2
;
=x2?16y2
;
=y2?25z2
;
你发现了什么规律?
用自己的语言叙述你的发现.
=x2?32
;
=12?(2a)2
;
=x2?(4y)2
;
=y2?(5z)2
.
(a+b)(a?b)=
a2?b2.
两数和与这两数差的积,
等于
这两数的平方的差.
用式子表示,即:
(a+b)(a?b)=a2?b2.
两数和与这两数差的积,等于它们的平方差
对于不符合平方差公式标准形式者,或提取两“?”号中的“?”号,要利用加法交换律,变成公式标准形式后,再用公式.
平方差公式
抽象归纳
公式特征:
使用公式应该注意:
相乘的两个括号中有一对相同的数(式子),
有一对互为相反数的数(式子)
找清哪个是相同的,即公式中的a;
哪个是互为相反数的,即公式中的b
平方差公式对我们的帮助:
可以使我们在计算这种类型的多项式乘法时
直接用公式更加快速和简便
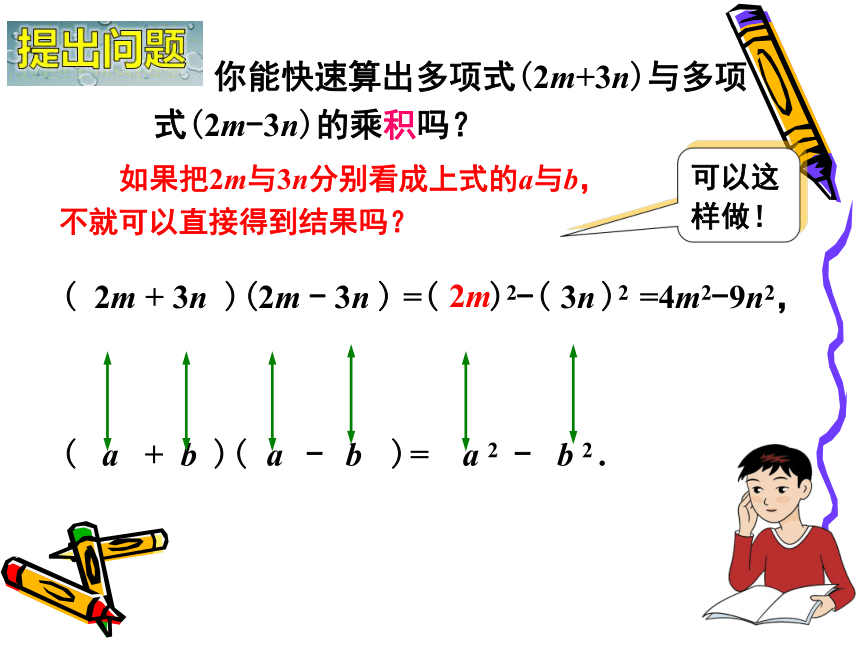
你能快速算出多项式(2m+3n)与多项式(2m-3n)的乘积吗?
可以这样做!
如果把2m与3n分别看成上式的a与b,
不就可以直接得到结果吗?
(
2m
+
3n
)(2m
-
3n
)
(
+
)(
-
)
a
b
a
b
=
a
2
-
b
2
.
=(
)2-(
)2
2m
3n
=4m2-9n2,
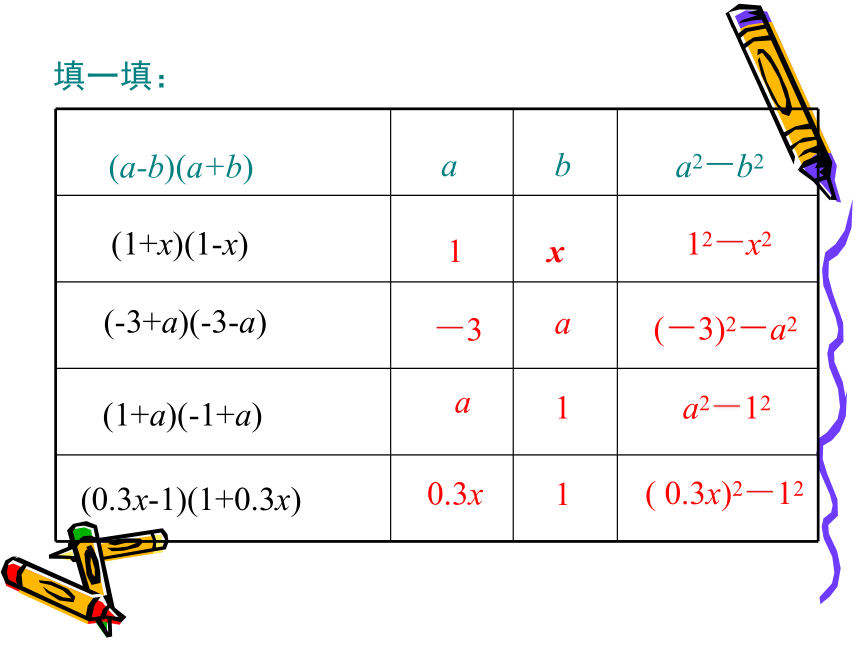
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
填一填:
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
(
0.3x)2-12
(a-b)(a+b)
口答下列各题:
(l)(-a+b)(a+b)=??_________
(2)(a-b)(b+a)=
__________
(3)(-a-b)(-a+b)=
________
(4)(a-b)(-a-b)=
_________
a2-b2
a2-b2
b2-a2
b2-a2
例1、用平方差公式计算
(1)(2x+1)(2x-1)
解:原式=
(2x)2
-12
=4x2
-
1
1、先把要计算的式子与公式对照,
2、哪个是
a
,哪个是
b.
(2)(x+2y)(x-2y)
原式=x2
-(2y)2
=x2
–
4y2
(2)(4a+b)(-b+4a).
解:(4a+b)(-b+4a)
=
(4a)2
-b2
=
16a2
-b2
例2
运用平方差公式计算:
1002×998
(1)1002×998
=(1000
+2)
×(1000-2
)
=10002
?22
=1000000?4
=9999996
例3
计算:
解:
1.
下面各式的计算对不对?如果不对,应怎样改正
?
(1)(x-2)(x+2)=x2-2;
(2)(-2x-1)(2x-1)=4x2-1;
不对,应是:x2-4.
不对.
应是:1-4x2
(6)(x-2)(-x+2)=x2-4.
不对.
不能用平方差公式计算。
(3)
(1+2x)(1?2x)=1?2x2
;
(4)
(2a2+b2)(2a2?b2)=2a4?b4;
(5)
(3m+2n)(3m?2n)=3m2?2n2;
本题对公式的直接运用,以加深对公式本质特征的理解
不对.
应是:1-4x2
不对,应是:4a4-b4.
不对,应是:9m2-4n2.
变式训练
下列式子能平方差公式计算吗?
为什么?
如果能够,怎样计算?
(1)
(a+b)(?a?b)
;
(2)
(a?b)(b?a)
;
(3)
(a+2b)(2b+a);
(4)
?(a?b)(a+b)
;
(5)
(?2x+y)(y?2x).
(不能)
(不能)
(不能)
(能)
(不能)
(第一个数不完全一样
)
?(a2
?b2)=
?a2
+
b2
;
本题是公式的变式训练,以加深对公式本质特征的理解
2.
运用平方差公式计算:
(1)(3a+b)(3a-b);
(2)(m+2n)(m-2n);
(4)(-1+5a)(-1-5a).
(3)
=
9a2-b2
=
m2-4n2
=
1-25a2.
3、用公式计算:
1
002
×
998
.
答案:
999
996
202×198;
49.8×50.2
.
答案:39
996
答案:2
499.96
运算练习1
(5)
(5a
+3b)(5a?3b)
;
(6)
(?4k+3)(?4k?3)
.
=
25a2-9b2
=
16k2-9
=
x2-y2
1.下列多项式乘法,能用平方差公式进行计算的是(
)
A.
(x+y)(-x-y)
B.
(2x+3y)(2x-3z)
C.
(-a-b)(a-b)
D.
(m-n)(n-m)
C
2.下列计算正确的是(
)
A.
(2x+3)(2x-3)=2x2-9
B.
(x+4)(x-4)=x2-4
C.
(5+x)(x-6)=x2-30
D.
(-1+4b)(-1-4b)=1-16b2
D
3.
(4x2-5y)需乘以下列哪个式子,才能使用平方差公式进行计算(
)
A.
-4x2-5y
B.
-4x2+5y
C.
(4x2-5y)2
D.
(4x+5y)2
A
运算练习2
4.
a4+(1-a)(1+a)(1+a2)的计算结果是(
)
A.
-1
B.
1
C.
2a4-1
D.
1-2a4
B
D
5、下列式子能用平方差公式计算的有(
)
A.
1个
B.2个
C.
3个
D.
4个
(1)
(2)
(3)
(4)
2.若A=(2+1)(22+1)(24+1),则A的值是______.
解析:A=(2+1)(22+1)(24+1)
=[(2-1)(2+1)(22+1)(24+1)]÷(2-1)
=[(22-1)(22+1)(24+1)]÷(2-1)
=[(24-1)(24+1)]÷(2-1)
=(28-1)÷(2-1)
=28-1.
28-1
能力拓展:
1.(x-y)(x+y)(x2+y2);
解:原式=(x2-y2)(x2+y2)=x4-y4;
课堂小结
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.紧紧抓住
“一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
谢谢,请提出宝贵意见!
2.2.1
平方差公式
湘教版
七年级下册
1.理解并掌握平方差公式的推导和应用.(重点)
2.理解平方差公式的结构特征,并能运用公式进行简
单的运算.(难点)
学习目标
1、多项式乘多项式法则
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn
2、两项式乘以两项式,结果可能是两项吗?
请你举例说明.
计算下列各式,你能发现什么规律:
(a
+
2
)(
a
–
2)
=
a2-
2a
+
2a
-
22=
,
(a
+
1
)(
a
-
1)
=
a2-
a
+
a
-
12=
,
(a
+
3
)(
a
-
3)
=
a2-
3a
+
3a
-32=
,
(a
+
4
)(
a
-
4
)
=
a2-
4a
+
4a
-42=
.
a2-
12
a2-
22
a2-
32
a2-42
(-a
+
1
)(
-a
-
1)
=
a2+a
-a
-
12=
,
(-a
+
2
)(
-a
–
2)
=
a2+2a
-2a
-
22=
,
(-a
+
3
)(
-a
-
3)
=
a2+3a
-
3a
-32=
,
(-a
+
4
)(
-a
-
4
)
=
a2+
4a
-
4a
-42=
.
平
方
差
公
式
(1)
(x+3)(x?3)
;
(2)
(1+2a)(1?2a)
;
(3)
(x+4y)(x?4y)
;
(4)
(y+5z)(y?5z)
;
=x2?9
;
=1?4a2
;
=x2?16y2
;
=y2?25z2
;
你发现了什么规律?
用自己的语言叙述你的发现.
=x2?32
;
=12?(2a)2
;
=x2?(4y)2
;
=y2?(5z)2
.
(a+b)(a?b)=
a2?b2.
两数和与这两数差的积,
等于
这两数的平方的差.
用式子表示,即:
(a+b)(a?b)=a2?b2.
两数和与这两数差的积,等于它们的平方差
对于不符合平方差公式标准形式者,或提取两“?”号中的“?”号,要利用加法交换律,变成公式标准形式后,再用公式.
平方差公式
抽象归纳
公式特征:
使用公式应该注意:
相乘的两个括号中有一对相同的数(式子),
有一对互为相反数的数(式子)
找清哪个是相同的,即公式中的a;
哪个是互为相反数的,即公式中的b
平方差公式对我们的帮助:
可以使我们在计算这种类型的多项式乘法时
直接用公式更加快速和简便
你能快速算出多项式(2m+3n)与多项式(2m-3n)的乘积吗?
可以这样做!
如果把2m与3n分别看成上式的a与b,
不就可以直接得到结果吗?
(
2m
+
3n
)(2m
-
3n
)
(
+
)(
-
)
a
b
a
b
=
a
2
-
b
2
.
=(
)2-(
)2
2m
3n
=4m2-9n2,
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
填一填:
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
(
0.3x)2-12
(a-b)(a+b)
口答下列各题:
(l)(-a+b)(a+b)=??_________
(2)(a-b)(b+a)=
__________
(3)(-a-b)(-a+b)=
________
(4)(a-b)(-a-b)=
_________
a2-b2
a2-b2
b2-a2
b2-a2
例1、用平方差公式计算
(1)(2x+1)(2x-1)
解:原式=
(2x)2
-12
=4x2
-
1
1、先把要计算的式子与公式对照,
2、哪个是
a
,哪个是
b.
(2)(x+2y)(x-2y)
原式=x2
-(2y)2
=x2
–
4y2
(2)(4a+b)(-b+4a).
解:(4a+b)(-b+4a)
=
(4a)2
-b2
=
16a2
-b2
例2
运用平方差公式计算:
1002×998
(1)1002×998
=(1000
+2)
×(1000-2
)
=10002
?22
=1000000?4
=9999996
例3
计算:
解:
1.
下面各式的计算对不对?如果不对,应怎样改正
?
(1)(x-2)(x+2)=x2-2;
(2)(-2x-1)(2x-1)=4x2-1;
不对,应是:x2-4.
不对.
应是:1-4x2
(6)(x-2)(-x+2)=x2-4.
不对.
不能用平方差公式计算。
(3)
(1+2x)(1?2x)=1?2x2
;
(4)
(2a2+b2)(2a2?b2)=2a4?b4;
(5)
(3m+2n)(3m?2n)=3m2?2n2;
本题对公式的直接运用,以加深对公式本质特征的理解
不对.
应是:1-4x2
不对,应是:4a4-b4.
不对,应是:9m2-4n2.
变式训练
下列式子能平方差公式计算吗?
为什么?
如果能够,怎样计算?
(1)
(a+b)(?a?b)
;
(2)
(a?b)(b?a)
;
(3)
(a+2b)(2b+a);
(4)
?(a?b)(a+b)
;
(5)
(?2x+y)(y?2x).
(不能)
(不能)
(不能)
(能)
(不能)
(第一个数不完全一样
)
?(a2
?b2)=
?a2
+
b2
;
本题是公式的变式训练,以加深对公式本质特征的理解
2.
运用平方差公式计算:
(1)(3a+b)(3a-b);
(2)(m+2n)(m-2n);
(4)(-1+5a)(-1-5a).
(3)
=
9a2-b2
=
m2-4n2
=
1-25a2.
3、用公式计算:
1
002
×
998
.
答案:
999
996
202×198;
49.8×50.2
.
答案:39
996
答案:2
499.96
运算练习1
(5)
(5a
+3b)(5a?3b)
;
(6)
(?4k+3)(?4k?3)
.
=
25a2-9b2
=
16k2-9
=
x2-y2
1.下列多项式乘法,能用平方差公式进行计算的是(
)
A.
(x+y)(-x-y)
B.
(2x+3y)(2x-3z)
C.
(-a-b)(a-b)
D.
(m-n)(n-m)
C
2.下列计算正确的是(
)
A.
(2x+3)(2x-3)=2x2-9
B.
(x+4)(x-4)=x2-4
C.
(5+x)(x-6)=x2-30
D.
(-1+4b)(-1-4b)=1-16b2
D
3.
(4x2-5y)需乘以下列哪个式子,才能使用平方差公式进行计算(
)
A.
-4x2-5y
B.
-4x2+5y
C.
(4x2-5y)2
D.
(4x+5y)2
A
运算练习2
4.
a4+(1-a)(1+a)(1+a2)的计算结果是(
)
A.
-1
B.
1
C.
2a4-1
D.
1-2a4
B
D
5、下列式子能用平方差公式计算的有(
)
A.
1个
B.2个
C.
3个
D.
4个
(1)
(2)
(3)
(4)
2.若A=(2+1)(22+1)(24+1),则A的值是______.
解析:A=(2+1)(22+1)(24+1)
=[(2-1)(2+1)(22+1)(24+1)]÷(2-1)
=[(22-1)(22+1)(24+1)]÷(2-1)
=[(24-1)(24+1)]÷(2-1)
=(28-1)÷(2-1)
=28-1.
28-1
能力拓展:
1.(x-y)(x+y)(x2+y2);
解:原式=(x2-y2)(x2+y2)=x4-y4;
课堂小结
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.紧紧抓住
“一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
谢谢,请提出宝贵意见!
