人教版七年级数学下册课件:8.3实际问题与二元一次方程组(共37张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:8.3实际问题与二元一次方程组(共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 209.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-04 17:34:03 | ||
图片预览










文档简介
(共37张PPT)
数学七年级下册第八章二元一次方程组
8.3
实际问题与二元一次方程组
学习目标
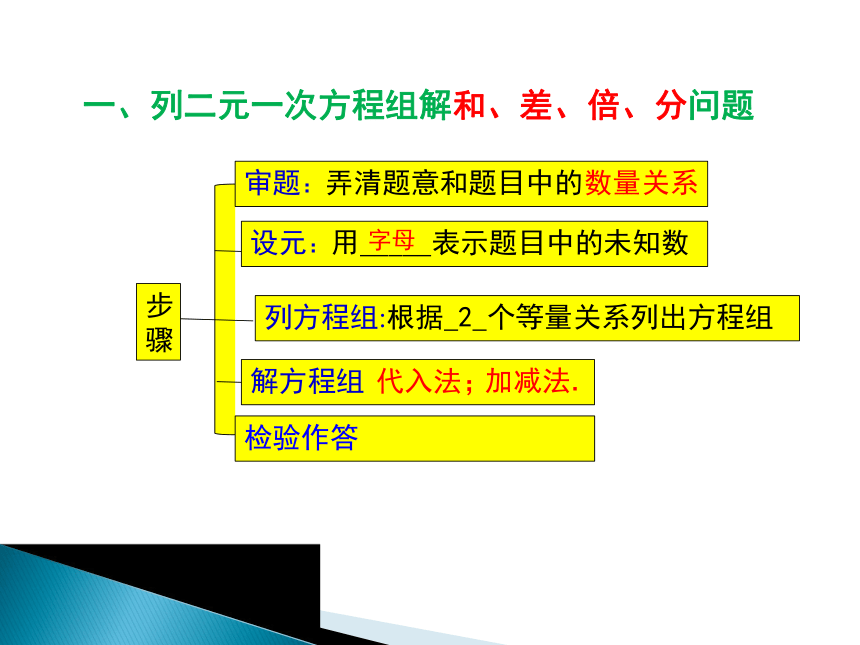
1、列二元一次方程组解和、差、倍、分问题
2、列二元一次方程组解几何问题
3、列二元一次方程组解行程与配套问题
4、列二元一次方程组解百分率问题
5、列方程组解数字、工程、计数问题
一、列二元一次方程组解和、差、倍、分问题
步骤
审题:弄清题意和题目中的
设元:用_____表示题目中的未知数
解方程组
检验作答
数量关系
字母
2
代入法;
加减法.
列方程组:根据_2_个等量关系列出方程组
例1:小明买了50分和20分的邮票共16枚,花了5元9角钱,20分和50分的邮票各买了多少枚?根据题意完成下列各题:
(1)设小明买了20分的邮票x枚,则50分的邮票买了_____________枚,由题意可得一元一次方程______________________.
(16-x)
20x+(16-x)×50=590
(2)设20分的邮票买了x枚,50分的邮票买了y枚,由题意可得二元一次方程组
(3)设买20分的邮票花了x元,买50分的邮票花了y元,由题意可得二元一次方程组
x+y=16
20x+50y=590
例2:列方程解应用题:《九章算术》中有“盈不足术”的问题,原文如下:“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”
题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元,求人数和羊价各是多少.
解:设买羊人共有x人,羊价为y元.
由题意得
,
解得
答:买羊人共有21人,羊价为150元.
y=5x+45
y=7x+3
x=21
y=150
解:
设每名熟练工人和新工人每月分别可以安装x、y辆电动汽车,根据题意,得
解之得
x+2y=8
2x+3y=14.
答:每名熟练工和新工人每月分别可以安装4辆、2辆电动汽车.
例3.某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.则每名熟练工和新工人每月分别可以安装多少辆电动汽车?
x=4
y=2.
例4:《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱.如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的
,那么乙也共有钱48文
.甲、乙两人原来各有多少钱?
解:设甲原有x文钱,乙原有y文钱,
由题意可得
解得:
答:甲原有36文钱,乙原有24文钱.
2、列二元一次方程组解几何问题
用二元一次方程组解几何图形问题时,要根据几何图形的性质、公式结合图形中反映的数量关系,建立二元一次方程组的模型.
例5:美美在拼图时,8个一样大小的长方形如图①那样,恰好可以拼成一个大的长方形.小红看见了,说:“我来试一试.”结果美美七拼八凑,拼成如图②那样的正方形.咳,怎么中间还留下了一个洞,恰好是边长为3
cm的小正方形!
请问:他们使用的小长方形的长
和宽分别是多少厘米?
解:
设小长方形的长、宽分别为x
cm,y
cm,
则
解得
答:他们使用的小长方形的长和宽分别是15
cm,9
cm.
3x=5y
2y-3=x
x=15
y=9
例6:小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
(1)用含x,y的式子表示地面总面积.
解:地面总面积为(6x+2y+18)m2.
例6:小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
(2)已知客厅面积比卫生间面积多21
m2,且地面总面积是卫生间面积的15倍.若铺1
m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
解:由题意得
解得
所以地面总面积为
所以铺地砖的总费用为
45×80=3
600(元).
例7:如图,在大长方形ABCD中,放入六个相同的小长方形,BC=11,DE=7,
(1)设每个小长方形的较长的一边为x,较短的一边为y,求x,y的值.
(2)求图中阴影部分面积.
解:设小长方形的长为x,宽为y,
根据题意得:
解得:
(2)S阴影=11×(8+1×1)-6×1×8=51
答:图中阴影部分面积是51.
例8:某校举办“迎亚运“学生书画展览,现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品.
(1)如图1,若大长方形的长和宽分别为45米和30米,求小长方形的长和宽.:
解:(1)设小长方形的长和宽分别为x米、y米
解得:
答:小长方形的长和宽分别为20米、5米;
例8:某校举办“迎亚运“学生书画展览,现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品.
(2)如图2,若大长方形的长和宽分别为a和b
①直接写出1个小长方形周长与大长方形周长之比;
②若作品展览区域(阴影部分)面积占展厅面
积的
①
1个小长方形周长与大长方形周长之比是1:3;
②
3、列二元一次方程组解行程与配套问题
1.基本关系式:
(1)相遇问题:同时不同地相向而行时,两人走的路程之和=两地距离.
(2)追及问题:同地不同时而行时,前者走的路程=追者走的路程;
同时不同地同向而行时,两人走的路程之差=两地距离.
(3)航行问题:顺流速度=静水速度+水流速度;
逆流速度=静水速度-水流速度.
例9:张明沿公路匀速前进,每隔4
min就遇到迎面开来的一辆公共汽车,每隔6
min就有一辆公共汽车从背后超过他.假定公共汽车的速度相同,且不变,而且迎面开来的相邻两车的距离和从背后开来的相邻两车的距离都是1
200
m.求张明前进的速度和公共汽车的速度.
解:
设张明前进的速度是x
m/min,公共汽车的速度是y
m/min.
根据题意,得
解这个方程组,得
答:张明前进的速度是50
m/min,公共汽车的速度是250
m/min.
4x+4y=1
200
6y-6x=1
200
x=50
y=250
例10:一列快车长100
m,慢车长300
m,若两车同向而行,快车从追上慢车到完全离开所用时间为10
s;若两车相向而行,两车从相遇到完全离开所用时间为2
s.求两车的平均速度.
解:设快车的平均速度为x
m/s,慢车的平均速度为y
m/s.
由题意,得
解得
答:快车的平均速度为120
m/s,慢车的平均速度为80
m/s.
10x-10y=300+100
2x+2y=300+100
x=120
y=80
例11:某教育服装厂要生产一批某种型号的学生服装,已知3
m长的布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,计划用600
m长的这种布料生产,应分别用多少布料生产上衣和裤子才能恰好配套?共能生产多少套?
解:设用x
m布料做上衣,ym布料做裤子
列方程组得
解得
答:用360
m布料生产上衣、240
m布料生产裤子才能恰好配套,共能生产240套.
例12:在某市“棚户区改造”建设工程中,有甲、乙两种车辆参加运土.已知5辆甲种车和2辆乙种车一次共可运土64
m3,3辆甲种车和1辆乙种车一次共可运土36
m3,求甲、乙两种车每辆一次分别可运土多少立方米.
解:设甲种车每辆一次可运土x
m3,
乙种车每辆一次可运土y
m3.
依题意得
解得
答:甲种车每辆一次可运土8
m3,乙种车每辆一次可运土12
m3.
5x+2y=64
3x+y=36
x=8
y=12
4、列二元一次方程组解百分率问题
1.关系式:
(1)增长率=
×100%;
(2)增长后的量=增长前的量×(1+增长率);
(3)亏损后的量=亏损前的量×(1-亏损率).
2.销售关系式:
(1)利润=总收入-总成本=单价×销量-总成本;
(2)利润率=
×100%;
(3)单价(售价)=进价+利润=(1+利润率)×进价.
另:打几折指按原单价的十分之几出售.
3.本息关系式:
(1)本息和=本金+利息;
(2)利息=本金×利率×期数.
例13:用二元一次方程组求解:某商场购进商品后,加价40%作为销售价,商场搞优惠促销,决定由顾客抽签确定折扣.某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款399元.两种商品原销售价之和为490元.则两种商品进价分别为多少元?
解:设甲种商品进价为a元,乙种商品进价为b元,
解得
答:甲乙两种商品进价分别为150元、200元.
例14:某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:
若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“国庆”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?
解:(1)设商场购进甲型号电视机x台,乙型号电视机y台,则
(2)迎“国庆”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?
解:(2)设甲种型号电视机打a折销售,
依题意得:15×(3640×0.75-2500)+35×(2025×0.1a-1500)=(15×2500+35×1500)×8.5%
解得a=8
答:甲种型号电视机打8折销售.
例15:小丽以两种方式分别储蓄了2
000元和1
000元,一年后全部取出,所得利息为64.8元,已知当时这两种储蓄方式年利率的和为4.23%.这两种储蓄方式的年利率各是百分之几(不计利息税)?
设存2
000元和1
000元的年利率分别是x%,y%.
由题意得:
解得
答:存2
000元和1
000元的年利率分别为2.25%,1.98%.
x+y=4.23
2000·x%+1000·y%=64.8
x=2.25
y=1.98
例16:甲、乙两个拖拉机厂,按计划每月共生产拖拉机460台,由于两厂都改进了技术,本月甲厂完成计划的110%,乙厂本月完成计划的115%,两厂共生产拖拉机519台,本月两厂各超额生产拖拉机多少台?
解:设甲厂计划生产拖拉机为x台,乙厂计划生产拖拉机为y台
由此可得方程组
解方程组得
故200×10%=20(台),260×115%=39(台),
答:甲、乙两厂超额生产的拖拉机分别为20台,39台.
5、列方程组解数字、工程、计数问题
1.数字关系式:
(1)一个三位数,百位数字为c,十位数字为b,个位数字为a,则该三位数可表示为_______________.
(2)用数位上的数字表示数的方法:个位上的数字×1,十位上的数字×10,百位上的数字×100,以此类推,然后把它们加起来就表示一个多位数.
100c+10b+a
2.
工程关系式:
(1)工作量=工作效率×工作时间
(2)总工作量=各部分工作量之和.
例17:一个两位自然数,其个位数字大于十位数字.现将其个位数字与十位数字调换位置,得到一个新数,且原数与新数的平均数为33.
(1)求原数的最小值;
(2)若原数的平方与新数的差为534,求原数与新数之积.
解:(1)设原两位数的个位数字为x,十位数字为y,(x>y),则原两位数是(10y+x),新两位数为(10x+y),根据题意得,
(10y+x)+(10x+y)=33×2,
∴x+y=6,
∵x、y均为正整数,x>y,
∴x=5,y=1或x=4,y=2,
∴原数的最小值15;
(2)若原数的平方与新数的差为534,求原数与新数之积.
(2)由(1)知,原数与新数可能为15与51,或24与42,
∵242-42=534,
∴24×42=1008.
例18.由甲、乙两运输队承包运输15000立方米沙石的任务,要求在10天之内(包含10天)完成.已知两队共有20辆汽车,甲队每辆车每天能够运输100立方米的沙石,乙队每辆车每天能够运输80立方米的沙石,前3天两队一共运输了5520立方米.
(1)求甲乙两队各有多少辆汽车?
(2)3天后,甲队另有紧急任务需要抽调车辆支援,在不影响工期的情况下,甲队最多可以抽调多少辆汽车走?
解:(1)设甲队有x辆汽车,乙队有y辆汽车,
根据题意得:
解得:
答:甲队有12辆汽车,乙队有8辆汽车,
(2)设甲队最多可以抽调m辆汽车走,
根据题意得:
7[100(12-m)+80×8]≥15000-5520,
解得:
m最大的整数是4,
答:甲队最多可以抽调4辆汽车走.
例19:若干名工人装卸一批货物,每名工人装卸速度相同,如果这些工人同时工作,则需10小时完成,现在改变装卸方式,开始一个人干,以后每隔t小时(t为整数)增加一个人,每个参加装卸的人都一直干到装卸结束,且最后增加的一个人装卸的时间是第一个人装卸时间的四分之一.问:
(1)改变后的装卸方式,自始至终需要多长时间?
(2)参加装卸的工人有多少名?
(1)解:设装卸工作需x小时完成
解得:x=16.
答:改变后的装卸方式,自始至终需要16小时.
(2)设共有y人参加装卸工作,由于每隔t小时增加一人,因此最后一人比第一人少(y-1)t小时
依题意,得:
∴(y-1)t=12.
∵y,t均为正整数,
1、y=2,t=12
2、y=3,t=6
3、y=4,t=4
4、y=5,t=3
5、y=7,t=2
参加装卸的工人有2或3或4或5或7或13名.
巩固与提高
某公司有如图所示的甲、乙、丙、丁四个生产基地.现决定在其中一个基地修建总仓库,以方便公司对各基地生产的产品进行集中存储.已知甲、乙、丙、丁各基地的产量之比等于4:5:4:2,各基地之间的距离之比a:b:c:d:e=2:3:4:3:3(因条件限制,只有图示中的五条运输渠道),当产品的运输数量和运输路程均相等时,所需的运费相等.若要使总运费最低,则修建总仓库的最佳位置为( )
甲
完成课后作业
数学七年级下册第八章二元一次方程组
8.3
实际问题与二元一次方程组
学习目标
1、列二元一次方程组解和、差、倍、分问题
2、列二元一次方程组解几何问题
3、列二元一次方程组解行程与配套问题
4、列二元一次方程组解百分率问题
5、列方程组解数字、工程、计数问题
一、列二元一次方程组解和、差、倍、分问题
步骤
审题:弄清题意和题目中的
设元:用_____表示题目中的未知数
解方程组
检验作答
数量关系
字母
2
代入法;
加减法.
列方程组:根据_2_个等量关系列出方程组
例1:小明买了50分和20分的邮票共16枚,花了5元9角钱,20分和50分的邮票各买了多少枚?根据题意完成下列各题:
(1)设小明买了20分的邮票x枚,则50分的邮票买了_____________枚,由题意可得一元一次方程______________________.
(16-x)
20x+(16-x)×50=590
(2)设20分的邮票买了x枚,50分的邮票买了y枚,由题意可得二元一次方程组
(3)设买20分的邮票花了x元,买50分的邮票花了y元,由题意可得二元一次方程组
x+y=16
20x+50y=590
例2:列方程解应用题:《九章算术》中有“盈不足术”的问题,原文如下:“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”
题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元,求人数和羊价各是多少.
解:设买羊人共有x人,羊价为y元.
由题意得
,
解得
答:买羊人共有21人,羊价为150元.
y=5x+45
y=7x+3
x=21
y=150
解:
设每名熟练工人和新工人每月分别可以安装x、y辆电动汽车,根据题意,得
解之得
x+2y=8
2x+3y=14.
答:每名熟练工和新工人每月分别可以安装4辆、2辆电动汽车.
例3.某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.则每名熟练工和新工人每月分别可以安装多少辆电动汽车?
x=4
y=2.
例4:《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱.如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的
,那么乙也共有钱48文
.甲、乙两人原来各有多少钱?
解:设甲原有x文钱,乙原有y文钱,
由题意可得
解得:
答:甲原有36文钱,乙原有24文钱.
2、列二元一次方程组解几何问题
用二元一次方程组解几何图形问题时,要根据几何图形的性质、公式结合图形中反映的数量关系,建立二元一次方程组的模型.
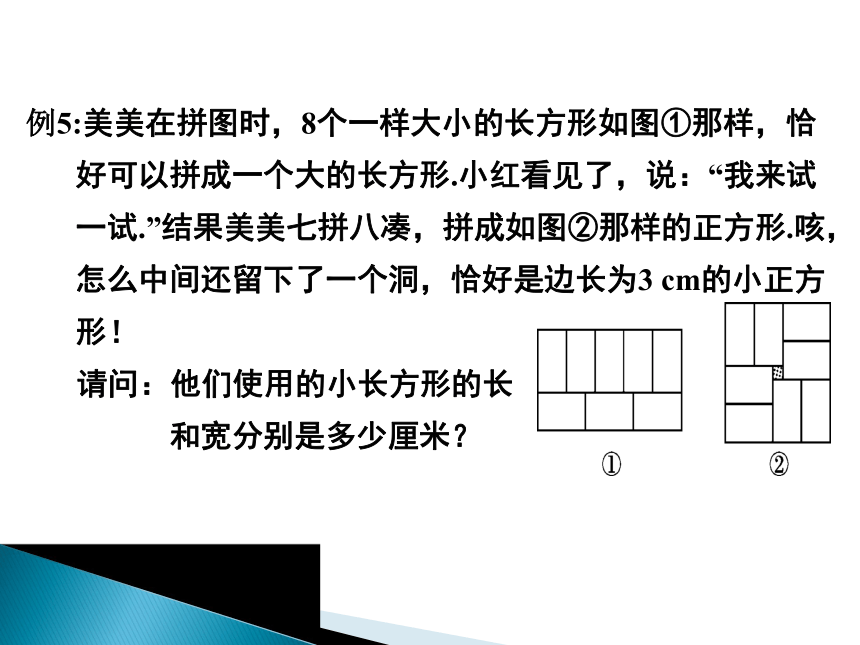
例5:美美在拼图时,8个一样大小的长方形如图①那样,恰好可以拼成一个大的长方形.小红看见了,说:“我来试一试.”结果美美七拼八凑,拼成如图②那样的正方形.咳,怎么中间还留下了一个洞,恰好是边长为3
cm的小正方形!
请问:他们使用的小长方形的长
和宽分别是多少厘米?
解:
设小长方形的长、宽分别为x
cm,y
cm,
则
解得
答:他们使用的小长方形的长和宽分别是15
cm,9
cm.
3x=5y
2y-3=x
x=15
y=9
例6:小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
(1)用含x,y的式子表示地面总面积.
解:地面总面积为(6x+2y+18)m2.
例6:小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
(2)已知客厅面积比卫生间面积多21
m2,且地面总面积是卫生间面积的15倍.若铺1
m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
解:由题意得
解得
所以地面总面积为
所以铺地砖的总费用为
45×80=3
600(元).
例7:如图,在大长方形ABCD中,放入六个相同的小长方形,BC=11,DE=7,
(1)设每个小长方形的较长的一边为x,较短的一边为y,求x,y的值.
(2)求图中阴影部分面积.
解:设小长方形的长为x,宽为y,
根据题意得:
解得:
(2)S阴影=11×(8+1×1)-6×1×8=51
答:图中阴影部分面积是51.
例8:某校举办“迎亚运“学生书画展览,现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品.
(1)如图1,若大长方形的长和宽分别为45米和30米,求小长方形的长和宽.:
解:(1)设小长方形的长和宽分别为x米、y米
解得:
答:小长方形的长和宽分别为20米、5米;
例8:某校举办“迎亚运“学生书画展览,现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品.
(2)如图2,若大长方形的长和宽分别为a和b
①直接写出1个小长方形周长与大长方形周长之比;
②若作品展览区域(阴影部分)面积占展厅面
积的
①
1个小长方形周长与大长方形周长之比是1:3;
②
3、列二元一次方程组解行程与配套问题
1.基本关系式:
(1)相遇问题:同时不同地相向而行时,两人走的路程之和=两地距离.
(2)追及问题:同地不同时而行时,前者走的路程=追者走的路程;
同时不同地同向而行时,两人走的路程之差=两地距离.
(3)航行问题:顺流速度=静水速度+水流速度;
逆流速度=静水速度-水流速度.
例9:张明沿公路匀速前进,每隔4
min就遇到迎面开来的一辆公共汽车,每隔6
min就有一辆公共汽车从背后超过他.假定公共汽车的速度相同,且不变,而且迎面开来的相邻两车的距离和从背后开来的相邻两车的距离都是1
200
m.求张明前进的速度和公共汽车的速度.
解:
设张明前进的速度是x
m/min,公共汽车的速度是y
m/min.
根据题意,得
解这个方程组,得
答:张明前进的速度是50
m/min,公共汽车的速度是250
m/min.
4x+4y=1
200
6y-6x=1
200
x=50
y=250
例10:一列快车长100
m,慢车长300
m,若两车同向而行,快车从追上慢车到完全离开所用时间为10
s;若两车相向而行,两车从相遇到完全离开所用时间为2
s.求两车的平均速度.
解:设快车的平均速度为x
m/s,慢车的平均速度为y
m/s.
由题意,得
解得
答:快车的平均速度为120
m/s,慢车的平均速度为80
m/s.
10x-10y=300+100
2x+2y=300+100
x=120
y=80
例11:某教育服装厂要生产一批某种型号的学生服装,已知3
m长的布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,计划用600
m长的这种布料生产,应分别用多少布料生产上衣和裤子才能恰好配套?共能生产多少套?
解:设用x
m布料做上衣,ym布料做裤子
列方程组得
解得
答:用360
m布料生产上衣、240
m布料生产裤子才能恰好配套,共能生产240套.
例12:在某市“棚户区改造”建设工程中,有甲、乙两种车辆参加运土.已知5辆甲种车和2辆乙种车一次共可运土64
m3,3辆甲种车和1辆乙种车一次共可运土36
m3,求甲、乙两种车每辆一次分别可运土多少立方米.
解:设甲种车每辆一次可运土x
m3,
乙种车每辆一次可运土y
m3.
依题意得
解得
答:甲种车每辆一次可运土8
m3,乙种车每辆一次可运土12
m3.
5x+2y=64
3x+y=36
x=8
y=12
4、列二元一次方程组解百分率问题
1.关系式:
(1)增长率=
×100%;
(2)增长后的量=增长前的量×(1+增长率);
(3)亏损后的量=亏损前的量×(1-亏损率).
2.销售关系式:
(1)利润=总收入-总成本=单价×销量-总成本;
(2)利润率=
×100%;
(3)单价(售价)=进价+利润=(1+利润率)×进价.
另:打几折指按原单价的十分之几出售.
3.本息关系式:
(1)本息和=本金+利息;
(2)利息=本金×利率×期数.
例13:用二元一次方程组求解:某商场购进商品后,加价40%作为销售价,商场搞优惠促销,决定由顾客抽签确定折扣.某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款399元.两种商品原销售价之和为490元.则两种商品进价分别为多少元?
解:设甲种商品进价为a元,乙种商品进价为b元,
解得
答:甲乙两种商品进价分别为150元、200元.
例14:某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:
若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“国庆”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?
解:(1)设商场购进甲型号电视机x台,乙型号电视机y台,则
(2)迎“国庆”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?
解:(2)设甲种型号电视机打a折销售,
依题意得:15×(3640×0.75-2500)+35×(2025×0.1a-1500)=(15×2500+35×1500)×8.5%
解得a=8
答:甲种型号电视机打8折销售.
例15:小丽以两种方式分别储蓄了2
000元和1
000元,一年后全部取出,所得利息为64.8元,已知当时这两种储蓄方式年利率的和为4.23%.这两种储蓄方式的年利率各是百分之几(不计利息税)?
设存2
000元和1
000元的年利率分别是x%,y%.
由题意得:
解得
答:存2
000元和1
000元的年利率分别为2.25%,1.98%.
x+y=4.23
2000·x%+1000·y%=64.8
x=2.25
y=1.98
例16:甲、乙两个拖拉机厂,按计划每月共生产拖拉机460台,由于两厂都改进了技术,本月甲厂完成计划的110%,乙厂本月完成计划的115%,两厂共生产拖拉机519台,本月两厂各超额生产拖拉机多少台?
解:设甲厂计划生产拖拉机为x台,乙厂计划生产拖拉机为y台
由此可得方程组
解方程组得
故200×10%=20(台),260×115%=39(台),
答:甲、乙两厂超额生产的拖拉机分别为20台,39台.
5、列方程组解数字、工程、计数问题
1.数字关系式:
(1)一个三位数,百位数字为c,十位数字为b,个位数字为a,则该三位数可表示为_______________.
(2)用数位上的数字表示数的方法:个位上的数字×1,十位上的数字×10,百位上的数字×100,以此类推,然后把它们加起来就表示一个多位数.
100c+10b+a
2.
工程关系式:
(1)工作量=工作效率×工作时间
(2)总工作量=各部分工作量之和.
例17:一个两位自然数,其个位数字大于十位数字.现将其个位数字与十位数字调换位置,得到一个新数,且原数与新数的平均数为33.
(1)求原数的最小值;
(2)若原数的平方与新数的差为534,求原数与新数之积.
解:(1)设原两位数的个位数字为x,十位数字为y,(x>y),则原两位数是(10y+x),新两位数为(10x+y),根据题意得,
(10y+x)+(10x+y)=33×2,
∴x+y=6,
∵x、y均为正整数,x>y,
∴x=5,y=1或x=4,y=2,
∴原数的最小值15;
(2)若原数的平方与新数的差为534,求原数与新数之积.
(2)由(1)知,原数与新数可能为15与51,或24与42,
∵242-42=534,
∴24×42=1008.
例18.由甲、乙两运输队承包运输15000立方米沙石的任务,要求在10天之内(包含10天)完成.已知两队共有20辆汽车,甲队每辆车每天能够运输100立方米的沙石,乙队每辆车每天能够运输80立方米的沙石,前3天两队一共运输了5520立方米.
(1)求甲乙两队各有多少辆汽车?
(2)3天后,甲队另有紧急任务需要抽调车辆支援,在不影响工期的情况下,甲队最多可以抽调多少辆汽车走?
解:(1)设甲队有x辆汽车,乙队有y辆汽车,
根据题意得:
解得:
答:甲队有12辆汽车,乙队有8辆汽车,
(2)设甲队最多可以抽调m辆汽车走,
根据题意得:
7[100(12-m)+80×8]≥15000-5520,
解得:
m最大的整数是4,
答:甲队最多可以抽调4辆汽车走.
例19:若干名工人装卸一批货物,每名工人装卸速度相同,如果这些工人同时工作,则需10小时完成,现在改变装卸方式,开始一个人干,以后每隔t小时(t为整数)增加一个人,每个参加装卸的人都一直干到装卸结束,且最后增加的一个人装卸的时间是第一个人装卸时间的四分之一.问:
(1)改变后的装卸方式,自始至终需要多长时间?
(2)参加装卸的工人有多少名?
(1)解:设装卸工作需x小时完成
解得:x=16.
答:改变后的装卸方式,自始至终需要16小时.
(2)设共有y人参加装卸工作,由于每隔t小时增加一人,因此最后一人比第一人少(y-1)t小时
依题意,得:
∴(y-1)t=12.
∵y,t均为正整数,
1、y=2,t=12
2、y=3,t=6
3、y=4,t=4
4、y=5,t=3
5、y=7,t=2
参加装卸的工人有2或3或4或5或7或13名.
巩固与提高
某公司有如图所示的甲、乙、丙、丁四个生产基地.现决定在其中一个基地修建总仓库,以方便公司对各基地生产的产品进行集中存储.已知甲、乙、丙、丁各基地的产量之比等于4:5:4:2,各基地之间的距离之比a:b:c:d:e=2:3:4:3:3(因条件限制,只有图示中的五条运输渠道),当产品的运输数量和运输路程均相等时,所需的运费相等.若要使总运费最低,则修建总仓库的最佳位置为( )
甲
完成课后作业
