北师大版八年级下册数学课件:6.1平行四边形性质(一)(共17张PPT)
文档属性
| 名称 | 北师大版八年级下册数学课件:6.1平行四边形性质(一)(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 738.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-05 09:03:15 | ||
图片预览





文档简介
(共17张PPT)
学习目标:
1.理解平行四边形的定义及相关概念.
2.掌握并能运用平行四边形对边相等、对角相等的性质.
自主学习
自学教材P135完成学习卡上问题一的第1—4题
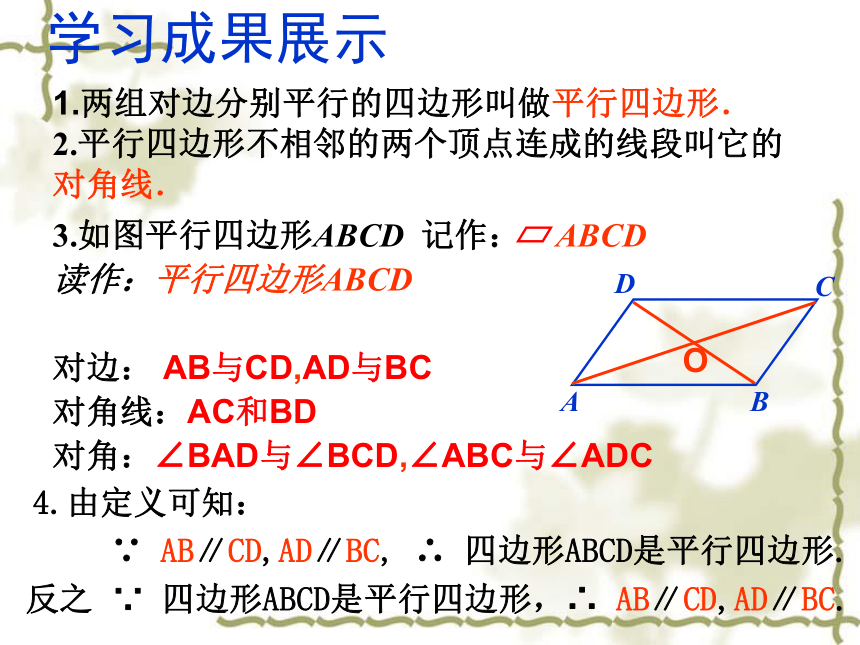
1.两组对边分别平行的四边形叫做平行四边形.
3.如图平行四边形ABCD
记作:
ABCD
读作:平行四边形ABCD
对边:
AB与CD,AD与BC
对角线:AC和BD
对角:∠BAD与∠BCD,∠ABC与∠ADC
2.平行四边形不相邻的两个顶点连成的线段叫它的对角线.
4.由定义可知:
∵
AB∥CD,AD∥BC,
∴
四边形ABCD是平行四边形.
反之
∵
四边形ABCD是平行四边形,∴
AB∥CD,AD∥BC.
学习成果展示
用一张平行四边形纸片绕它的对角线交点顺时针(或逆时针)旋转180°观察图形变化,探索平行四边形的性质.
(1)平行四边形是中心对称图形吗?
(2)你还发现平行四边形的对边、对角有什么数量关系?
合作探究
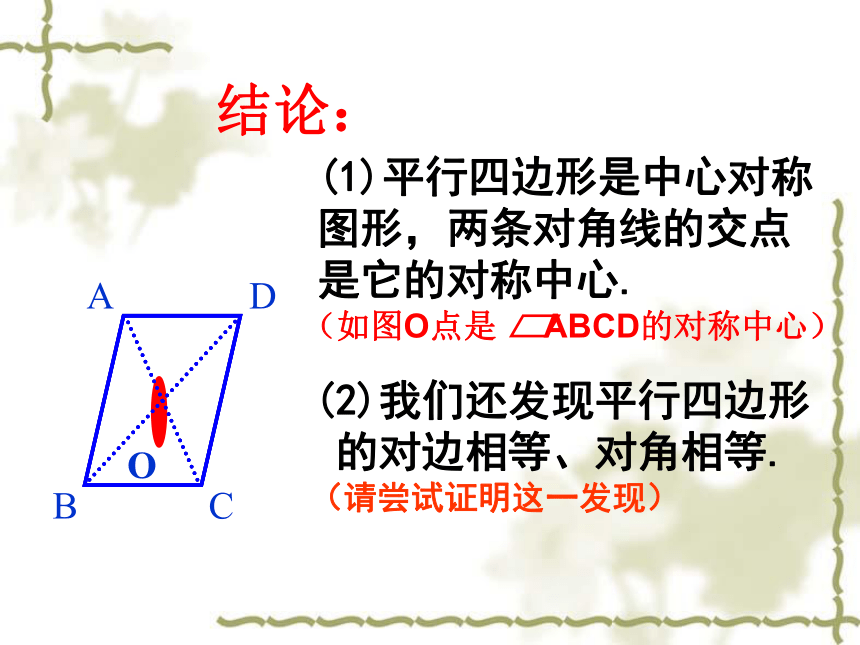
结论:
(1)平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
(如图O点是
ABCD的对称中心)
(2)我们还发现平行四边形的对边相等、对角相等.
(请尝试证明这一发现)
已知:如图,四边形
ABCD是平行四边形
求证:AB=CD,BC=DA;∠B=∠D,∠A=∠C.
即∠BAD=∠DCB.
证明:连结AC
∴AB∥CD,AD∥BC(平行四边形的定义)
∴∠1=∠2,∠3=∠4
∵AC=CA,
∴△ABC≌△CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3,
A
B
C
D
∵四边形
ABCD是平行四边形
1.完成学习卡上问题三第1—5题.
2.时间6分钟左右.
3.提前完成的同学帮助有困难的同学.
巩固练习
成果汇报
自己回答
在
ABCD
中,
已知一个内角的度数是∠A=60°,则其余三个内角的度数分别为:
.
∠C=60°,∠B=120°,
∠D=120°
如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为10m,其他三条边分别为
:
.
CD=10m、
BC=8m、AD=8m
同桌回答
已知:在
ABCD中,E、F是对角线AC上的两点,并且AE=CF.
求证:BE=DF
A
F
E
D
C
B
师生共同完成
证明:
∵
四边形ABCD是平行四边形,
∴
AB=CD(平行四边形对边相等),
AB∥CD(平行四边形定义).
∴
∠BAE=∠DCF.
又∵
AE=CF,
∴
△ABE=△CDF(SAS).
∴
BE=DF.
A
B
C
D
已知:
ABCD的周长等于20
cm,
AC=7
cm,△ABC的周长为:
.
17cm
请同学回答
在□ABCD中,∠A∶∠B∶∠C∶∠D的值可以是(
)
A.1∶2∶3∶4
B.1∶2∶2∶1
C.1∶1∶2∶2
D.2∶1∶2∶1
D
全班齐答
如图所示有一块平行四边形形状的玻璃,不小心把EDF部分打碎了现在只测得:AE=60cm,AB=70cm,BC=80cm,CF=15cm,∠B=60°.你能根据测得的数据计算DE、DF的长度和∠D的度数吗?
问题解决
解:∵
四边形ABCD是平行四边形,
∴
CD=AB=70cm,AD=BC=80cm,
∠D=∠B=60°.
∴
DE=AD-AE=80-60=20cm,
DF=CD-CF=70-15=55cm.
谈谈你这节课有什么收获?
回顾总结
课后作业
P137习题6.1.
必做:第1、2、3题
选做:第4题
学习目标:
1.理解平行四边形的定义及相关概念.
2.掌握并能运用平行四边形对边相等、对角相等的性质.
自主学习
自学教材P135完成学习卡上问题一的第1—4题
1.两组对边分别平行的四边形叫做平行四边形.
3.如图平行四边形ABCD
记作:
ABCD
读作:平行四边形ABCD
对边:
AB与CD,AD与BC
对角线:AC和BD
对角:∠BAD与∠BCD,∠ABC与∠ADC
2.平行四边形不相邻的两个顶点连成的线段叫它的对角线.
4.由定义可知:
∵
AB∥CD,AD∥BC,
∴
四边形ABCD是平行四边形.
反之
∵
四边形ABCD是平行四边形,∴
AB∥CD,AD∥BC.
学习成果展示
用一张平行四边形纸片绕它的对角线交点顺时针(或逆时针)旋转180°观察图形变化,探索平行四边形的性质.
(1)平行四边形是中心对称图形吗?
(2)你还发现平行四边形的对边、对角有什么数量关系?
合作探究
结论:
(1)平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
(如图O点是
ABCD的对称中心)
(2)我们还发现平行四边形的对边相等、对角相等.
(请尝试证明这一发现)
已知:如图,四边形
ABCD是平行四边形
求证:AB=CD,BC=DA;∠B=∠D,∠A=∠C.
即∠BAD=∠DCB.
证明:连结AC
∴AB∥CD,AD∥BC(平行四边形的定义)
∴∠1=∠2,∠3=∠4
∵AC=CA,
∴△ABC≌△CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3,
A
B
C
D
∵四边形
ABCD是平行四边形
1.完成学习卡上问题三第1—5题.
2.时间6分钟左右.
3.提前完成的同学帮助有困难的同学.
巩固练习
成果汇报
自己回答
在
ABCD
中,
已知一个内角的度数是∠A=60°,则其余三个内角的度数分别为:
.
∠C=60°,∠B=120°,
∠D=120°
如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为10m,其他三条边分别为
:
.
CD=10m、
BC=8m、AD=8m
同桌回答
已知:在
ABCD中,E、F是对角线AC上的两点,并且AE=CF.
求证:BE=DF
A
F
E
D
C
B
师生共同完成
证明:
∵
四边形ABCD是平行四边形,
∴
AB=CD(平行四边形对边相等),
AB∥CD(平行四边形定义).
∴
∠BAE=∠DCF.
又∵
AE=CF,
∴
△ABE=△CDF(SAS).
∴
BE=DF.
A
B
C
D
已知:
ABCD的周长等于20
cm,
AC=7
cm,△ABC的周长为:
.
17cm
请同学回答
在□ABCD中,∠A∶∠B∶∠C∶∠D的值可以是(
)
A.1∶2∶3∶4
B.1∶2∶2∶1
C.1∶1∶2∶2
D.2∶1∶2∶1
D
全班齐答
如图所示有一块平行四边形形状的玻璃,不小心把EDF部分打碎了现在只测得:AE=60cm,AB=70cm,BC=80cm,CF=15cm,∠B=60°.你能根据测得的数据计算DE、DF的长度和∠D的度数吗?
问题解决
解:∵
四边形ABCD是平行四边形,
∴
CD=AB=70cm,AD=BC=80cm,
∠D=∠B=60°.
∴
DE=AD-AE=80-60=20cm,
DF=CD-CF=70-15=55cm.
谈谈你这节课有什么收获?
回顾总结
课后作业
P137习题6.1.
必做:第1、2、3题
选做:第4题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
