第一轮复习圆的有关性质

(共17张PPT)
第四章 图形的认识
第十六节：圆的概念和性质
知识网络知识点、考点聚焦
典型例题解析
课时训练
知识网络
(一)圆的概念
1．圆的定义：圆是到定点的距离等于定长的点的
集合．
2．定理：，不在同一直线上的三个点确定一个圆．
3．作三角形外接圆的方法：先作三角形两边的中
垂线得到三角形外心，再以外心为圆心，外心到三
角形一个顶点的距离为半径作圆．
(二)圆的性质
1．圆为轴对称图形，经过圆心的每一条直线都是
它的对称轴．
垂径定理：垂直于弦的直径平分这条弦，
并且平分弦所对的两条弧．
推论(1)平分弦(不是直径)的直径垂直于弦，并且
平分弦所对的两条弧．
(2)弦的垂直平分线经过圆心，并且平分弦所对的
两条弧．
(3)平分弦所对的一条弧的直径，垂直平分弦，
并且平分弦所对的另一条弧．
(4)圆的两条平行弦所夹的弧相等．
2．圆是以圆心为对称中心的中心对称图形．
定理：在同圆或等圆中，相等的圆心角所对的弧
相等，所对的弦相等，所对的弦的弦心距相等．
推论：在同圆或等圆中，如果两个圆心角、两条弧、
两条弦或两条弦的弦心距中有一组相等时，那么
它们所对的其余各组量都分别相等．
3．圆周角
(1)定义：顶点在圆上并且两边都和圆相交的角．
(2)定理：一条弧所对的圆周角等于它所对的圆心角
的一半．
推论：①同弧或等弧所对的圆周角相等；同圆或等
圆中，相等的圆周角所对的弧也相等．
②半圆(或直径)所对的圆周角为直角；90°的圆周
角所对的弦为直径．
③如果三角形一边上的中线等于这边的一半，那么
这个三角形为直角三角形．
4．圆内接四边形的性质定理：圆的内接四边形的
对角互补，并且任何一个外角都等于它的内对角．
典例精析
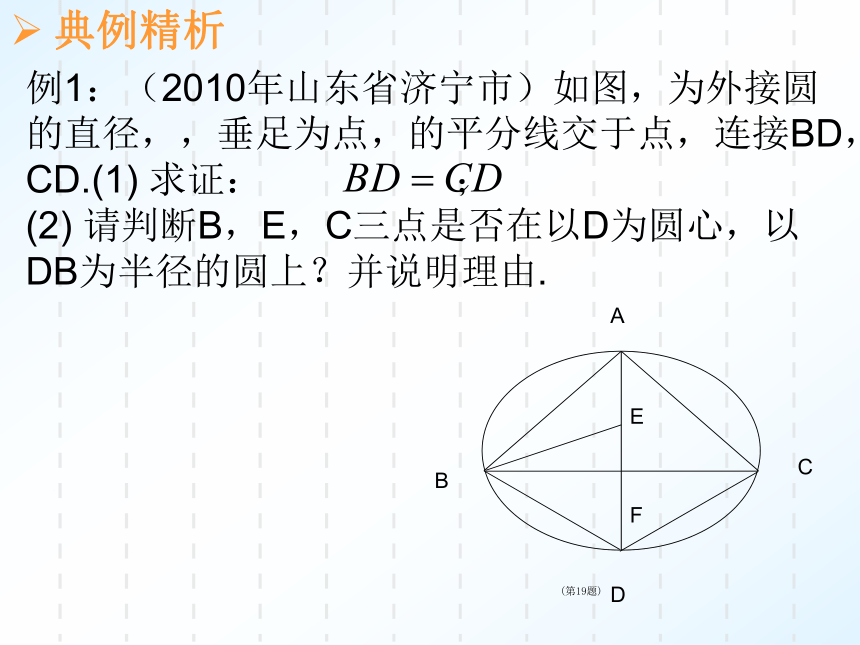
例1：（2010年山东省济宁市）如图，为外接圆的直径，，垂足为点，的平分线交于点，连接BD，CD.(1) 求证： ；
(2) 请判断B，E，C三点是否在以D为圆心，以DB为半径的圆上？并说明理由.
(第19题)
A
B
D
E
F
C
例2：（2010年宁德市）如图，在直径AB＝12的⊙O中，弦CD⊥AB于M，且M是半径OB的中点，则弦CD的长是_______（结果保留根号）.
M
·
A
B
C
D
OO
M
第17题图
A
B
C
D
例3、（2010江苏宿迁）如图，在平面直角坐标系
中，O为原点，每个小方格的边长为1个单位长度．
在第一象限内有横、纵坐标均为整数的A、B两点，
且OA= OB=
．
（1）写出A、B两点的坐标；
（2）画出线段AB绕点O旋转一周所形成的图形，
并求其面积（结果保留π）．
例4、（2010日照市）24．(本题满分10分)如图，
在△ABC中，AB=AC，以AB为直径的⊙O交AC
与E，交BC与D．求证：
（1）D是BC的中点；
（2）△BEC∽△ADC；
（3）BC2=2AB·CE．
课时训练
1、(2010年安徽省芜湖市)如图所示，在圆⊙O内
有折线OABC，其中OA＝8，AB＝12，∠A＝∠B
＝60°，则BC的长为（）
A．19 B．16 C．18 D．20
2、（2010年浙江台州市）如图，⊙O的直径
CD⊥AB，∠AOC=50°，则∠CDB大小为 ( )
A．25° B．30° C．40° D．50°
（第5题）
A
B
O
C
D
3、（2010江西）如图，以点P为圆心的圆弧与X
轴交于A，B；两点，点P的坐标为（4，2）点A
的坐标为（2，0）则点B的坐标为 ．
4、（2010年宁德市）如图，在⊙O中，
∠ACB＝34°，则∠AOB的度数是（ ）．
A.17° B.34° C.56° D.68°
第5题图
A
O
C
B
5、（2010江苏泰州，18，3分）如图⊙O的半径为
1cm，弦AB、CD的长度分别为
，则弦AC、BD所夹的锐角
＝ ．
6、(2010·珠海中考)如图，△ABC内接于⊙O，AB＝6,AC＝4,D是AB边上一点，P是优弧BAC的中点，连结PA、PB、PC、PD.
(1)当BD的长度为多少时，△PAD是以AD为底边的等腰三角形？并证明；
(2)若cos∠PCB= ，求PA的长.