人教版八年级数学下册第二十章 数据的分析单元检测卷(含答案)
文档属性
| 名称 | 人教版八年级数学下册第二十章 数据的分析单元检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 387.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-04 15:30:45 | ||
图片预览



文档简介
人教版八年级数学下册第二十章
数据的分析
单元检测卷
一、选择题
1.自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是(
)
A.3
B.4
C.5
D.6
2.已知一组数据x1,x2,x3的平均数为6,则数据x1+1,x2+1,x3+1的平均数为(
)
A.6 B.7 C.9 D.12
3.要判断某同学的数学考试成绩是否稳定,那么需要知道他最近几次数学考试成绩的(
)
A.方差
B.众数
C.平均数
D.中位数
4.某居民小区开展节约用电活动,对该小区100户家庭的节电量情况进行了统计,4月份与3月份相比,节电情况如下表,则4月份这100户节电量的平均数、中位数、众数分别是(
)
节电量(千瓦时)
20
30
40
50
户数
10
40
30
20
A.35、35、30
B.25、30、20
C.36、35、30
D.36、30、30
5.下表是利群超市5月份一周的利润情况记录:
日期
12日
13日
14日
15日
16日
17日
18日
当日利
润(万元)
0.20
0.17
0.23
0.21
0.23
0.18
0.25
根据上表,你估计利群超市该年5月份的总利润是(
)
(A)6.51万元
(B)6.4万元
(C)1.47万元
(D)5.88万元
6.小明记录了一星期每天的最高气温如下表,则这个星期每天的最高气温的中位数是(
)
星期
一
二
三
四
五
六
日
最高气温(℃)
22
24
23
25
24
22
21
A.22
℃
B.23
℃
C.24
℃
D.25
℃
7.若数据x1,x2,…,xn的众数为a,方差为b,则数据x1+2,x2+2,…,xn+2的众数、方差分别是(
)
(A)a,b
(B)a,b+2
(C)a+2,b
(D)a+2,b+2
8.若有①分析数据;②收集数据;③作出决策;④整理数据;⑤提出问题,则下列关于决策过程的排序正确的是(
)
A.⑤②④①③
B.⑤②①③④
C.④①③②⑤
D.⑤③②④①
9.若样本x1+1,x2+1,x3+1,……,xn+1的平均数为18,方差为2,则对于样本x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是(
)
A.平均数为18,方差为2
B.平均数为19,方差为3
C.平均数为19,方差为2
D.平均数为20,方差为4
10.一次统计八(2)班若干名学生每分钟跳绳次数的频数分布直方图如图所示.由这个直方图可知,这若干名学生平均每分钟跳绳的次数(结果精确到个位)是(
)
(A)数据不全无法计算
(B)103
(C)104
(D)105
填空题
11.在数据-1、0、4、5、8中插入一个数据x,使得该组数据的中位数是3,则x=_________.
12.在一次爱心捐款中,某班有40名学生拿出自己的零花钱,有捐5元、10元、20元、50元的,如图反映了不同捐款的人数比例,那么这个班的学生平均每人捐款
元.
甲、乙两台机床生产同一种零件,并且每天产量相等,在6天中每天生产零件中的次品数依次是:甲:3,0,0,2,0,1;乙:1,0,2,1,0,2.则甲、乙两台机床中性能较稳定的是 .
14.小明用s2=[(x1-3)2+(x2-3)2+…+(x10-3)2]计算一组数据的方差,那么x1+x2+x3+…+x10= .?
15.某公司销售部有营销人员25人,销售部为了制订某种商品的销售定额,统计了这25人某月的销售量如下表:
每人销售量(单位:件)
600
500
400
350
300
200
人数(单位:人)
1
4
4
6
7
3
公司营销人员该月销售量的中位数是 .?
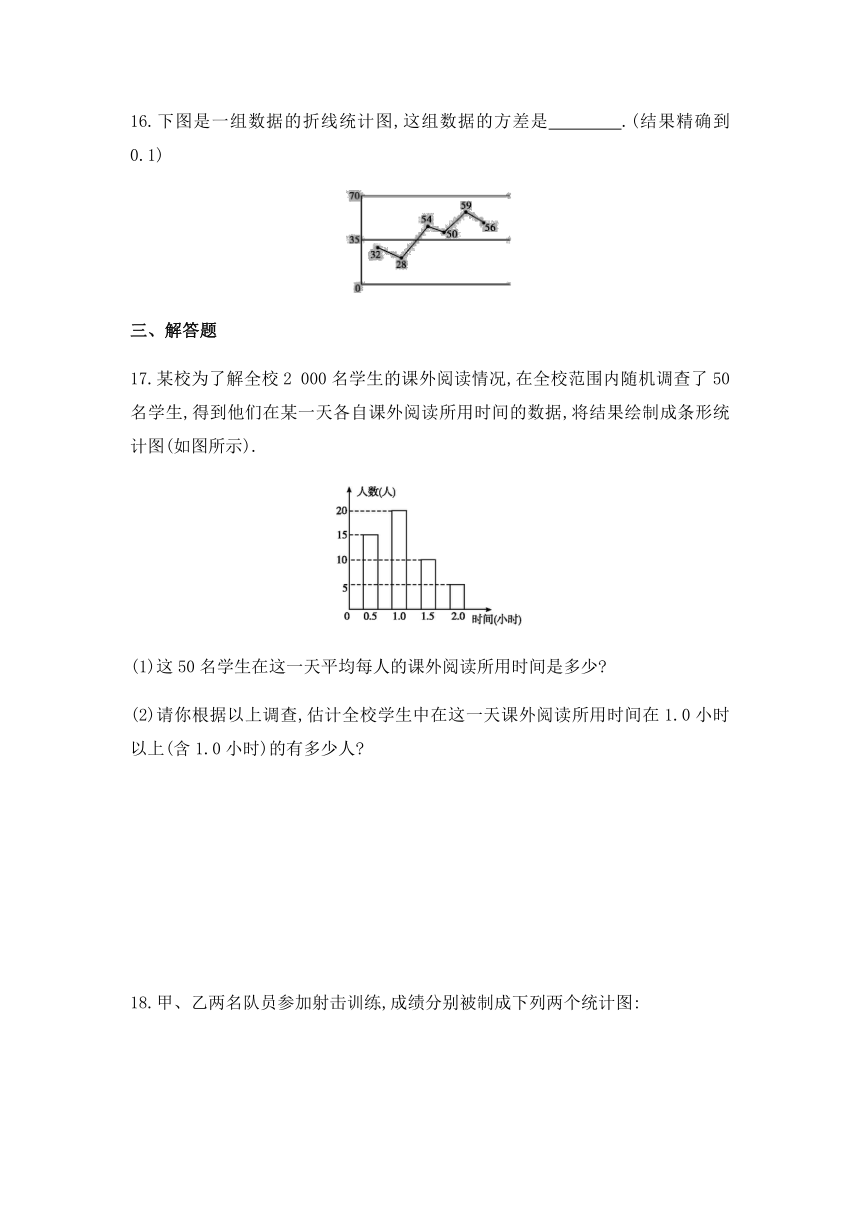
16.下图是一组数据的折线统计图,这组数据的方差是 .(结果精确到0.1)?
三、解答题
17.某校为了解全校2
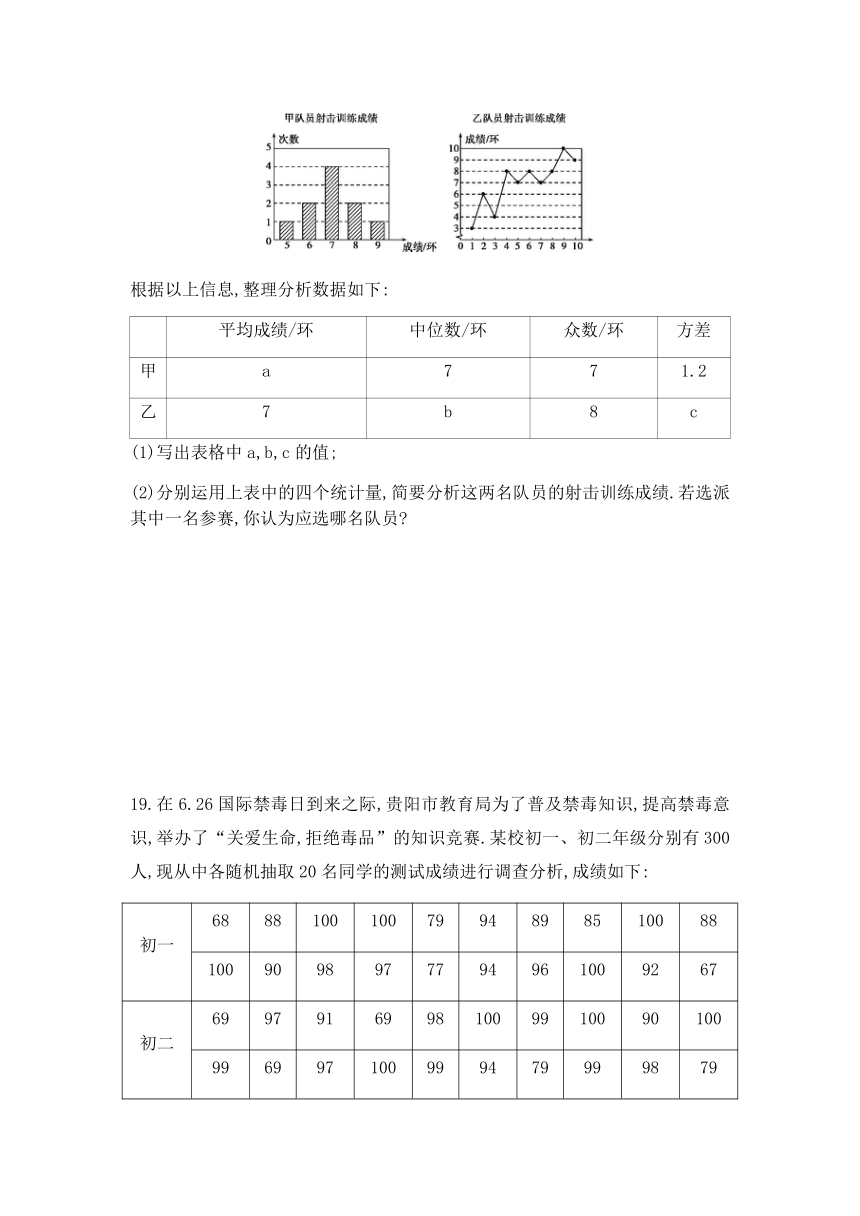
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
18.甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用上表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
19.在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二
69
97
91
69
98
100
99
100
90
100
99
69
97
100
99
94
79
99
98
79
(1)根据上述数据,将下列表格补充完整.
整理、描述数据:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
2
4
12
初二人数
2
2
1
15
分析数据:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
91.3
?
20%
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 (人);?
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
20.爸爸为了解小明这学期在家的作息时间,随机挑选了某个星期对小明进行了观察,并记录了他娱乐的时间(单位:min):
日期
周一
周二
周三
周四
周五
周六
周日
娱乐时间
55
60
70
65
50
240
370
(1)分别计算小明这周内娱乐时间的平均数和中位数;
(2)应选中位数和平均数中的哪一个表示小明这一周的一般娱乐时间更好?为什么?
(3)能否用(2)的数据表示本学期小明在家娱乐的一般时间?为什么?
21.某厂生产A,B两种产品,其单价随市场变化而进行相应的调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
并求得了A产品三次单价的平均数和方差:=5.9,=×[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=.
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;?
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
22.某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如下.
(1)求出下列成绩统计分析表中a,b的值;
组别
平均分
中位数
方差
合格率
优秀率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
23.一家商场张贴了下列海报:
好消息
在庆祝本店开业20周年之际,特举办“真情回报新老顾客”活动.本次活动共设奖金20万元,平均每份奖金200元,特等奖1万元!凡在本店购买物品金额满100元者均可参加抽奖.
一些顾客参加了抽奖,但没有一人的奖金超过50元,于是他们一起质问商场经理.商场经理拿出了下面一张表格:
奖金等级
特等奖
一等奖
二等奖
三等奖
四等奖
奖金额/元
10
000
6
000
1
000
50
10
中奖人数
3
10
87
350
550
你认为海报上写的“平均每份奖金200元”是否欺骗了顾客?用数据的哪种特征数最能代表获奖金额?说说你的理由.
24.某市某中学举行“中国梦·校园好声音”歌手大赛,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩统计情况如图所示.
(1)根据统计图填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,判断哪一个代表队选手的成绩较为稳定.
参考答案
一、选择题
1.自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是( B )
A.3
B.4
C.5
D.6
2.已知一组数据x1,x2,x3的平均数为6,则数据x1+1,x2+1,x3+1的平均数为( B )
A.6 B.7 C.9 D.12
3.要判断某同学的数学考试成绩是否稳定,那么需要知道他最近几次数学考试成绩的( A )
A.方差
B.众数
C.平均数
D.中位数
4.某居民小区开展节约用电活动,对该小区100户家庭的节电量情况进行了统计,4月份与3月份相比,节电情况如下表,则4月份这100户节电量的平均数、中位数、众数分别是( C )
节电量(千瓦时)
20
30
40
50
户数
10
40
30
20
A.35、35、30
B.25、30、20
C.36、35、30
D.36、30、30
5.下表是利群超市5月份一周的利润情况记录:
日期
12日
13日
14日
15日
16日
17日
18日
当日利
润(万元)
0.20
0.17
0.23
0.21
0.23
0.18
0.25
根据上表,你估计利群超市该年5月份的总利润是( A )
(A)6.51万元
(B)6.4万元
(C)1.47万元
(D)5.88万元
6.小明记录了一星期每天的最高气温如下表,则这个星期每天的最高气温的中位数是(
B
)
星期
一
二
三
四
五
六
日
最高气温(℃)
22
24
23
25
24
22
21
A.22
℃
B.23
℃
C.24
℃
D.25
℃
7.若数据x1,x2,…,xn的众数为a,方差为b,则数据x1+2,x2+2,…,xn+2的众数、方差分别是( C )
(A)a,b
(B)a,b+2
(C)a+2,b
(D)a+2,b+2
8.若有①分析数据;②收集数据;③作出决策;④整理数据;⑤提出问题,则下列关于决策过程的排序正确的是( A )
A.⑤②④①③
B.⑤②①③④
C.④①③②⑤
D.⑤③②④①
9.若样本x1+1,x2+1,x3+1,……,xn+1的平均数为18,方差为2,则对于样本x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是( C )
A.平均数为18,方差为2
B.平均数为19,方差为3
C.平均数为19,方差为2
D.平均数为20,方差为4
10.一次统计八(2)班若干名学生每分钟跳绳次数的频数分布直方图如图所示.由这个直方图可知,这若干名学生平均每分钟跳绳的次数(结果精确到个位)是( C )
(A)数据不全无法计算
(B)103
(C)104
(D)105
填空题
11.在数据-1、0、4、5、8中插入一个数据x,使得该组数据的中位数是3,则x=____2______.
12.在一次爱心捐款中,某班有40名学生拿出自己的零花钱,有捐5元、10元、20元、50元的,如图反映了不同捐款的人数比例,那么这个班的学生平均每人捐款
16
元.
甲、乙两台机床生产同一种零件,并且每天产量相等,在6天中每天生产零件中的次品数依次是:甲:3,0,0,2,0,1;乙:1,0,2,1,0,2.则甲、乙两台机床中性能较稳定的是 甲 .
14.小明用s2=[(x1-3)2+(x2-3)2+…+(x10-3)2]计算一组数据的方差,那么x1+x2+x3+…+x10= .?
答案 30
15.某公司销售部有营销人员25人,销售部为了制订某种商品的销售定额,统计了这25人某月的销售量如下表:
每人销售量(单位:件)
600
500
400
350
300
200
人数(单位:人)
1
4
4
6
7
3
公司营销人员该月销售量的中位数是 .?
答案 350
16.下图是一组数据的折线统计图,这组数据的方差是 .(结果精确到0.1)?
答案 144.6
三、解答题
17.某校为了解全校2
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
解:(1)=(0.5×15+1.0×20+1.5×10+2.0×5)=1.05(小时),
这50名学生在这一天平均每人的课外阅读所用时间是1.05小时.
(2)2
000×=1
400(人),
所以全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有1
400人.
18.甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用上表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
解析 (1)a=7,b=7.5,c=4.2.
(2)根据题表中数据可知,甲和乙的平均成绩相等,乙的中位数大于甲的中位数,乙的众数大于甲的众数,说明乙的成绩好于甲的成绩,虽然乙的方差大于甲的方差,但乙的成绩呈上升趋势,故应选乙队员.(合理即可,答案不唯一)
19.在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二
69
97
91
69
98
100
99
100
90
100
99
69
97
100
99
94
79
99
98
79
(1)根据上述数据,将下列表格补充完整.
整理、描述数据:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
2
4
12
初二人数
2
2
1
15
分析数据:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
91.3
?
20%
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 (人);?
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
解:(1)由题意知初二年级的分数从小到大排列为69,69,69,79,
79,90,91,94,97,97,98,98,99,99,99,99,100,100,100,100,
所以初二年级成绩的中位数为97.5分,
补全表格如下:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
91.3
97.5 ?
20%
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数为300×25%+300×20%=135(人).
(3)初二年级掌握禁毒知识的总体水平较好,
∵初二年级的平均成绩比初一高,说明初二年级平均水平高,且初二年级成绩的中位数比初一大,说明初二年级的得高分人数多于初一,
∴初二年级掌握禁毒知识的总体水平较好.
20.爸爸为了解小明这学期在家的作息时间,随机挑选了某个星期对小明进行了观察,并记录了他娱乐的时间(单位:min):
日期
周一
周二
周三
周四
周五
周六
周日
娱乐时间
55
60
70
65
50
240
370
(1)分别计算小明这周内娱乐时间的平均数和中位数;
(2)应选中位数和平均数中的哪一个表示小明这一周的一般娱乐时间更好?为什么?
(3)能否用(2)的数据表示本学期小明在家娱乐的一般时间?为什么?
解析 (1)平均数=×(55+60+70+65+50+240+370)=130(min);中位数为65.
(2)选择中位数更好.
因为周六和周日的娱乐时间很长,可作为异常值,平均数受此影响较大,所以应选中位数.
(3)可以用这一中位数表示本学期小明在家娱乐的一般时间.因为这一周是随机抽取的,可以认为具有一定的代表性,所以这一周表示的娱乐时间平均水平的量──中位数可以用来估计整个学期的娱乐时间平均水平.若要更好地作出估计,则样本容量可以更大些.
21.某厂生产A,B两种产品,其单价随市场变化而进行相应的调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
并求得了A产品三次单价的平均数和方差:=5.9,=×[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=.
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;?
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
解析 (1)如图.
B产品第三次的单价比上一次的单价降低了25%.
(2)=×(3.5+4+3)=3.5,
=×[(3.5-3.5)2+(4-3.5)2+(3-3.5)2]=.
∵<,∴B产品的单价波动小.
(3)第四次调价后,对于A产品,这四次单价的中位数为=(元/件).
对于B产品,∵m>0,∴第四次单价大于3.
又∵×2-1=>,
∴第四次单价小于4(元/件),
∴×2-1=,∴m=25.
22.某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如下.
(1)求出下列成绩统计分析表中a,b的值;
组别
平均分
中位数
方差
合格率
优秀率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
解析 (1)由折线统计图可知,甲组成绩从小到大排列为3、6、6、6、6、6、7、9、9、10,
其中位数a=6,
乙组学生成绩的平均分b==7.2.
(2)∵甲组的中位数为6,乙组的中位数为7.5,而小英的成绩位于全班中上游,
∴小英属于甲组学生.
(3)①乙组的平均分高于甲组,即乙组的总体平均水平高;
②乙组的方差比甲组小,即乙组的成绩比甲组的成绩稳定.
23.一家商场张贴了下列海报:
好消息
在庆祝本店开业20周年之际,特举办“真情回报新老顾客”活动.本次活动共设奖金20万元,平均每份奖金200元,特等奖1万元!凡在本店购买物品金额满100元者均可参加抽奖.
一些顾客参加了抽奖,但没有一人的奖金超过50元,于是他们一起质问商场经理.商场经理拿出了下面一张表格:
奖金等级
特等奖
一等奖
二等奖
三等奖
四等奖
奖金额/元
10
000
6
000
1
000
50
10
中奖人数
3
10
87
350
550
你认为海报上写的“平均每份奖金200元”是否欺骗了顾客?用数据的哪种特征数最能代表获奖金额?说说你的理由.
解
每份奖金的平均数是
=200.
因此,海报上写的“平均每份奖金200元”并没有错.
但平均奖金由于受到极端值的影响,远远大于众数和中位数,作为数据的代表容易误导顾客.
这里用众数和中位数作为获奖金额的代表更合适,它们都是10.
24.某市某中学举行“中国梦·校园好声音”歌手大赛,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩统计情况如图所示.
(1)根据统计图填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,判断哪一个代表队选手的成绩较为稳定.
解析 (1)填表:初中部平均数为85,众数为85;高中部中位数为80.
(2)初中代表队成绩好些.因为两个队成绩的平均数相同,初中部代表部成绩的中位数较高,所以在平均数相同的情况下,中位数高的代表队成绩好些.
(3)==70,
==160,
∵<,∴初中代表队选手的成绩较为稳定.
数据的分析
单元检测卷
一、选择题
1.自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是(
)
A.3
B.4
C.5
D.6
2.已知一组数据x1,x2,x3的平均数为6,则数据x1+1,x2+1,x3+1的平均数为(
)
A.6 B.7 C.9 D.12
3.要判断某同学的数学考试成绩是否稳定,那么需要知道他最近几次数学考试成绩的(
)
A.方差
B.众数
C.平均数
D.中位数
4.某居民小区开展节约用电活动,对该小区100户家庭的节电量情况进行了统计,4月份与3月份相比,节电情况如下表,则4月份这100户节电量的平均数、中位数、众数分别是(
)
节电量(千瓦时)
20
30
40
50
户数
10
40
30
20
A.35、35、30
B.25、30、20
C.36、35、30
D.36、30、30
5.下表是利群超市5月份一周的利润情况记录:
日期
12日
13日
14日
15日
16日
17日
18日
当日利
润(万元)
0.20
0.17
0.23
0.21
0.23
0.18
0.25
根据上表,你估计利群超市该年5月份的总利润是(
)
(A)6.51万元
(B)6.4万元
(C)1.47万元
(D)5.88万元
6.小明记录了一星期每天的最高气温如下表,则这个星期每天的最高气温的中位数是(
)
星期
一
二
三
四
五
六
日
最高气温(℃)
22
24
23
25
24
22
21
A.22
℃
B.23
℃
C.24
℃
D.25
℃
7.若数据x1,x2,…,xn的众数为a,方差为b,则数据x1+2,x2+2,…,xn+2的众数、方差分别是(
)
(A)a,b
(B)a,b+2
(C)a+2,b
(D)a+2,b+2
8.若有①分析数据;②收集数据;③作出决策;④整理数据;⑤提出问题,则下列关于决策过程的排序正确的是(
)
A.⑤②④①③
B.⑤②①③④
C.④①③②⑤
D.⑤③②④①
9.若样本x1+1,x2+1,x3+1,……,xn+1的平均数为18,方差为2,则对于样本x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是(
)
A.平均数为18,方差为2
B.平均数为19,方差为3
C.平均数为19,方差为2
D.平均数为20,方差为4
10.一次统计八(2)班若干名学生每分钟跳绳次数的频数分布直方图如图所示.由这个直方图可知,这若干名学生平均每分钟跳绳的次数(结果精确到个位)是(
)
(A)数据不全无法计算
(B)103
(C)104
(D)105
填空题
11.在数据-1、0、4、5、8中插入一个数据x,使得该组数据的中位数是3,则x=_________.
12.在一次爱心捐款中,某班有40名学生拿出自己的零花钱,有捐5元、10元、20元、50元的,如图反映了不同捐款的人数比例,那么这个班的学生平均每人捐款
元.
甲、乙两台机床生产同一种零件,并且每天产量相等,在6天中每天生产零件中的次品数依次是:甲:3,0,0,2,0,1;乙:1,0,2,1,0,2.则甲、乙两台机床中性能较稳定的是 .
14.小明用s2=[(x1-3)2+(x2-3)2+…+(x10-3)2]计算一组数据的方差,那么x1+x2+x3+…+x10= .?
15.某公司销售部有营销人员25人,销售部为了制订某种商品的销售定额,统计了这25人某月的销售量如下表:
每人销售量(单位:件)
600
500
400
350
300
200
人数(单位:人)
1
4
4
6
7
3
公司营销人员该月销售量的中位数是 .?
16.下图是一组数据的折线统计图,这组数据的方差是 .(结果精确到0.1)?
三、解答题
17.某校为了解全校2
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
18.甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用上表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
19.在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二
69
97
91
69
98
100
99
100
90
100
99
69
97
100
99
94
79
99
98
79
(1)根据上述数据,将下列表格补充完整.
整理、描述数据:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
2
4
12
初二人数
2
2
1
15
分析数据:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
91.3
?
20%
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 (人);?
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
20.爸爸为了解小明这学期在家的作息时间,随机挑选了某个星期对小明进行了观察,并记录了他娱乐的时间(单位:min):
日期
周一
周二
周三
周四
周五
周六
周日
娱乐时间
55
60
70
65
50
240
370
(1)分别计算小明这周内娱乐时间的平均数和中位数;
(2)应选中位数和平均数中的哪一个表示小明这一周的一般娱乐时间更好?为什么?
(3)能否用(2)的数据表示本学期小明在家娱乐的一般时间?为什么?
21.某厂生产A,B两种产品,其单价随市场变化而进行相应的调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
并求得了A产品三次单价的平均数和方差:=5.9,=×[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=.
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;?
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
22.某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如下.
(1)求出下列成绩统计分析表中a,b的值;
组别
平均分
中位数
方差
合格率
优秀率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
23.一家商场张贴了下列海报:
好消息
在庆祝本店开业20周年之际,特举办“真情回报新老顾客”活动.本次活动共设奖金20万元,平均每份奖金200元,特等奖1万元!凡在本店购买物品金额满100元者均可参加抽奖.
一些顾客参加了抽奖,但没有一人的奖金超过50元,于是他们一起质问商场经理.商场经理拿出了下面一张表格:
奖金等级
特等奖
一等奖
二等奖
三等奖
四等奖
奖金额/元
10
000
6
000
1
000
50
10
中奖人数
3
10
87
350
550
你认为海报上写的“平均每份奖金200元”是否欺骗了顾客?用数据的哪种特征数最能代表获奖金额?说说你的理由.
24.某市某中学举行“中国梦·校园好声音”歌手大赛,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩统计情况如图所示.
(1)根据统计图填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,判断哪一个代表队选手的成绩较为稳定.
参考答案
一、选择题
1.自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是( B )
A.3
B.4
C.5
D.6
2.已知一组数据x1,x2,x3的平均数为6,则数据x1+1,x2+1,x3+1的平均数为( B )
A.6 B.7 C.9 D.12
3.要判断某同学的数学考试成绩是否稳定,那么需要知道他最近几次数学考试成绩的( A )
A.方差
B.众数
C.平均数
D.中位数
4.某居民小区开展节约用电活动,对该小区100户家庭的节电量情况进行了统计,4月份与3月份相比,节电情况如下表,则4月份这100户节电量的平均数、中位数、众数分别是( C )
节电量(千瓦时)
20
30
40
50
户数
10
40
30
20
A.35、35、30
B.25、30、20
C.36、35、30
D.36、30、30
5.下表是利群超市5月份一周的利润情况记录:
日期
12日
13日
14日
15日
16日
17日
18日
当日利
润(万元)
0.20
0.17
0.23
0.21
0.23
0.18
0.25
根据上表,你估计利群超市该年5月份的总利润是( A )
(A)6.51万元
(B)6.4万元
(C)1.47万元
(D)5.88万元
6.小明记录了一星期每天的最高气温如下表,则这个星期每天的最高气温的中位数是(
B
)
星期
一
二
三
四
五
六
日
最高气温(℃)
22
24
23
25
24
22
21
A.22
℃
B.23
℃
C.24
℃
D.25
℃
7.若数据x1,x2,…,xn的众数为a,方差为b,则数据x1+2,x2+2,…,xn+2的众数、方差分别是( C )
(A)a,b
(B)a,b+2
(C)a+2,b
(D)a+2,b+2
8.若有①分析数据;②收集数据;③作出决策;④整理数据;⑤提出问题,则下列关于决策过程的排序正确的是( A )
A.⑤②④①③
B.⑤②①③④
C.④①③②⑤
D.⑤③②④①
9.若样本x1+1,x2+1,x3+1,……,xn+1的平均数为18,方差为2,则对于样本x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是( C )
A.平均数为18,方差为2
B.平均数为19,方差为3
C.平均数为19,方差为2
D.平均数为20,方差为4
10.一次统计八(2)班若干名学生每分钟跳绳次数的频数分布直方图如图所示.由这个直方图可知,这若干名学生平均每分钟跳绳的次数(结果精确到个位)是( C )
(A)数据不全无法计算
(B)103
(C)104
(D)105
填空题
11.在数据-1、0、4、5、8中插入一个数据x,使得该组数据的中位数是3,则x=____2______.
12.在一次爱心捐款中,某班有40名学生拿出自己的零花钱,有捐5元、10元、20元、50元的,如图反映了不同捐款的人数比例,那么这个班的学生平均每人捐款
16
元.
甲、乙两台机床生产同一种零件,并且每天产量相等,在6天中每天生产零件中的次品数依次是:甲:3,0,0,2,0,1;乙:1,0,2,1,0,2.则甲、乙两台机床中性能较稳定的是 甲 .
14.小明用s2=[(x1-3)2+(x2-3)2+…+(x10-3)2]计算一组数据的方差,那么x1+x2+x3+…+x10= .?
答案 30
15.某公司销售部有营销人员25人,销售部为了制订某种商品的销售定额,统计了这25人某月的销售量如下表:
每人销售量(单位:件)
600
500
400
350
300
200
人数(单位:人)
1
4
4
6
7
3
公司营销人员该月销售量的中位数是 .?
答案 350
16.下图是一组数据的折线统计图,这组数据的方差是 .(结果精确到0.1)?
答案 144.6
三、解答题
17.某校为了解全校2
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
解:(1)=(0.5×15+1.0×20+1.5×10+2.0×5)=1.05(小时),
这50名学生在这一天平均每人的课外阅读所用时间是1.05小时.
(2)2
000×=1
400(人),
所以全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有1
400人.
18.甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)写出表格中a,b,c的值;
(2)分别运用上表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
解析 (1)a=7,b=7.5,c=4.2.
(2)根据题表中数据可知,甲和乙的平均成绩相等,乙的中位数大于甲的中位数,乙的众数大于甲的众数,说明乙的成绩好于甲的成绩,虽然乙的方差大于甲的方差,但乙的成绩呈上升趋势,故应选乙队员.(合理即可,答案不唯一)
19.在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二
69
97
91
69
98
100
99
100
90
100
99
69
97
100
99
94
79
99
98
79
(1)根据上述数据,将下列表格补充完整.
整理、描述数据:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
2
4
12
初二人数
2
2
1
15
分析数据:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
91.3
?
20%
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 (人);?
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
解:(1)由题意知初二年级的分数从小到大排列为69,69,69,79,
79,90,91,94,97,97,98,98,99,99,99,99,100,100,100,100,
所以初二年级成绩的中位数为97.5分,
补全表格如下:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
91.3
97.5 ?
20%
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数为300×25%+300×20%=135(人).
(3)初二年级掌握禁毒知识的总体水平较好,
∵初二年级的平均成绩比初一高,说明初二年级平均水平高,且初二年级成绩的中位数比初一大,说明初二年级的得高分人数多于初一,
∴初二年级掌握禁毒知识的总体水平较好.
20.爸爸为了解小明这学期在家的作息时间,随机挑选了某个星期对小明进行了观察,并记录了他娱乐的时间(单位:min):
日期
周一
周二
周三
周四
周五
周六
周日
娱乐时间
55
60
70
65
50
240
370
(1)分别计算小明这周内娱乐时间的平均数和中位数;
(2)应选中位数和平均数中的哪一个表示小明这一周的一般娱乐时间更好?为什么?
(3)能否用(2)的数据表示本学期小明在家娱乐的一般时间?为什么?
解析 (1)平均数=×(55+60+70+65+50+240+370)=130(min);中位数为65.
(2)选择中位数更好.
因为周六和周日的娱乐时间很长,可作为异常值,平均数受此影响较大,所以应选中位数.
(3)可以用这一中位数表示本学期小明在家娱乐的一般时间.因为这一周是随机抽取的,可以认为具有一定的代表性,所以这一周表示的娱乐时间平均水平的量──中位数可以用来估计整个学期的娱乐时间平均水平.若要更好地作出估计,则样本容量可以更大些.
21.某厂生产A,B两种产品,其单价随市场变化而进行相应的调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
并求得了A产品三次单价的平均数和方差:=5.9,=×[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=.
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;?
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
解析 (1)如图.
B产品第三次的单价比上一次的单价降低了25%.
(2)=×(3.5+4+3)=3.5,
=×[(3.5-3.5)2+(4-3.5)2+(3-3.5)2]=.
∵<,∴B产品的单价波动小.
(3)第四次调价后,对于A产品,这四次单价的中位数为=(元/件).
对于B产品,∵m>0,∴第四次单价大于3.
又∵×2-1=>,
∴第四次单价小于4(元/件),
∴×2-1=,∴m=25.
22.某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如下.
(1)求出下列成绩统计分析表中a,b的值;
组别
平均分
中位数
方差
合格率
优秀率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
解析 (1)由折线统计图可知,甲组成绩从小到大排列为3、6、6、6、6、6、7、9、9、10,
其中位数a=6,
乙组学生成绩的平均分b==7.2.
(2)∵甲组的中位数为6,乙组的中位数为7.5,而小英的成绩位于全班中上游,
∴小英属于甲组学生.
(3)①乙组的平均分高于甲组,即乙组的总体平均水平高;
②乙组的方差比甲组小,即乙组的成绩比甲组的成绩稳定.
23.一家商场张贴了下列海报:
好消息
在庆祝本店开业20周年之际,特举办“真情回报新老顾客”活动.本次活动共设奖金20万元,平均每份奖金200元,特等奖1万元!凡在本店购买物品金额满100元者均可参加抽奖.
一些顾客参加了抽奖,但没有一人的奖金超过50元,于是他们一起质问商场经理.商场经理拿出了下面一张表格:
奖金等级
特等奖
一等奖
二等奖
三等奖
四等奖
奖金额/元
10
000
6
000
1
000
50
10
中奖人数
3
10
87
350
550
你认为海报上写的“平均每份奖金200元”是否欺骗了顾客?用数据的哪种特征数最能代表获奖金额?说说你的理由.
解
每份奖金的平均数是
=200.
因此,海报上写的“平均每份奖金200元”并没有错.
但平均奖金由于受到极端值的影响,远远大于众数和中位数,作为数据的代表容易误导顾客.
这里用众数和中位数作为获奖金额的代表更合适,它们都是10.
24.某市某中学举行“中国梦·校园好声音”歌手大赛,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩统计情况如图所示.
(1)根据统计图填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,判断哪一个代表队选手的成绩较为稳定.
解析 (1)填表:初中部平均数为85,众数为85;高中部中位数为80.
(2)初中代表队成绩好些.因为两个队成绩的平均数相同,初中部代表部成绩的中位数较高,所以在平均数相同的情况下,中位数高的代表队成绩好些.
(3)==70,
==160,
∵<,∴初中代表队选手的成绩较为稳定.
