人教版八年级数学下册 20.1----20.2 课后巩固训练含答案
文档属性
| 名称 | 人教版八年级数学下册 20.1----20.2 课后巩固训练含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 300.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-05 08:19:07 | ||
图片预览


文档简介
人教版八年级数学下册第二十章
20.1----20.2
课后巩固训练
一、选择题
1.已知x1、x2、x3的平均数是,那么3x1+5,3x2+5,3x3+5的平均数是(
)
A.
B.3
C.3+5
D.不能确定
2.自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是(
)
A.3
B.4
C.5
D.6
3.已知一组数据x1,x2,x3如下表,那么另一组数据2x1-1,2x2-1,2x3-1的平均数和方差分别是(
)
x1
x2
x3
1
2
3
A.2, B.3,
C.3, D.3,
4.为了满足顾客的需求,某商场将5
kg奶糖,3
kg酥心糖和2
kg水果糖混合成什锦糖出售.已知奶糖的售价为每千克40元,酥心糖为每千克20元,水果糖为每千克15元,则什锦糖的售价应为每千克(
)
(A)25元
(B)28.5元
(C)29元
(D)34.5元
5.实施新课改以来,某班学生经常采用“小组合作学习”的方式进行学习,值周班长小兵每周对各小组合作学习的情况进行综合评分,下表是其中一周的评分结果.
组别
一
二
三
四
五
六
七
分值
90
96
89
90
91
85
90
“分值”这组数据的中位数和众数分别是(
)
A.89,90
B.90,90
C.88,95
D.90,95
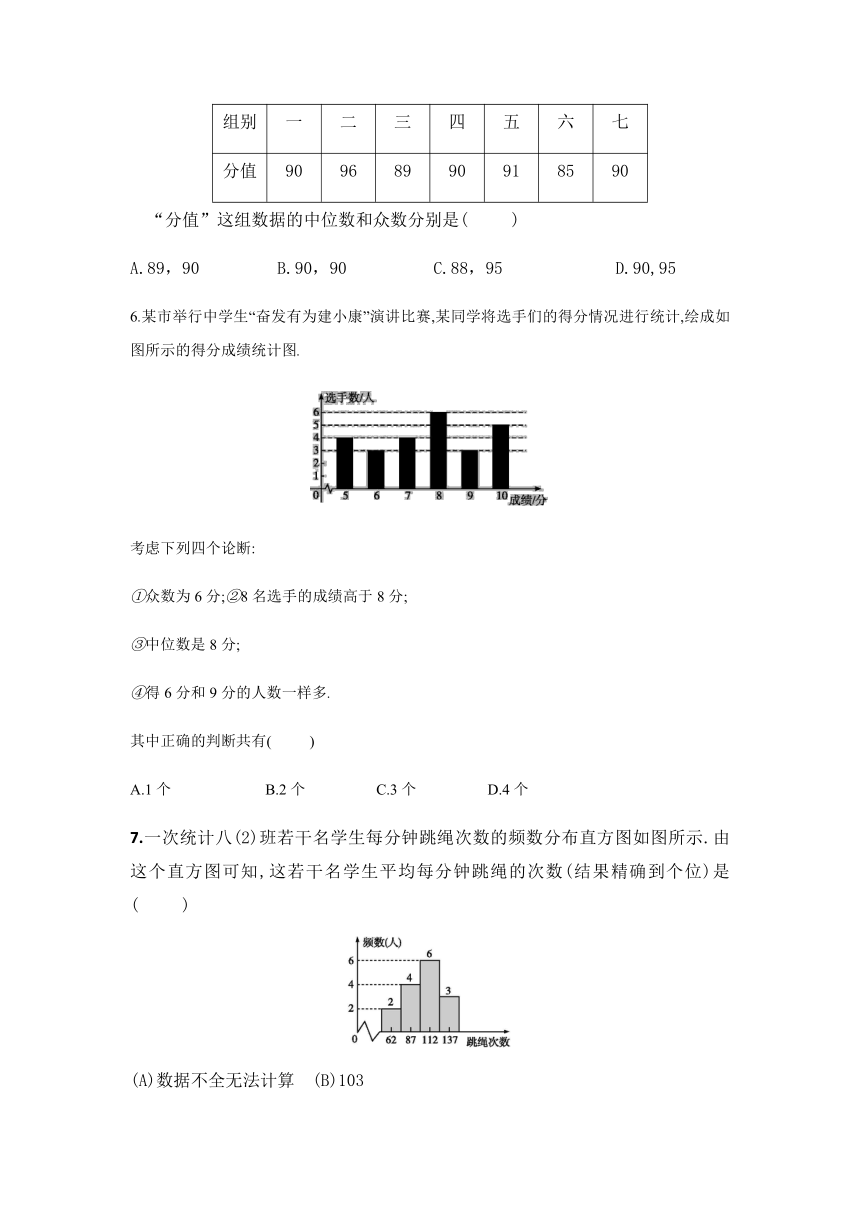
6.某市举行中学生“奋发有为建小康”演讲比赛,某同学将选手们的得分情况进行统计,绘成如图所示的得分成绩统计图.
考虑下列四个论断:
①众数为6分;②8名选手的成绩高于8分;
③中位数是8分;
④得6分和9分的人数一样多.
其中正确的判断共有(
)
A.1个
B.2个
C.3个
D.4个
7.一次统计八(2)班若干名学生每分钟跳绳次数的频数分布直方图如图所示.由这个直方图可知,这若干名学生平均每分钟跳绳的次数(结果精确到个位)是(
)
(A)数据不全无法计算
(B)103
(C)104
(D)105
8.若一组数据1,2,3,4,x的平均数与中位数相同,则实数x的值不可能是(
)
A.0 B.2.5 C.3 D.5
9.若样本x1+1,x2+1,x3+1,……,xn+1的平均数为18,方差为2,则对于样本x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是(
)
A.平均数为18,方差为2
B.平均数为19,方差为3
C.平均数为19,方差为2
D.平均数为20,方差为4
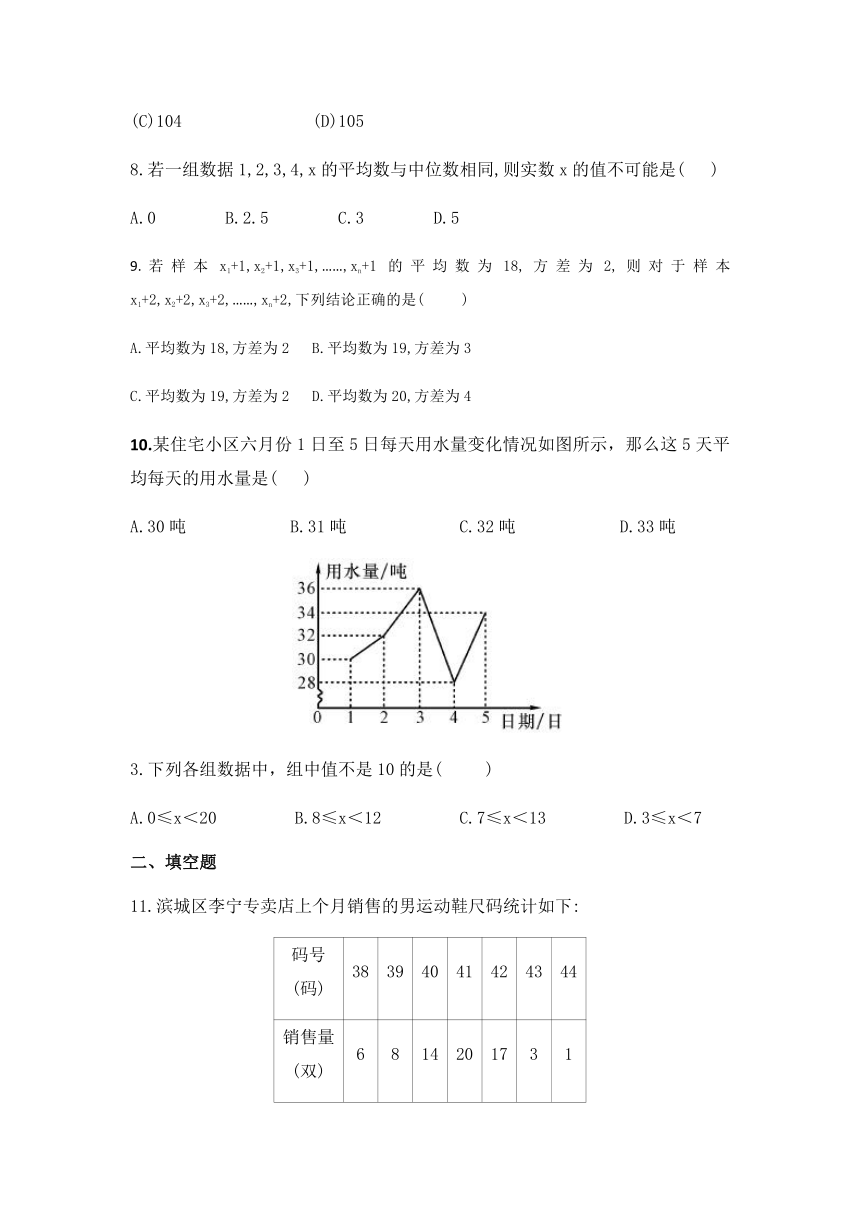
10.某住宅小区六月份1日至5日每天用水量变化情况如图所示,那么这5天平均每天的用水量是(
)
A.30吨
B.31吨
C.32吨
D.33吨
3.下列各组数据中,组中值不是10的是(
)
A.0≤x<20
B.8≤x<12
C.7≤x<13
D.3≤x<7
填空题
11.滨城区李宁专卖店上个月销售的男运动鞋尺码统计如下:
码号(码)
38
39
40
41
42
43
44
销售量(双)
6
8
14
20
17
3
1
这组统计数据的众数是 码.?
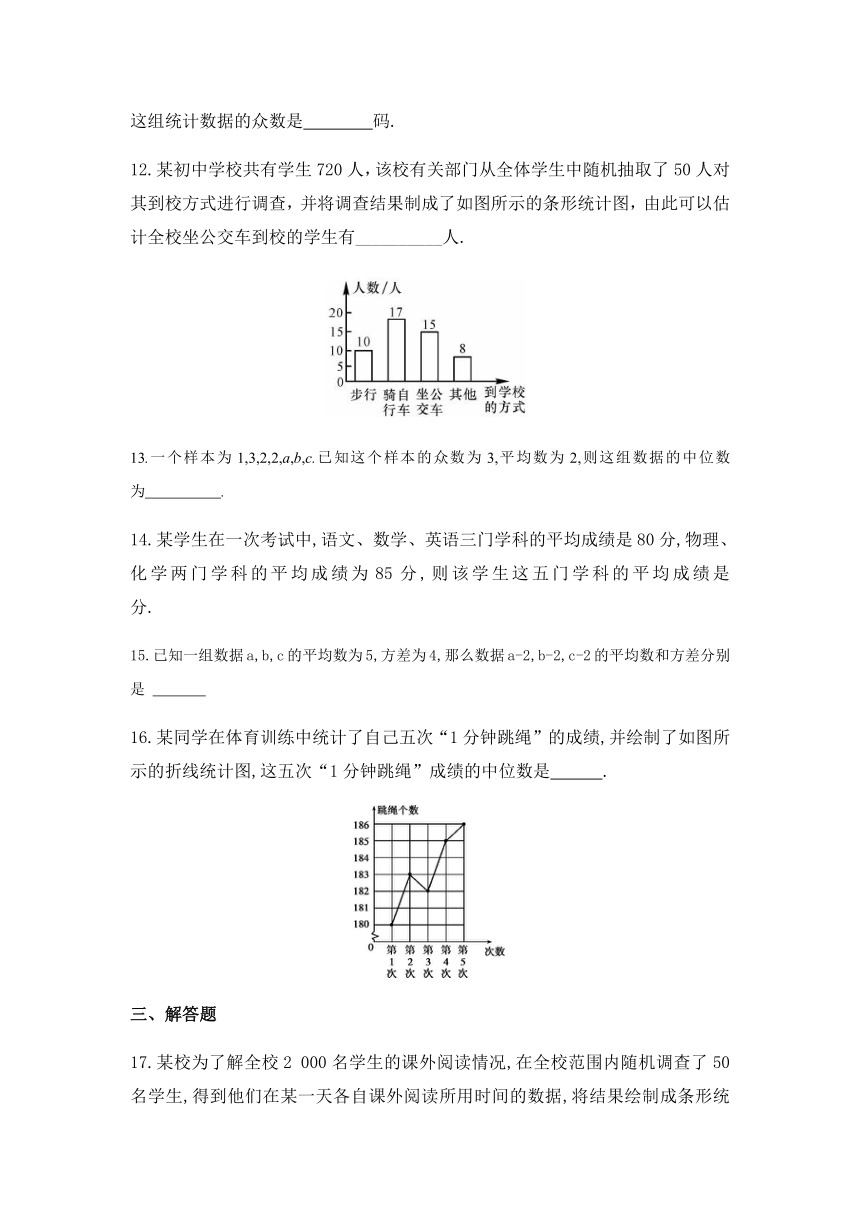
12.某初中学校共有学生720人,该校有关部门从全体学生中随机抽取了50人对其到校方式进行调查,并将调查结果制成了如图所示的条形统计图,由此可以估计全校坐公交车到校的学生有__________人.
13.一个样本为1,3,2,2,a,b,c.已知这个样本的众数为3,平均数为2,则这组数据的中位数为 .?
14.某学生在一次考试中,语文、数学、英语三门学科的平均成绩是80分,物理、化学两门学科的平均成绩为85分,则该学生这五门学科的平均成绩是 分.?
15.已知一组数据a,b,c的平均数为5,方差为4,那么数据a-2,b-2,c-2的平均数和方差分别是
16.某同学在体育训练中统计了自己五次“1分钟跳绳”的成绩,并绘制了如图所示的折线统计图,这五次“1分钟跳绳”成绩的中位数是 .?
三、解答题
17.某校为了解全校2
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
18.某厂生产A,B两种产品,其单价随市场变化而进行相应的调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
并求得了A产品三次单价的平均数和方差:=5.9,=×[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=.
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;?
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
19.在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二
69
97
91
69
98
100
99
100
90
100
99
69
97
100
99
94
79
99
98
79
(1)根据上述数据,将下列表格补充完整.
整理、描述数据:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
2
4
12
初二人数
2
2
1
15
分析数据:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
91.3
?
20%
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 (人);?
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
20.某校要从九年级(一)班和(二)班中各选取10名女同学组成礼仪队,选取的两班女生的身高如下:(单位:厘米)
(一)班:168
167
170
165
168
166
171
168
167
170
(二)班:165
167
169
170
165
168
170
171
168
167
(1)补充完成下面的统计分析表:
班级
平均数
方差
中位数
(一)班
168
168
(二)班
168
3.8
(2)请选一个合适的统计量作为选择标准,说明哪一个班能被选取.
21.学校广播站要招聘一名播音员,测试形象、知识面、普通话三个项目,按形象占10%,知识面占40%,普通话占50%计算加权平均数,作为最后评定的总成绩.
李文和孔明两位同学的各项成绩如表:
项目
选手
形象
知识面
普通话
李文
70
80
88
孔明
80
75
x
(1)计算李文同学的总成绩;
(2)若孔明同学要在总成绩上超过李文同学,则他的普通话成绩x应超过多少分?
参考答案
一、选择题
1.已知x1、x2、x3的平均数是,那么3x1+5,3x2+5,3x3+5的平均数是(
C
)
A.
B.3
C.3+5
D.不能确定
2.自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是( B )
A.3
B.4
C.5
D.6
3.已知一组数据x1,x2,x3如下表,那么另一组数据2x1-1,2x2-1,2x3-1的平均数和方差分别是(
C )
x1
x2
x3
1
2
3
A.2, B.3,
C.3, D.3,
4.为了满足顾客的需求,某商场将5
kg奶糖,3
kg酥心糖和2
kg水果糖混合成什锦糖出售.已知奶糖的售价为每千克40元,酥心糖为每千克20元,水果糖为每千克15元,则什锦糖的售价应为每千克( C )
(A)25元
(B)28.5元
(C)29元
(D)34.5元
5.实施新课改以来,某班学生经常采用“小组合作学习”的方式进行学习,值周班长小兵每周对各小组合作学习的情况进行综合评分,下表是其中一周的评分结果.
组别
一
二
三
四
五
六
七
分值
90
96
89
90
91
85
90
“分值”这组数据的中位数和众数分别是(
B
)
A.89,90
B.90,90
C.88,95
D.90,95
6.某市举行中学生“奋发有为建小康”演讲比赛,某同学将选手们的得分情况进行统计,绘成如图所示的得分成绩统计图.
考虑下列四个论断:
①众数为6分;②8名选手的成绩高于8分;
③中位数是8分;
④得6分和9分的人数一样多.
其中正确的判断共有( B
)
A.1个
B.2个
C.3个
D.4个
7.一次统计八(2)班若干名学生每分钟跳绳次数的频数分布直方图如图所示.由这个直方图可知,这若干名学生平均每分钟跳绳的次数(结果精确到个位)是( C )
(A)数据不全无法计算
(B)103
(C)104
(D)105
8.若一组数据1,2,3,4,x的平均数与中位数相同,则实数x的值不可能是( C )
A.0 B.2.5 C.3 D.5
9.若样本x1+1,x2+1,x3+1,……,xn+1的平均数为18,方差为2,则对于样本x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是(
)
A.平均数为18,方差为2
B.平均数为19,方差为3
C.平均数为19,方差为2
D.平均数为20,方差为4
10.某住宅小区六月份1日至5日每天用水量变化情况如图所示,那么这5天平均每天的用水量是(
C
)
A.30吨
B.31吨
C.32吨
D.33吨
3.下列各组数据中,组中值不是10的是(
D
)
A.0≤x<20
B.8≤x<12
C.7≤x<13
D.3≤x<7
填空题
11.滨城区李宁专卖店上个月销售的男运动鞋尺码统计如下:
码号(码)
38
39
40
41
42
43
44
销售量(双)
6
8
14
20
17
3
1
这组统计数据的众数是 40 码.?
12.某初中学校共有学生720人,该校有关部门从全体学生中随机抽取了50人对其到校方式进行调查,并将调查结果制成了如图所示的条形统计图,由此可以估计全校坐公交车到校的学生有_____7_____人.
13.一个样本为1,3,2,2,a,b,c.已知这个样本的众数为3,平均数为2,则这组数据的中位数为 2 .?
14.某学生在一次考试中,语文、数学、英语三门学科的平均成绩是80分,物理、化学两门学科的平均成绩为85分,则该学生这五门学科的平均成绩是 82 分.?
15.已知一组数据a,b,c的平均数为5,方差为4,那么数据a-2,b-2,c-2的平均数和方差分别是
答案3,4
16.某同学在体育训练中统计了自己五次“1分钟跳绳”的成绩,并绘制了如图所示的折线统计图,这五次“1分钟跳绳”成绩的中位数是 183 .?
三、解答题
17.某校为了解全校2
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
解:(1)=(0.5×15+1.0×20+1.5×10+2.0×5)=1.05(小时),
这50名学生在这一天平均每人的课外阅读所用时间是1.05小时.
(2)2
000×=1
400(人),
所以全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有1
400人.
18.某厂生产A,B两种产品,其单价随市场变化而进行相应的调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
并求得了A产品三次单价的平均数和方差:=5.9,=×[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=.
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;?
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
解析 (1)如图.
B产品第三次的单价比上一次的单价降低了25%.
(2)=×(3.5+4+3)=3.5,
=×[(3.5-3.5)2+(4-3.5)2+(3-3.5)2]=.
∵<,∴B产品的单价波动小.
(3)第四次调价后,对于A产品,这四次单价的中位数为=(元/件).
对于B产品,∵m>0,∴第四次单价大于3.
又∵×2-1=>,
∴第四次单价小于4(元/件),
∴×2-1=,∴m=25.
18.在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二
69
97
91
69
98
100
99
100
90
100
99
69
97
100
99
94
79
99
98
79
(1)根据上述数据,将下列表格补充完整.
整理、描述数据:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
2
4
12
初二人数
2
2
1
15
分析数据:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
91.3
?
20%
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 (人);?
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
解:(1)由题意知初二年级的分数从小到大排列为69,69,69,79,
79,90,91,94,97,97,98,98,99,99,99,99,100,100,100,100,
所以初二年级成绩的中位数为97.5分,
补全表格如下:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
91.3
97.5 ?
20%
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数为300×25%+300×20%=135(人).
(3)初二年级掌握禁毒知识的总体水平较好,
∵初二年级的平均成绩比初一高,说明初二年级平均水平高,且初二年级成绩的中位数比初一大,说明初二年级的得高分人数多于初一,
∴初二年级掌握禁毒知识的总体水平较好.
20.某校要从九年级(一)班和(二)班中各选取10名女同学组成礼仪队,选取的两班女生的身高如下:(单位:厘米)
(一)班:168
167
170
165
168
166
171
168
167
170
(二)班:165
167
169
170
165
168
170
171
168
167
(1)补充完成下面的统计分析表:
班级
平均数
方差
中位数
(一)班
168
168
(二)班
168
3.8
(2)请选一个合适的统计量作为选择标准,说明哪一个班能被选取.
解(1)3.2;168.
(2)选择方差作标准,
∵(一)班方差<(二)班方差,
∴(一)班能被选取.
21.学校广播站要招聘一名播音员,测试形象、知识面、普通话三个项目,按形象占10%,知识面占40%,普通话占50%计算加权平均数,作为最后评定的总成绩.
李文和孔明两位同学的各项成绩如表:
项目
选手
形象
知识面
普通话
李文
70
80
88
孔明
80
75
x
(1)计算李文同学的总成绩;
(2)若孔明同学要在总成绩上超过李文同学,则他的普通话成绩x应超过多少分?
解:(1)李文同学的总成绩为
70×10%+80×40%+88×50%=83(分).
(2)孔明同学的总成绩为80×10%+75×40%+50%·x.
根据题意,得80×10%+75×40%+50%·x>83,解得x>90.
答:若孔明同学要在总成绩上超过李文同学,则他的普通话成绩应超过90分.
20.1----20.2
课后巩固训练
一、选择题
1.已知x1、x2、x3的平均数是,那么3x1+5,3x2+5,3x3+5的平均数是(
)
A.
B.3
C.3+5
D.不能确定
2.自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是(
)
A.3
B.4
C.5
D.6
3.已知一组数据x1,x2,x3如下表,那么另一组数据2x1-1,2x2-1,2x3-1的平均数和方差分别是(
)
x1
x2
x3
1
2
3
A.2, B.3,
C.3, D.3,
4.为了满足顾客的需求,某商场将5
kg奶糖,3
kg酥心糖和2
kg水果糖混合成什锦糖出售.已知奶糖的售价为每千克40元,酥心糖为每千克20元,水果糖为每千克15元,则什锦糖的售价应为每千克(
)
(A)25元
(B)28.5元
(C)29元
(D)34.5元
5.实施新课改以来,某班学生经常采用“小组合作学习”的方式进行学习,值周班长小兵每周对各小组合作学习的情况进行综合评分,下表是其中一周的评分结果.
组别
一
二
三
四
五
六
七
分值
90
96
89
90
91
85
90
“分值”这组数据的中位数和众数分别是(
)
A.89,90
B.90,90
C.88,95
D.90,95
6.某市举行中学生“奋发有为建小康”演讲比赛,某同学将选手们的得分情况进行统计,绘成如图所示的得分成绩统计图.
考虑下列四个论断:
①众数为6分;②8名选手的成绩高于8分;
③中位数是8分;
④得6分和9分的人数一样多.
其中正确的判断共有(
)
A.1个
B.2个
C.3个
D.4个
7.一次统计八(2)班若干名学生每分钟跳绳次数的频数分布直方图如图所示.由这个直方图可知,这若干名学生平均每分钟跳绳的次数(结果精确到个位)是(
)
(A)数据不全无法计算
(B)103
(C)104
(D)105
8.若一组数据1,2,3,4,x的平均数与中位数相同,则实数x的值不可能是(
)
A.0 B.2.5 C.3 D.5
9.若样本x1+1,x2+1,x3+1,……,xn+1的平均数为18,方差为2,则对于样本x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是(
)
A.平均数为18,方差为2
B.平均数为19,方差为3
C.平均数为19,方差为2
D.平均数为20,方差为4
10.某住宅小区六月份1日至5日每天用水量变化情况如图所示,那么这5天平均每天的用水量是(
)
A.30吨
B.31吨
C.32吨
D.33吨
3.下列各组数据中,组中值不是10的是(
)
A.0≤x<20
B.8≤x<12
C.7≤x<13
D.3≤x<7
填空题
11.滨城区李宁专卖店上个月销售的男运动鞋尺码统计如下:
码号(码)
38
39
40
41
42
43
44
销售量(双)
6
8
14
20
17
3
1
这组统计数据的众数是 码.?
12.某初中学校共有学生720人,该校有关部门从全体学生中随机抽取了50人对其到校方式进行调查,并将调查结果制成了如图所示的条形统计图,由此可以估计全校坐公交车到校的学生有__________人.
13.一个样本为1,3,2,2,a,b,c.已知这个样本的众数为3,平均数为2,则这组数据的中位数为 .?
14.某学生在一次考试中,语文、数学、英语三门学科的平均成绩是80分,物理、化学两门学科的平均成绩为85分,则该学生这五门学科的平均成绩是 分.?
15.已知一组数据a,b,c的平均数为5,方差为4,那么数据a-2,b-2,c-2的平均数和方差分别是
16.某同学在体育训练中统计了自己五次“1分钟跳绳”的成绩,并绘制了如图所示的折线统计图,这五次“1分钟跳绳”成绩的中位数是 .?
三、解答题
17.某校为了解全校2
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
18.某厂生产A,B两种产品,其单价随市场变化而进行相应的调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
并求得了A产品三次单价的平均数和方差:=5.9,=×[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=.
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;?
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
19.在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二
69
97
91
69
98
100
99
100
90
100
99
69
97
100
99
94
79
99
98
79
(1)根据上述数据,将下列表格补充完整.
整理、描述数据:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
2
4
12
初二人数
2
2
1
15
分析数据:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
91.3
?
20%
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 (人);?
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
20.某校要从九年级(一)班和(二)班中各选取10名女同学组成礼仪队,选取的两班女生的身高如下:(单位:厘米)
(一)班:168
167
170
165
168
166
171
168
167
170
(二)班:165
167
169
170
165
168
170
171
168
167
(1)补充完成下面的统计分析表:
班级
平均数
方差
中位数
(一)班
168
168
(二)班
168
3.8
(2)请选一个合适的统计量作为选择标准,说明哪一个班能被选取.
21.学校广播站要招聘一名播音员,测试形象、知识面、普通话三个项目,按形象占10%,知识面占40%,普通话占50%计算加权平均数,作为最后评定的总成绩.
李文和孔明两位同学的各项成绩如表:
项目
选手
形象
知识面
普通话
李文
70
80
88
孔明
80
75
x
(1)计算李文同学的总成绩;
(2)若孔明同学要在总成绩上超过李文同学,则他的普通话成绩x应超过多少分?
参考答案
一、选择题
1.已知x1、x2、x3的平均数是,那么3x1+5,3x2+5,3x3+5的平均数是(
C
)
A.
B.3
C.3+5
D.不能确定
2.自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是( B )
A.3
B.4
C.5
D.6
3.已知一组数据x1,x2,x3如下表,那么另一组数据2x1-1,2x2-1,2x3-1的平均数和方差分别是(
C )
x1
x2
x3
1
2
3
A.2, B.3,
C.3, D.3,
4.为了满足顾客的需求,某商场将5
kg奶糖,3
kg酥心糖和2
kg水果糖混合成什锦糖出售.已知奶糖的售价为每千克40元,酥心糖为每千克20元,水果糖为每千克15元,则什锦糖的售价应为每千克( C )
(A)25元
(B)28.5元
(C)29元
(D)34.5元
5.实施新课改以来,某班学生经常采用“小组合作学习”的方式进行学习,值周班长小兵每周对各小组合作学习的情况进行综合评分,下表是其中一周的评分结果.
组别
一
二
三
四
五
六
七
分值
90
96
89
90
91
85
90
“分值”这组数据的中位数和众数分别是(
B
)
A.89,90
B.90,90
C.88,95
D.90,95
6.某市举行中学生“奋发有为建小康”演讲比赛,某同学将选手们的得分情况进行统计,绘成如图所示的得分成绩统计图.
考虑下列四个论断:
①众数为6分;②8名选手的成绩高于8分;
③中位数是8分;
④得6分和9分的人数一样多.
其中正确的判断共有( B
)
A.1个
B.2个
C.3个
D.4个
7.一次统计八(2)班若干名学生每分钟跳绳次数的频数分布直方图如图所示.由这个直方图可知,这若干名学生平均每分钟跳绳的次数(结果精确到个位)是( C )
(A)数据不全无法计算
(B)103
(C)104
(D)105
8.若一组数据1,2,3,4,x的平均数与中位数相同,则实数x的值不可能是( C )
A.0 B.2.5 C.3 D.5
9.若样本x1+1,x2+1,x3+1,……,xn+1的平均数为18,方差为2,则对于样本x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是(
)
A.平均数为18,方差为2
B.平均数为19,方差为3
C.平均数为19,方差为2
D.平均数为20,方差为4
10.某住宅小区六月份1日至5日每天用水量变化情况如图所示,那么这5天平均每天的用水量是(
C
)
A.30吨
B.31吨
C.32吨
D.33吨
3.下列各组数据中,组中值不是10的是(
D
)
A.0≤x<20
B.8≤x<12
C.7≤x<13
D.3≤x<7
填空题
11.滨城区李宁专卖店上个月销售的男运动鞋尺码统计如下:
码号(码)
38
39
40
41
42
43
44
销售量(双)
6
8
14
20
17
3
1
这组统计数据的众数是 40 码.?
12.某初中学校共有学生720人,该校有关部门从全体学生中随机抽取了50人对其到校方式进行调查,并将调查结果制成了如图所示的条形统计图,由此可以估计全校坐公交车到校的学生有_____7_____人.
13.一个样本为1,3,2,2,a,b,c.已知这个样本的众数为3,平均数为2,则这组数据的中位数为 2 .?
14.某学生在一次考试中,语文、数学、英语三门学科的平均成绩是80分,物理、化学两门学科的平均成绩为85分,则该学生这五门学科的平均成绩是 82 分.?
15.已知一组数据a,b,c的平均数为5,方差为4,那么数据a-2,b-2,c-2的平均数和方差分别是
答案3,4
16.某同学在体育训练中统计了自己五次“1分钟跳绳”的成绩,并绘制了如图所示的折线统计图,这五次“1分钟跳绳”成绩的中位数是 183 .?
三、解答题
17.某校为了解全校2
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
解:(1)=(0.5×15+1.0×20+1.5×10+2.0×5)=1.05(小时),
这50名学生在这一天平均每人的课外阅读所用时间是1.05小时.
(2)2
000×=1
400(人),
所以全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有1
400人.
18.某厂生产A,B两种产品,其单价随市场变化而进行相应的调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
并求得了A产品三次单价的平均数和方差:=5.9,=×[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=.
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;?
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
解析 (1)如图.
B产品第三次的单价比上一次的单价降低了25%.
(2)=×(3.5+4+3)=3.5,
=×[(3.5-3.5)2+(4-3.5)2+(3-3.5)2]=.
∵<,∴B产品的单价波动小.
(3)第四次调价后,对于A产品,这四次单价的中位数为=(元/件).
对于B产品,∵m>0,∴第四次单价大于3.
又∵×2-1=>,
∴第四次单价小于4(元/件),
∴×2-1=,∴m=25.
18.在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一
68
88
100
100
79
94
89
85
100
88
100
90
98
97
77
94
96
100
92
67
初二
69
97
91
69
98
100
99
100
90
100
99
69
97
100
99
94
79
99
98
79
(1)根据上述数据,将下列表格补充完整.
整理、描述数据:
分数段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
初一人数
2
2
4
12
初二人数
2
2
1
15
分析数据:样本数据的平均数、中位数、满分率如表:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
91.3
?
20%
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 (人);?
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
解:(1)由题意知初二年级的分数从小到大排列为69,69,69,79,
79,90,91,94,97,97,98,98,99,99,99,99,100,100,100,100,
所以初二年级成绩的中位数为97.5分,
补全表格如下:
年级
平均数
中位数
满分率
初一
90.1
93
25%
初二
91.3
97.5 ?
20%
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数为300×25%+300×20%=135(人).
(3)初二年级掌握禁毒知识的总体水平较好,
∵初二年级的平均成绩比初一高,说明初二年级平均水平高,且初二年级成绩的中位数比初一大,说明初二年级的得高分人数多于初一,
∴初二年级掌握禁毒知识的总体水平较好.
20.某校要从九年级(一)班和(二)班中各选取10名女同学组成礼仪队,选取的两班女生的身高如下:(单位:厘米)
(一)班:168
167
170
165
168
166
171
168
167
170
(二)班:165
167
169
170
165
168
170
171
168
167
(1)补充完成下面的统计分析表:
班级
平均数
方差
中位数
(一)班
168
168
(二)班
168
3.8
(2)请选一个合适的统计量作为选择标准,说明哪一个班能被选取.
解(1)3.2;168.
(2)选择方差作标准,
∵(一)班方差<(二)班方差,
∴(一)班能被选取.
21.学校广播站要招聘一名播音员,测试形象、知识面、普通话三个项目,按形象占10%,知识面占40%,普通话占50%计算加权平均数,作为最后评定的总成绩.
李文和孔明两位同学的各项成绩如表:
项目
选手
形象
知识面
普通话
李文
70
80
88
孔明
80
75
x
(1)计算李文同学的总成绩;
(2)若孔明同学要在总成绩上超过李文同学,则他的普通话成绩x应超过多少分?
解:(1)李文同学的总成绩为
70×10%+80×40%+88×50%=83(分).
(2)孔明同学的总成绩为80×10%+75×40%+50%·x.
根据题意,得80×10%+75×40%+50%·x>83,解得x>90.
答:若孔明同学要在总成绩上超过李文同学,则他的普通话成绩应超过90分.
