湘教版九年级数学下册 第2章 圆 单元测试(含答案)
文档属性
| 名称 | 湘教版九年级数学下册 第2章 圆 单元测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 330.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-04 19:41:37 | ||
图片预览



文档简介
第2章
圆
单元测试(2)
1、选择题
1.如图,在⊙O中,半径OC与弦AB垂直于点D,且AB=8,OC=5,则CD的长是( )
A.3
B.2.5
C.2
D.1
2.如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为3m和4m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( )
A.?2m?????B.?3m????C.?4m?????D.?6m
3.下列说法中正确的是(
)
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
4.如图,点?A,B,C均在6×6的正方形网格格点上,过A,B,C三点的圆除经过A,B,C三点外还能经过的格点最多有(?)个
A.
2
B.3
C.4
D.5
5.如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD=(???)
A.?32°??B.?42°????C.?58°??????D.?64°
6.如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于( )
A.??????B.2??????C.1??????D.
7.如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为( )
A.
B.
C.
D.
8.如图,点A、B、C是⊙O上的三点,若∠BOC=80°,则∠A的度数是(??
)
A.?40°???B.?60°????C.?80°????D.?100°
9.如图,AB是半圆的直径,AB=2r,C、D为半圆的三等分点,则图中阴影部分的面积是(??
).
A.?πr2???B.?πr2???C.?πr2????D.?πr2
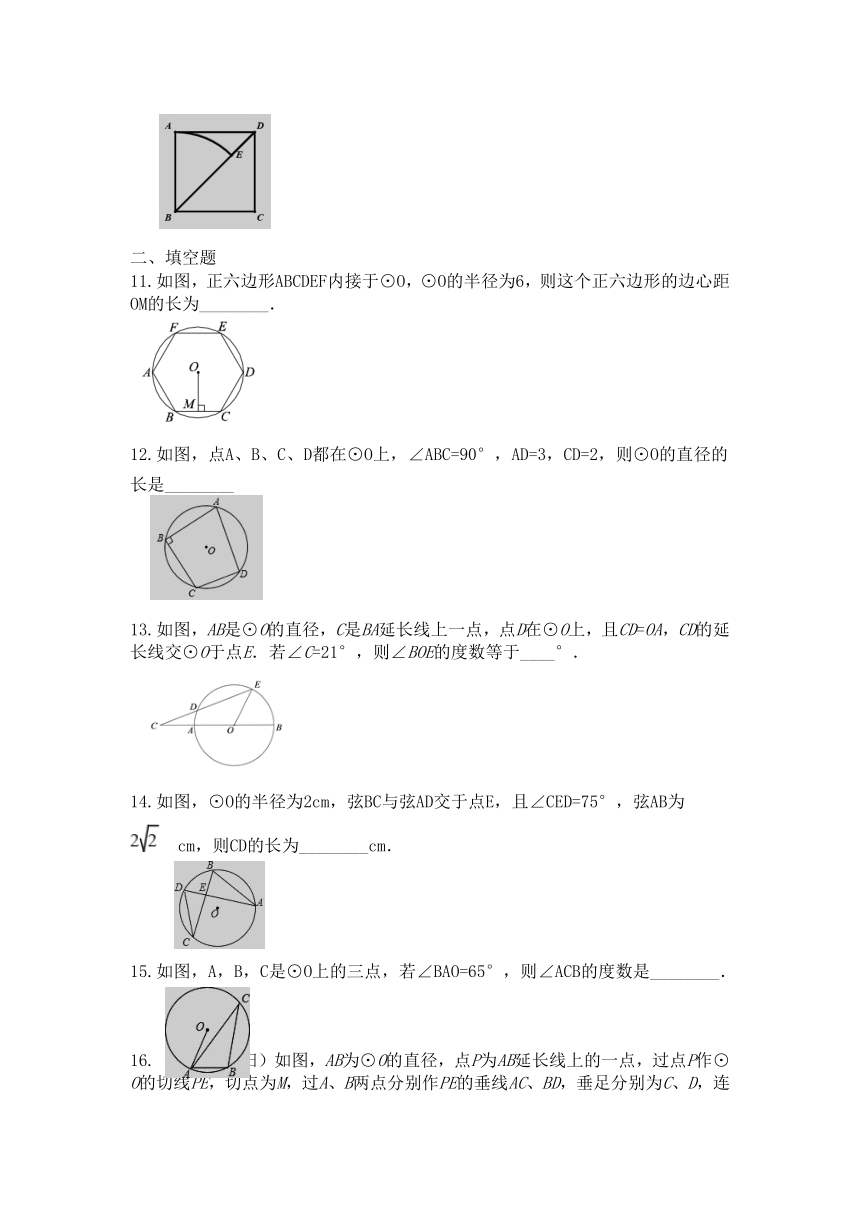
10.(2019·枣庄)如图,在边长为4的正方形ABCD中,以点B为圆心,AB为半径画弧,交对角线BD与点E,则图中阴影部分的面积是(结果保留)(
)
A.8-
B.16-2
C.8-2
D.8-
2、填空题
11.如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为________.
12.如图,点A、B、C、D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径的长是________?
13.如图,AB是⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E.若∠C=21°,则∠BOE的度数等于____°.
14.如图,⊙O的半径为2cm,弦BC与弦AD交于点E,且∠CED=75°,弦AB为
?cm,则CD的长为________cm.
15.如图,A,B,C是⊙O上的三点,若∠BAO=65°,则∠ACB的度数是________.
16.(2019·岳阳)如图,AB为⊙O的直径,点P为AB延长线上的一点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE的垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是_____.(写出所有正确结论的序号)
①AM平分∠CAB;②AM2=AC·AB;
③若AB=4,∠APE=30°,则的长为;
④若AC=3,BD=1,则有CM=DM=.
3、综合题
17.如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.
(1)若AC=4,BC=2,求OE的长;
(2)试判断∠A与∠CDE的数量关系,并说明理由.
18.
如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
(1)求证:AC是⊙O的切线;
(2)已知sin
A=,⊙O的半径为4,求图中阴影部分的面积.
19.(2019·广元)如图,AB是O的直径,点P是BA延长线上一点,过点P作O的切线PC,切点是C,过点C作弦CD⊥AB于E,连接CO,CB.
(1)求证:PD是O的切线;
(2)若AB=10,tanB=,求PA的长;
(3)试探究线段AB,OE,OP之间的数量关系,并说明理由.
第2章
圆
单元测试(2)答案
1、选择题
1.
C
2.B
3.B
4.D
5.A
6.C
7.B
8.A
9.B
10.C
二、填空题
11.3
12.
13.63
14.2
15.250
16.①②④
三、综合题
17.解:(1)∵AB是⊙O的直径,∴∠ACB=90°.
在Rt△ABC中,由勾股定理,得AB===2
,
∴AO=AB=×2
=.
∵OD⊥AB,
∴∠AOE=∠ACB=90°.
又∵∠A=∠A,
∴△AOE∽△ACB,
∴=,∴OE===.
(2)∠CDE=2∠A.理由如下:
如图所示,连接OC.
∵OA=OC,∴∠1=∠A.
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,∴∠2+∠CDE=90°.
∵OD⊥AB,∴∠2+∠3=90°.
∴∠3=∠CDE.
∵∠3=∠A+∠1=2∠A,∴∠CDE=2∠A.
18.解:(1)连接OE.
∵OB=OE
∴∠OBE=∠OEB
∵BE是△ABC的角平分线
∴∠OBE=∠EBC
∴∠OEB=∠EBC
∴OE∥BC
∵∠C=90°
∴∠AEO=∠C=90°
∴AC是圆O的切线;
(2)连接OF.
∵sinA=,∴∠A=30°?
∵圆O的半径为4,∴AO=2OE=8,
∴AE=4,∠AOE=60°,
∴AB=12,
∴BC=AB=6??
AC=6,
∴CE=AC﹣AE=2.
∵OB=OF,∠ABC=60°,
∴△OBF是正三角形.
∴∠FOB=60°,CF=6﹣4=2,?∠EOF=60°.
∴S梯形OECF=(2+4)×2=6?
S扇形EOF==
∴S阴影部分=S梯形OECF﹣S扇形EOF=6﹣.
19.
解:(1)连接OD,∵CD⊥AB,
∴CE=ED,
∴PC=PD,
∵OC=OD,
∴△POC≌△POD,
∴∠PDO=∠PCO,
∵PC是O的切线,
∴PC⊥OC,∠PCO=90°,
∴∠PDO=90°,
∴PD⊥DO,
∴PD是O的切线;
(2)
连接AC,∵tanB=,
∴设AC=x,则BC=2x,
∵AB=10,
∴AO=CO=5,在Rt△ABC中,由勾股定理可求得:AC=,BC=,
∴CE=4,EO=3,
∵△COE∽△POC,
∴PO=,
∴AP=PO-AO=;
(3)
∵△COE∽△POC,
∴,
∴CO2=PO·EO,
∵CO=,
∴=PO·EO,即AB2=4PO·EO.
圆
单元测试(2)
1、选择题
1.如图,在⊙O中,半径OC与弦AB垂直于点D,且AB=8,OC=5,则CD的长是( )
A.3
B.2.5
C.2
D.1
2.如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为3m和4m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( )
A.?2m?????B.?3m????C.?4m?????D.?6m
3.下列说法中正确的是(
)
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
4.如图,点?A,B,C均在6×6的正方形网格格点上,过A,B,C三点的圆除经过A,B,C三点外还能经过的格点最多有(?)个
A.
2
B.3
C.4
D.5
5.如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD=(???)
A.?32°??B.?42°????C.?58°??????D.?64°
6.如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于( )
A.??????B.2??????C.1??????D.
7.如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为( )
A.
B.
C.
D.
8.如图,点A、B、C是⊙O上的三点,若∠BOC=80°,则∠A的度数是(??
)
A.?40°???B.?60°????C.?80°????D.?100°
9.如图,AB是半圆的直径,AB=2r,C、D为半圆的三等分点,则图中阴影部分的面积是(??
).
A.?πr2???B.?πr2???C.?πr2????D.?πr2
10.(2019·枣庄)如图,在边长为4的正方形ABCD中,以点B为圆心,AB为半径画弧,交对角线BD与点E,则图中阴影部分的面积是(结果保留)(
)
A.8-
B.16-2
C.8-2
D.8-
2、填空题
11.如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为________.
12.如图,点A、B、C、D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径的长是________?
13.如图,AB是⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E.若∠C=21°,则∠BOE的度数等于____°.
14.如图,⊙O的半径为2cm,弦BC与弦AD交于点E,且∠CED=75°,弦AB为
?cm,则CD的长为________cm.
15.如图,A,B,C是⊙O上的三点,若∠BAO=65°,则∠ACB的度数是________.
16.(2019·岳阳)如图,AB为⊙O的直径,点P为AB延长线上的一点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE的垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是_____.(写出所有正确结论的序号)
①AM平分∠CAB;②AM2=AC·AB;
③若AB=4,∠APE=30°,则的长为;
④若AC=3,BD=1,则有CM=DM=.
3、综合题
17.如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.
(1)若AC=4,BC=2,求OE的长;
(2)试判断∠A与∠CDE的数量关系,并说明理由.
18.
如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
(1)求证:AC是⊙O的切线;
(2)已知sin
A=,⊙O的半径为4,求图中阴影部分的面积.
19.(2019·广元)如图,AB是O的直径,点P是BA延长线上一点,过点P作O的切线PC,切点是C,过点C作弦CD⊥AB于E,连接CO,CB.
(1)求证:PD是O的切线;
(2)若AB=10,tanB=,求PA的长;
(3)试探究线段AB,OE,OP之间的数量关系,并说明理由.
第2章
圆
单元测试(2)答案
1、选择题
1.
C
2.B
3.B
4.D
5.A
6.C
7.B
8.A
9.B
10.C
二、填空题
11.3
12.
13.63
14.2
15.250
16.①②④
三、综合题
17.解:(1)∵AB是⊙O的直径,∴∠ACB=90°.
在Rt△ABC中,由勾股定理,得AB===2
,
∴AO=AB=×2
=.
∵OD⊥AB,
∴∠AOE=∠ACB=90°.
又∵∠A=∠A,
∴△AOE∽△ACB,
∴=,∴OE===.
(2)∠CDE=2∠A.理由如下:
如图所示,连接OC.
∵OA=OC,∴∠1=∠A.
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,∴∠2+∠CDE=90°.
∵OD⊥AB,∴∠2+∠3=90°.
∴∠3=∠CDE.
∵∠3=∠A+∠1=2∠A,∴∠CDE=2∠A.
18.解:(1)连接OE.
∵OB=OE
∴∠OBE=∠OEB
∵BE是△ABC的角平分线
∴∠OBE=∠EBC
∴∠OEB=∠EBC
∴OE∥BC
∵∠C=90°
∴∠AEO=∠C=90°
∴AC是圆O的切线;
(2)连接OF.
∵sinA=,∴∠A=30°?
∵圆O的半径为4,∴AO=2OE=8,
∴AE=4,∠AOE=60°,
∴AB=12,
∴BC=AB=6??
AC=6,
∴CE=AC﹣AE=2.
∵OB=OF,∠ABC=60°,
∴△OBF是正三角形.
∴∠FOB=60°,CF=6﹣4=2,?∠EOF=60°.
∴S梯形OECF=(2+4)×2=6?
S扇形EOF==
∴S阴影部分=S梯形OECF﹣S扇形EOF=6﹣.
19.
解:(1)连接OD,∵CD⊥AB,
∴CE=ED,
∴PC=PD,
∵OC=OD,
∴△POC≌△POD,
∴∠PDO=∠PCO,
∵PC是O的切线,
∴PC⊥OC,∠PCO=90°,
∴∠PDO=90°,
∴PD⊥DO,
∴PD是O的切线;
(2)
连接AC,∵tanB=,
∴设AC=x,则BC=2x,
∵AB=10,
∴AO=CO=5,在Rt△ABC中,由勾股定理可求得:AC=,BC=,
∴CE=4,EO=3,
∵△COE∽△POC,
∴PO=,
∴AP=PO-AO=;
(3)
∵△COE∽△POC,
∴,
∴CO2=PO·EO,
∵CO=,
∴=PO·EO,即AB2=4PO·EO.
