湖南省长沙市长沙县第九中学2019-2020学年高二下学期学业水平模拟考试数学试卷 Word版含答案
文档属性
| 名称 | 湖南省长沙市长沙县第九中学2019-2020学年高二下学期学业水平模拟考试数学试卷 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 197.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-07 19:55:40 | ||
图片预览


文档简介
湖南省长沙市长沙县第九中学2019-2020学年高二下学期
学业水平模拟考试数学试卷
时量:90分钟
总分:100分
注意事项:
1.本试卷含三大题,19道小题,共4页.
2.答题前,考生务必将自己的姓名、准考证号填写在答题卡相应的位置.
3.全部答案在答题卡上完成,答在本试卷上无效.
一、选择题:本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.
已知集合
,,则
A.
B.
C.
D.
2.
下列判断不正确的是
A.;
B.;
C.;
D..
3.
下列几何体中,正视图、侧视图、俯视图都可以相同的几何体的序号是
A.
(1)
B.
(2)
C.
(3)
D.
无法确定
4.
已知,,则
的值等于
A.
B.
C.
D.
5.
若向量
,
满足
,
与
的夹角为
,则
等于
A.
B.
C.
D.
2
6.
某校选修足球课程的学生中,高二年级有30名,高一年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本,已知在高二年级的学生中抽取了6名,则在高一年级的学生中应抽取的人数为
A.6
B.8
C.10
D.12
7.
已知等比数列中,,公比,则等于
A.1
B.-1
C.2
D.
8.
对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如右图所示),则关于该样本的说法正确的是
A.
为8;
B.
为7;
C.
中位数是46;
D.
样本容量为31.
9.
在△ABC中,已知,则
A.
B.
C.
D.
10.
以点
为圆心,且与
轴相切的圆的标准方程为
A.
B.
C.
D.
2、填空题:本大题共5小题,每小题4分.
11.
已知等差数列
中,则
.
12.
函数的零点是
?.
13.
直线
的斜率为
?.
14.
不等式的解集是
.
15.
在△ABC中,如果,则角A等于
?.
三.解答题:本大题共4小题,共40分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分10分)
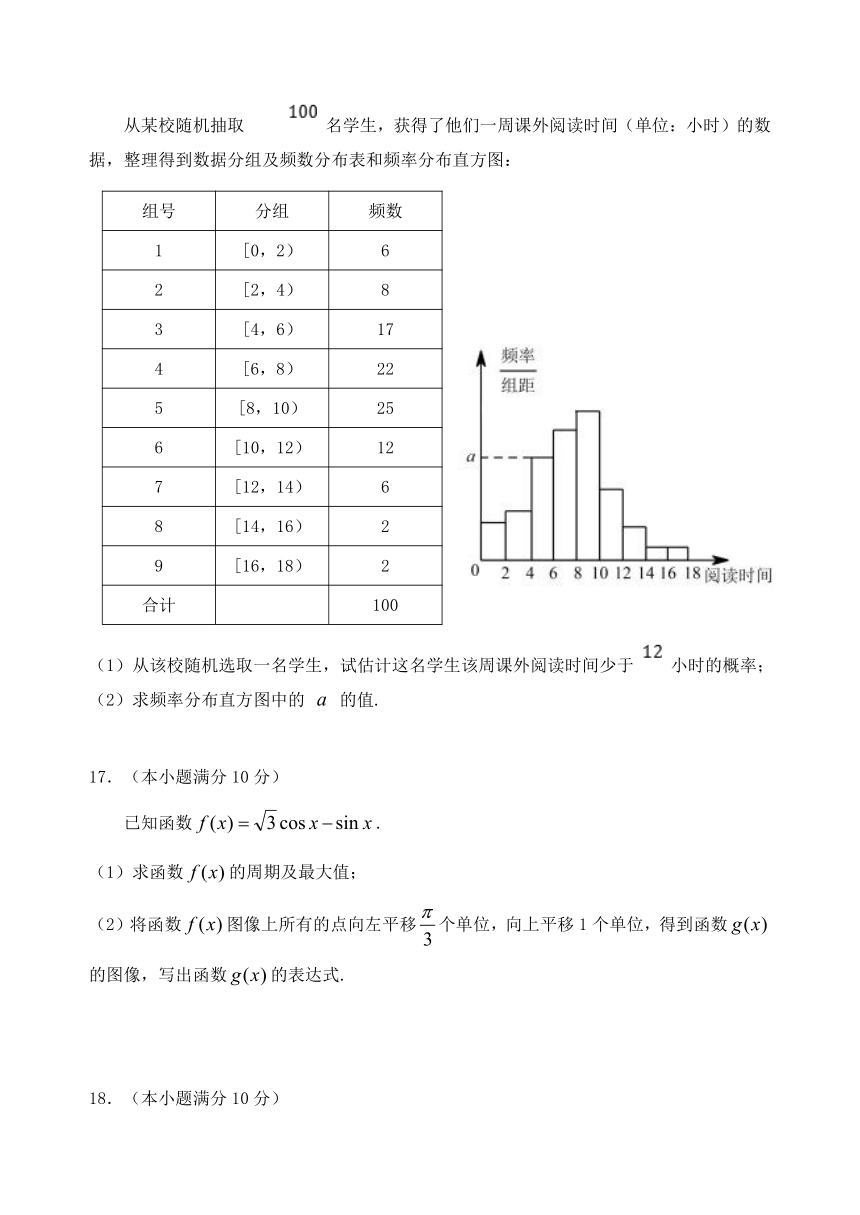
从某校随机抽取
名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
组号
分组
频数
1
[0,2)
6
2
[2,4)
8
3
[4,6)
17
4
[6,8)
22
5
[8,10)
25
6
[10,12)
12
7
[12,14)
6
8
[14,16)
2
9
[16,18)
2
合计
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于
小时的概率;
(2)求频率分布直方图中的
的值.
17.(本小题满分10分)
已知函数.
(1)求函数的周期及最大值;
(2)将函数图像上所有的点向左平移个单位,向上平移1个单位,得到函数的图像,写出函数的表达式.
18.(本小题满分10分)
如图,直三棱柱
的侧棱长为
,,,
是
的中点.
(1)求证:;
(2)求三棱锥
的体积.
19.(本小题满分10分)
已知函数
.
(1)写出函数的定义域及奇偶性;
(2)请判断函数在上的单调性,并用定义证明在上的单调性;
(3)当时,恒成立,求实数的取值范围.
数
学
参考答案
一、选择题:(每小题4分,共40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
B
A
B
C
C
C
A
二、填空题:(每小题4分,共20分)
11.80
12.2
13.
14.
或
15.
三、解答题:
(共40分)
16.(本小题满分10分)(1)
根据频数分布表,
名学生中课外阅读时间不少于
小时的学生共有
名,所以样本中的学生课外阅读时间少于
小时的频率是
从该校随机选取一名学生,估计这名学生该周课外阅读时间少于
小时的概率为
.…………6分
(2)
课外阅读时间落在组
的有
人,频率为
,所以
……………………………………………………………………10分
17.(本小题满分10分)(1)函数可化为……………………………………3分
周期为,……………………………………………………………………………………………4分
最大值为2.………………………………………………………………………………………………5分
(2)将函数图像上所有的点向左平移个单位,向上平移1个单位,
得到函数+1………………………………………………………………10分
18.(本小题满分10分)(1)
在
中,,
是
的中点,所以
,……2分
又因为
是直三棱柱,所以
,
因为,
所以
,………………4分
因为
,,
所以
.……………………………………5分
(2)
由()可知,,且
,……………………………6分
所以………………………………………………………………8分
………………………………………………………………10分
19.(本小题满分10分)(1)函数的定义域为,…………………………………2分
其为奇函数;
……………………………………………………3分
(2)在内单调递减.……………………………4分
下面证明:任取且
………6分
因为,所以,所以
因为,即.
因此,函数在上是单调减函数;…………………………………………………7分
(3)由得恒成立.……………………………………………8分
由(2)知,函数在为减函数.
…………………………………9分
当取得最小值
因此,实数的取值范围是.……………………………………………………………10分
(第三问也可分类讨论求出函数需酌情计分。)
学业水平模拟考试数学试卷
时量:90分钟
总分:100分
注意事项:
1.本试卷含三大题,19道小题,共4页.
2.答题前,考生务必将自己的姓名、准考证号填写在答题卡相应的位置.
3.全部答案在答题卡上完成,答在本试卷上无效.
一、选择题:本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.
已知集合
,,则
A.
B.
C.
D.
2.
下列判断不正确的是
A.;
B.;
C.;
D..
3.
下列几何体中,正视图、侧视图、俯视图都可以相同的几何体的序号是
A.
(1)
B.
(2)
C.
(3)
D.
无法确定
4.
已知,,则
的值等于
A.
B.
C.
D.
5.
若向量
,
满足
,
与
的夹角为
,则
等于
A.
B.
C.
D.
2
6.
某校选修足球课程的学生中,高二年级有30名,高一年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本,已知在高二年级的学生中抽取了6名,则在高一年级的学生中应抽取的人数为
A.6
B.8
C.10
D.12
7.
已知等比数列中,,公比,则等于
A.1
B.-1
C.2
D.
8.
对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如右图所示),则关于该样本的说法正确的是
A.
为8;
B.
为7;
C.
中位数是46;
D.
样本容量为31.
9.
在△ABC中,已知,则
A.
B.
C.
D.
10.
以点
为圆心,且与
轴相切的圆的标准方程为
A.
B.
C.
D.
2、填空题:本大题共5小题,每小题4分.
11.
已知等差数列
中,则
.
12.
函数的零点是
?.
13.
直线
的斜率为
?.
14.
不等式的解集是
.
15.
在△ABC中,如果,则角A等于
?.
三.解答题:本大题共4小题,共40分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分10分)
从某校随机抽取
名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
组号
分组
频数
1
[0,2)
6
2
[2,4)
8
3
[4,6)
17
4
[6,8)
22
5
[8,10)
25
6
[10,12)
12
7
[12,14)
6
8
[14,16)
2
9
[16,18)
2
合计
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于
小时的概率;
(2)求频率分布直方图中的
的值.
17.(本小题满分10分)
已知函数.
(1)求函数的周期及最大值;
(2)将函数图像上所有的点向左平移个单位,向上平移1个单位,得到函数的图像,写出函数的表达式.
18.(本小题满分10分)
如图,直三棱柱
的侧棱长为
,,,
是
的中点.
(1)求证:;
(2)求三棱锥
的体积.
19.(本小题满分10分)
已知函数
.
(1)写出函数的定义域及奇偶性;
(2)请判断函数在上的单调性,并用定义证明在上的单调性;
(3)当时,恒成立,求实数的取值范围.
数
学
参考答案
一、选择题:(每小题4分,共40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
B
A
B
C
C
C
A
二、填空题:(每小题4分,共20分)
11.80
12.2
13.
14.
或
15.
三、解答题:
(共40分)
16.(本小题满分10分)(1)
根据频数分布表,
名学生中课外阅读时间不少于
小时的学生共有
名,所以样本中的学生课外阅读时间少于
小时的频率是
从该校随机选取一名学生,估计这名学生该周课外阅读时间少于
小时的概率为
.…………6分
(2)
课外阅读时间落在组
的有
人,频率为
,所以
……………………………………………………………………10分
17.(本小题满分10分)(1)函数可化为……………………………………3分
周期为,……………………………………………………………………………………………4分
最大值为2.………………………………………………………………………………………………5分
(2)将函数图像上所有的点向左平移个单位,向上平移1个单位,
得到函数+1………………………………………………………………10分
18.(本小题满分10分)(1)
在
中,,
是
的中点,所以
,……2分
又因为
是直三棱柱,所以
,
因为,
所以
,………………4分
因为
,,
所以
.……………………………………5分
(2)
由()可知,,且
,……………………………6分
所以………………………………………………………………8分
………………………………………………………………10分
19.(本小题满分10分)(1)函数的定义域为,…………………………………2分
其为奇函数;
……………………………………………………3分
(2)在内单调递减.……………………………4分
下面证明:任取且
………6分
因为,所以,所以
因为,即.
因此,函数在上是单调减函数;…………………………………………………7分
(3)由得恒成立.……………………………………………8分
由(2)知,函数在为减函数.
…………………………………9分
当取得最小值
因此,实数的取值范围是.……………………………………………………………10分
(第三问也可分类讨论求出函数需酌情计分。)
同课章节目录
