3.1独立性检验-苏教版高中数学选修2-3课件(共22张PPT)
文档属性
| 名称 | 3.1独立性检验-苏教版高中数学选修2-3课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 540.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 14:07:53 | ||
图片预览




文档简介
(共22张PPT)
3.1
独
立
性
检
验
问题情景
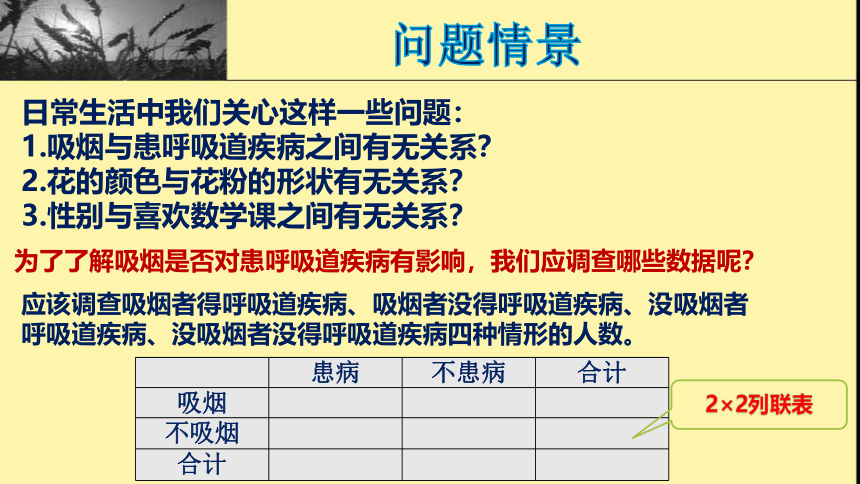
日常生活中我们关心这样一些问题:
1.吸烟与患呼吸道疾病之间有无关系?
2.花的颜色与花粉的形状有无关系?
3.性别与喜欢数学课之间有无关系?
为了了解吸烟是否对患呼吸道疾病有影响,我们应调查哪些数据呢?
应该调查吸烟者得呼吸道疾病、吸烟者没得呼吸道疾病、没吸烟者呼吸道疾病、没吸烟者没得呼吸道疾病四种情形的人数。
患病
不患病
合计
吸烟
不吸烟
合计
2×2列联表
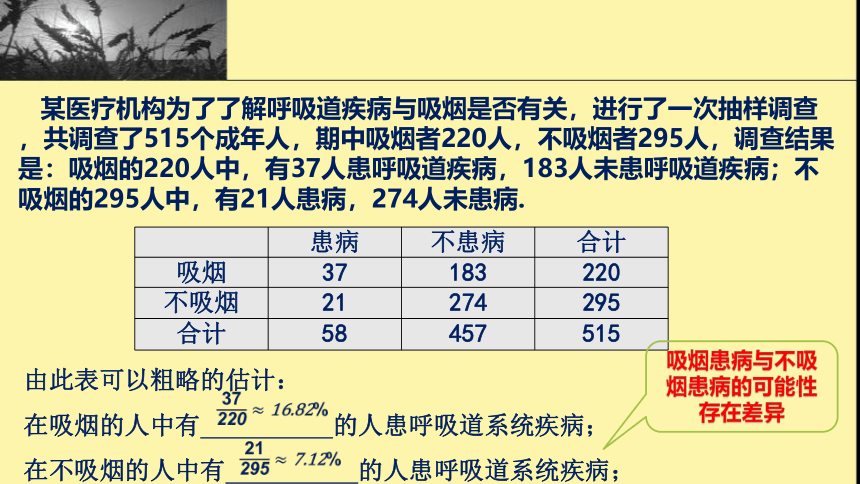
某医疗机构为了了解呼吸道疾病与吸烟是否有关,进行了一次抽样调查,共调查了515个成年人,期中吸烟者220人,不吸烟者295人,调查结果是:吸烟的220人中,有37人患呼吸道疾病,183人未患呼吸道疾病;不吸烟的295人中,有21人患病,274人未患病.
患病
不患病
合计
吸烟
37
183
220
不吸烟
21
274
295
合计
58
457
515
由此表可以粗略的估计:
在吸烟的人中有
的人患呼吸道系统疾病;
在不吸烟的人中有
的人患呼吸道系统疾病;
?
?
吸烟患病与不吸烟患病的可能性存在差异
问题1:判断的标准是什么?
问题2:差异大到什么程度才能作出“吸烟与患病有关”的判断?
问题3:能否用数量刻画出“有关”的程度?
在吸烟的人中有
的人患呼吸道系统疾病;
在不吸烟的人中有
的人患呼吸道系统疾病;
?
?
上面我们通过分析数据,得到的直观印象是吸烟和患呼吸道系统疾病有关,那么事实是否真的如此呢?能有多大的把握认为“吸烟与患病有关”?这需要用统计观点来考察这个问题。
上面我们通过分析数据,得到的直观印象是吸烟和患呼吸道系统疾病有关,那么事实是否真的如此呢?能有多大的把握认为“吸烟与患病有关”?这需要用统计观点来考察这个问题。
首先,给出假设:
H0
:患病与吸烟没有关系!
用A表示吸烟,B表示患病,则“吸烟与患病是否有关”等价于“吸烟与患病是否独立”,即假设H0等价于
P(AB)=P(A)P(B)是否成立.
问题1:P(A)、P(B)、P(AB)的值都未知怎么办?
答:用频率代替概率,估计P(A)、P(B)、P(AB)的值.
患病
未患病
总计
吸烟
a
b
a+b
不吸烟
c
d
c+d
总计
a+c
b+d
a+b+c+d
?
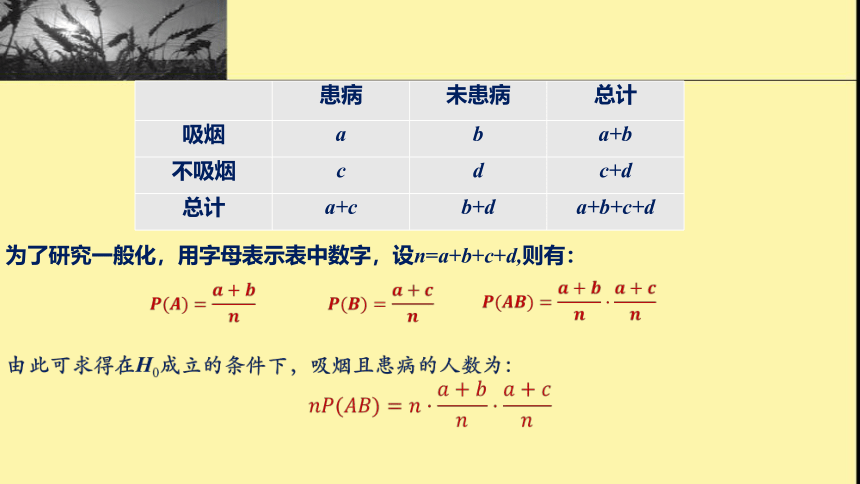
为了研究一般化,用字母表示表中数字,设n=a+b+c+d,则有:
?
?
?
患病
未患病
总计
吸烟
a
b
a+b
不吸烟
c
d
c+d
总计
a+c
b+d
a+b+c+d
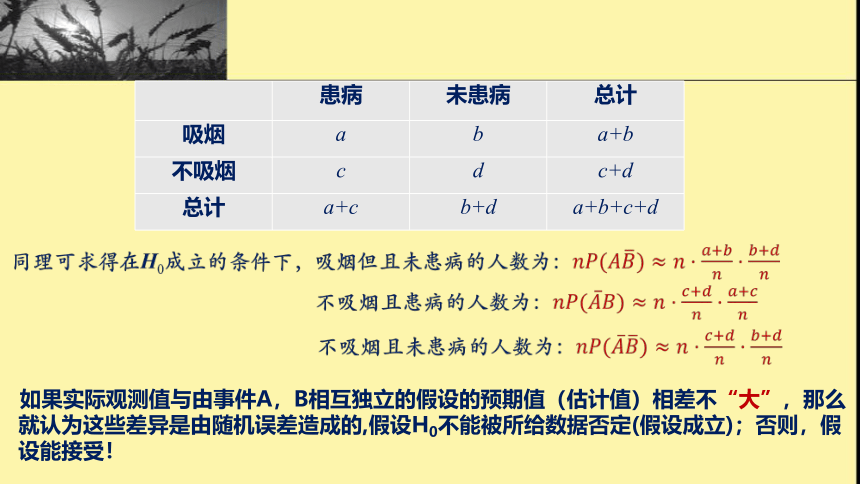
?
?
?
如果实际观测值与由事件A,B相互独立的假设的预期值(估计值)相差不“大”,那么就认为这些差异是由随机误差造成的,假设H0不能被所给数据否定(假设成立);否则,假设能接受!
问题:如何描述实际观测值与预期值(估计值)的差异?
?
?
问题情景
患病
不患病
合计
吸烟
37
183
220
不吸烟
21
274
295
合计
58
457
515
?
?
?
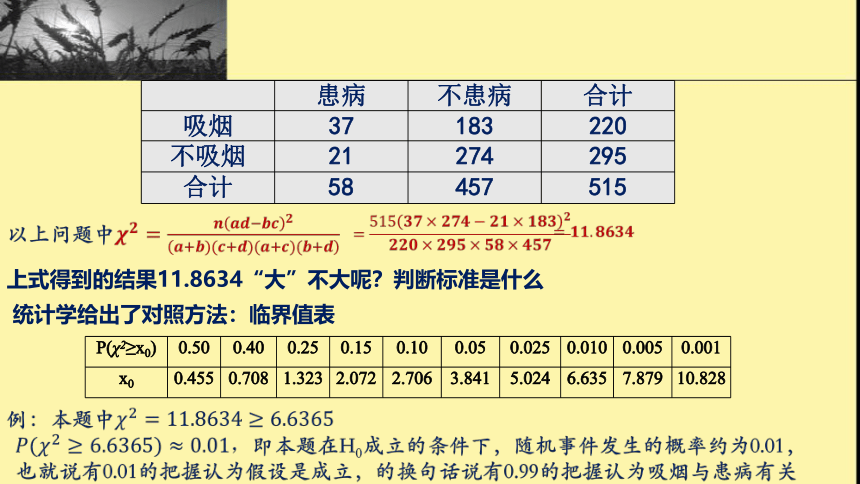
上式得到的结果11.8634“大”不大呢?判断标准是什么
P(χ2≥x0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
统计学给出了对照方法:临界值表
?
?
独立性检验:
用χ2统计量来研究两类因子彼此相关或相互独立的一种检验方法.
推断两个研究对象Ⅰ和Ⅱ是否相关的独立性检验步骤:
(1):提出假设H0:Ⅰ和Ⅱ没有关系;
(2):根据2×2列联表和χ2公式计算χ2的值.
(3):查对临界值表,给出结论.
Ⅱ
类1
类2
合计
Ⅰ
类A
a
b
a+b
类B
c
d
c+d
合计
a+c
b+d
a+b+c+d
基本概念
0.1%把握认为A与B无关
99.9%把握认为A与B有关
1%把握认为A与B无关
99%把握认为A与B有关
10%把握认为A与B无关
90%把握认为A与B有关
没有充分的依据显示A与B有关,但也不能显示A与B无关
P(χ2≥x0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
临界值表:
独立性检验:
用χ2统计量来研究两类因子彼此相关或相互独立的一种检验方法.
注
(1):如果算出的“χ2”值较大,就拒绝H0(统计假设),
即“事件A与B有关”。
(2):使用“χ2”统计量进行独立检验时,统计学要求表中的4个数据都要大于5,在选取样本时要注意这一点。
(3):在解决实际问题时,可以直接计算χ2的观测值k进行独立检验,而不必写出χ2的推导过程;
基本概念
1.对两类变量X与Y的统计量χ2=k,说法正确的是( )
A.k越大,“
X与Y有关系”可信程度越小
B.k越小,“
X与Y有关系”可信程度越小
C.k越接近于0,“X与Y无关”程度越小
D.k越大,“X与Y无关”程度越大
B
课堂练习
A
课堂练习
P(χ2≥x0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
例1.在500人身上试验某种血清预防感冒作用,把他们一年中的感冒记录与另外500名未用血清的人的感冒记录作比较,结果如表所示。问:该种血清能否起到预防感冒的作用?
未感冒
感冒
合计
使用血清
258
242
500
未使用血清
216
284
500
合计
474
526
1000
解:设H0:感冒与是否使用该血清没有关系.
因当H0成立时,χ2≥6.635的概率约为0.01,故有99%的把握认为该血清能起到预防感冒的作用.
典型例题
例2:为研究不同的给药方式(口服与注射)和药的效果(有效与无效)是否有关,进行了相应的抽样调查,调查的结果列在表中,根据所选择的193个病人的数据,能否作出药的效果和给药方式有关的结论?
有效
无效
合计
口服
58
40
98
注射
64
31
95
合计
122
71
193
解:设H0:药的效果与给药方式没有关系.
因当H0成立时,χ2≥1.3896的概率大于15%,故不能否定假设H0,即不能作出药的效果与给药方式有关的结论.
<2.072
典型例题
练习.打鼾不仅影响别人休息,而且可能与患某种疾病有关。下表是一次调查所得数据,试问:每一晚都打鼾与患心脏病有关吗?
患心脏病
未患心脏病
合计
每晚打鼾
30
224
254
不打鼾
24
1355
1379
合计
54
1579
1633
课堂练习
例3:气管炎是一种常见的呼吸道疾病,医药研究人员对两种中草药治疗慢性气管炎的疗效进行对比,所得数据如表所示,问:它们的疗效有无差异?
有效
无效
合计
复方江剪刀草
184
61
245
胆黄片
91
9
100
合计
275
70
345
解:设H0:两种中草药的治疗效果没有差异。
因当H0成立时,χ2≥10.828的概率为0.001,故有99.9%的把握认为,两种药物的疗效有差异。
典型例题
典型例题
练习:某中学对高三甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
现规定平均成绩在80分以上(不含80分)的为优秀.
(1)试分别估计两个班级的优秀率;
(2)由以上统计数据填写列联表,并问是否有
75%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助?
解:(1)由题意知,甲乙两班学生均有50人
甲班优秀人数为30人,优秀率为
乙班优秀人数为25人,优秀率为
30
25
55
25
20
45
100
50
50
所以由参考数据知,没有75%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助.
3.1
独
立
性
检
验
问题情景
日常生活中我们关心这样一些问题:
1.吸烟与患呼吸道疾病之间有无关系?
2.花的颜色与花粉的形状有无关系?
3.性别与喜欢数学课之间有无关系?
为了了解吸烟是否对患呼吸道疾病有影响,我们应调查哪些数据呢?
应该调查吸烟者得呼吸道疾病、吸烟者没得呼吸道疾病、没吸烟者呼吸道疾病、没吸烟者没得呼吸道疾病四种情形的人数。
患病
不患病
合计
吸烟
不吸烟
合计
2×2列联表
某医疗机构为了了解呼吸道疾病与吸烟是否有关,进行了一次抽样调查,共调查了515个成年人,期中吸烟者220人,不吸烟者295人,调查结果是:吸烟的220人中,有37人患呼吸道疾病,183人未患呼吸道疾病;不吸烟的295人中,有21人患病,274人未患病.
患病
不患病
合计
吸烟
37
183
220
不吸烟
21
274
295
合计
58
457
515
由此表可以粗略的估计:
在吸烟的人中有
的人患呼吸道系统疾病;
在不吸烟的人中有
的人患呼吸道系统疾病;
?
?
吸烟患病与不吸烟患病的可能性存在差异
问题1:判断的标准是什么?
问题2:差异大到什么程度才能作出“吸烟与患病有关”的判断?
问题3:能否用数量刻画出“有关”的程度?
在吸烟的人中有
的人患呼吸道系统疾病;
在不吸烟的人中有
的人患呼吸道系统疾病;
?
?
上面我们通过分析数据,得到的直观印象是吸烟和患呼吸道系统疾病有关,那么事实是否真的如此呢?能有多大的把握认为“吸烟与患病有关”?这需要用统计观点来考察这个问题。
上面我们通过分析数据,得到的直观印象是吸烟和患呼吸道系统疾病有关,那么事实是否真的如此呢?能有多大的把握认为“吸烟与患病有关”?这需要用统计观点来考察这个问题。
首先,给出假设:
H0
:患病与吸烟没有关系!
用A表示吸烟,B表示患病,则“吸烟与患病是否有关”等价于“吸烟与患病是否独立”,即假设H0等价于
P(AB)=P(A)P(B)是否成立.
问题1:P(A)、P(B)、P(AB)的值都未知怎么办?
答:用频率代替概率,估计P(A)、P(B)、P(AB)的值.
患病
未患病
总计
吸烟
a
b
a+b
不吸烟
c
d
c+d
总计
a+c
b+d
a+b+c+d
?
为了研究一般化,用字母表示表中数字,设n=a+b+c+d,则有:
?
?
?
患病
未患病
总计
吸烟
a
b
a+b
不吸烟
c
d
c+d
总计
a+c
b+d
a+b+c+d
?
?
?
如果实际观测值与由事件A,B相互独立的假设的预期值(估计值)相差不“大”,那么就认为这些差异是由随机误差造成的,假设H0不能被所给数据否定(假设成立);否则,假设能接受!
问题:如何描述实际观测值与预期值(估计值)的差异?
?
?
问题情景
患病
不患病
合计
吸烟
37
183
220
不吸烟
21
274
295
合计
58
457
515
?
?
?
上式得到的结果11.8634“大”不大呢?判断标准是什么
P(χ2≥x0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
统计学给出了对照方法:临界值表
?
?
独立性检验:
用χ2统计量来研究两类因子彼此相关或相互独立的一种检验方法.
推断两个研究对象Ⅰ和Ⅱ是否相关的独立性检验步骤:
(1):提出假设H0:Ⅰ和Ⅱ没有关系;
(2):根据2×2列联表和χ2公式计算χ2的值.
(3):查对临界值表,给出结论.
Ⅱ
类1
类2
合计
Ⅰ
类A
a
b
a+b
类B
c
d
c+d
合计
a+c
b+d
a+b+c+d
基本概念
0.1%把握认为A与B无关
99.9%把握认为A与B有关
1%把握认为A与B无关
99%把握认为A与B有关
10%把握认为A与B无关
90%把握认为A与B有关
没有充分的依据显示A与B有关,但也不能显示A与B无关
P(χ2≥x0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
临界值表:
独立性检验:
用χ2统计量来研究两类因子彼此相关或相互独立的一种检验方法.
注
(1):如果算出的“χ2”值较大,就拒绝H0(统计假设),
即“事件A与B有关”。
(2):使用“χ2”统计量进行独立检验时,统计学要求表中的4个数据都要大于5,在选取样本时要注意这一点。
(3):在解决实际问题时,可以直接计算χ2的观测值k进行独立检验,而不必写出χ2的推导过程;
基本概念
1.对两类变量X与Y的统计量χ2=k,说法正确的是( )
A.k越大,“
X与Y有关系”可信程度越小
B.k越小,“
X与Y有关系”可信程度越小
C.k越接近于0,“X与Y无关”程度越小
D.k越大,“X与Y无关”程度越大
B
课堂练习
A
课堂练习
P(χ2≥x0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
例1.在500人身上试验某种血清预防感冒作用,把他们一年中的感冒记录与另外500名未用血清的人的感冒记录作比较,结果如表所示。问:该种血清能否起到预防感冒的作用?
未感冒
感冒
合计
使用血清
258
242
500
未使用血清
216
284
500
合计
474
526
1000
解:设H0:感冒与是否使用该血清没有关系.
因当H0成立时,χ2≥6.635的概率约为0.01,故有99%的把握认为该血清能起到预防感冒的作用.
典型例题
例2:为研究不同的给药方式(口服与注射)和药的效果(有效与无效)是否有关,进行了相应的抽样调查,调查的结果列在表中,根据所选择的193个病人的数据,能否作出药的效果和给药方式有关的结论?
有效
无效
合计
口服
58
40
98
注射
64
31
95
合计
122
71
193
解:设H0:药的效果与给药方式没有关系.
因当H0成立时,χ2≥1.3896的概率大于15%,故不能否定假设H0,即不能作出药的效果与给药方式有关的结论.
<2.072
典型例题
练习.打鼾不仅影响别人休息,而且可能与患某种疾病有关。下表是一次调查所得数据,试问:每一晚都打鼾与患心脏病有关吗?
患心脏病
未患心脏病
合计
每晚打鼾
30
224
254
不打鼾
24
1355
1379
合计
54
1579
1633
课堂练习
例3:气管炎是一种常见的呼吸道疾病,医药研究人员对两种中草药治疗慢性气管炎的疗效进行对比,所得数据如表所示,问:它们的疗效有无差异?
有效
无效
合计
复方江剪刀草
184
61
245
胆黄片
91
9
100
合计
275
70
345
解:设H0:两种中草药的治疗效果没有差异。
因当H0成立时,χ2≥10.828的概率为0.001,故有99.9%的把握认为,两种药物的疗效有差异。
典型例题
典型例题
练习:某中学对高三甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
现规定平均成绩在80分以上(不含80分)的为优秀.
(1)试分别估计两个班级的优秀率;
(2)由以上统计数据填写列联表,并问是否有
75%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助?
解:(1)由题意知,甲乙两班学生均有50人
甲班优秀人数为30人,优秀率为
乙班优秀人数为25人,优秀率为
30
25
55
25
20
45
100
50
50
所以由参考数据知,没有75%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助.
