3.2.1古典概型-人教A版高中数学必修三课件(共19张PPT)
文档属性
| 名称 | 3.2.1古典概型-人教A版高中数学必修三课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 587.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 14:03:38 | ||
图片预览






文档简介
(共19张PPT)
必修三
3.2.1
古典概型
回忆
你还记得概率的意义么?
在进行大量的重复实验后,事件A发生的频率会稳定在某个常数P附近,则常数P称为事件A发生的概率
——贝努利《大数定律》
考察实验
试验1:掷一枚质地均匀的硬币的试验;有哪些试验结果?
试验2:掷一枚质地均匀的骰子的试验;有哪些试验结果?
{出现1点},{出现2点},{出现3点}
{出现4点},{出现5点},{出现6点}
{正面朝上},{反面朝上}
基本事件定义
试验1:掷一枚质地均匀的硬币的试验;全部试验结果为
试验2:掷一枚质地均匀的骰子的试验;全部试验结果为
{出现1点},{出现2点},{出现3点}
{出现4点},{出现5点},{出现6点}
{正面朝上},{反面朝上}
试验中可能出现的每一个结果都称为一个基本事件
基本事件特点
问题1:任意两个基本事件之间是什么关系?
任何两个基本事件是互斥的
试验2:掷一枚质地均匀的骰子的试验,基本事件为
{出现1点},{出现2点},{出现3点}
{出现4点},{出现5点},{出现6点}
问题2:若事件A
={出现的点数为偶数},
事件B
={出现的点数不大于3}
则A,B可以用基本事件来表示吗?
A
={出现2点}+{出现4点}+{出现6点}
B
={出现1点}+{出现2点}+{出现3点}
任何事件(除不可能事件)都可以表示成基本事件的和
例一:
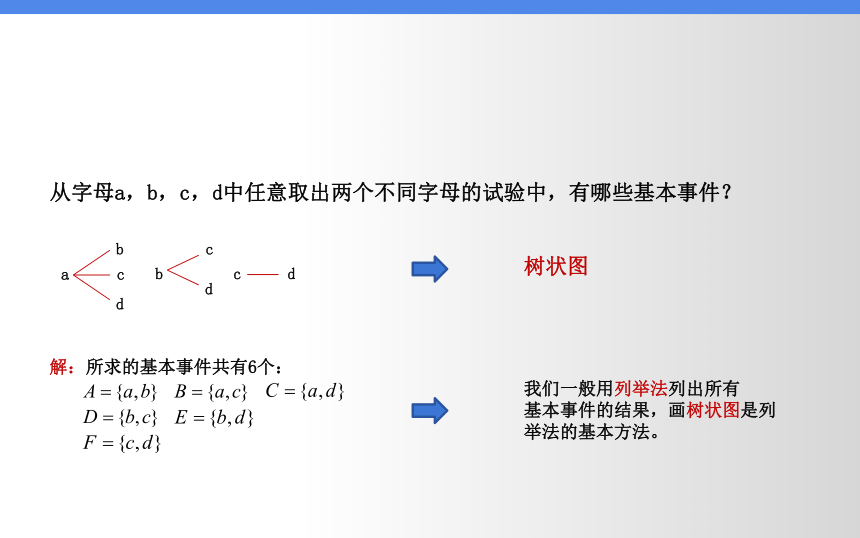
从字母a,b,c,d中任意取出两个不同字母的试验中,有哪些基本事件?
a
b
c
d
b
c
d
c
d
解:所求的基本事件共有6个:
树状图
我们一般用列举法列出所有
基本事件的结果,画树状图是列
举法的基本方法。
古典概型定义
“A”、“B”、“C”
“D”、“E”、“F”
例题1
“1点”、“2点”
“3点”、“4点”
“5点”、“6点”
试验二
“正面朝上”
“反面朝上”
试验一
相
同
不
同
(2)每个基本事件出现的可能性相等。
(等可能性)
我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型。
(1)试验中所有可能出现的基本事件只有有限个;
(有限性)
(有限性)
(等可能性)
判断
(1)向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么?
(2)如图,某同学随机地向靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环。你认为这是古典概型吗?为什么?
因为试验的所有可能结果是圆面内所有的点,试验的所有可能结果数是无限的,虽然每一个试验结果出现的“可能性相同”,但这个试验不满足古典概型的第一个条件。
不是古典概型,因为试验的所有可能结果只有7个,而命中10环、命中9环……命中5环和不中环的出现不是等可能的,即不满足古典概型的第二个条件。
公式推导
在古典概型下,基本事件出现的概率是多少?随机事件出现的概率如何计算?
(试验一
“正面朝上”的概率)
试验一掷硬币中,出现正面朝上的概率与反面朝上的概率相等,即
P(“正面朝上”)=
P(“反面朝上”)
由概率的加法公式,得
P(“正面朝上”)+P(“反面朝上”)=P(必然事件)=1
因此
P(“正面朝上”)=P(“反面朝上”)=
即
试验二掷骰子中,出现各个点的概率相等,即
P(“1点”)=P(“2点”)=P(“3点”)=P(“4点”)=P(“5点”)=P(“6点”)
反复利用概率的加法公式
P(“1点”)+P(“2点”)+P(“3点”)+P(“4点”)+P(“5点”)+P(“6点”)=P(必然事件)=1
所以P(“1点”)=P(“2点”)=P(“3点”)=P(“4点”)=P(“5点”)=P(“6点”)=
在古典概型下,基本事件出现的概率是多少?随机事件出现的概率如何计算?
(试验二
“出现1点”的概率
“出现偶数点”的概率)
P(“出现偶数点”)=P(“2点”)+P(“4点”)+P(“6点”)
=
+
+
=
即
概率公式
根据上述两个模拟试验,可以概括总结出,古典概型计算任何事件的概率计算公式为:
(1)在例1的实验中,出现字母“d”的概率是多少?
提问:
基本事件的个数为6,“出现字母d”所包含的基本事件个数为3,所以
(2)在使用古典概型的概率公式时,应该注意什么?
(1)要判断该概率模型是不是古典概型;
(2)要找出随机事件A包含的基本事件的个数和试验中基本事件的总数。
例二
例2
单选题是标准化考试中常用的题型,一般是从A,B,C,D四个选项中选择一个正确答案。如果考生掌握了考察的内容,他可以选择唯一正确的答案。假设考生不会做,他随机的选择一个答案,问他答对的概率是多少?
解:这是一个古典概型,基本事件为“选择A”、“选择B”、“选择C”、“选择D”,共有4个,
考生随机地选择一个答案是选择A,B,C,D的可能性是相等的。
由古典概型的概率计算公式得:
变式(1):在标准化考试中既有单选题又有多选题,多选题是从A,B,C,D四个选项中选出所有正确的答案,同学们可能有一种感觉,如果不知道正确答案,多选题更难猜对,这是为什么?
选对的概率又是多少呢?
例三
同时掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少?
解法一
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
(4,1)
(3,2)
(2,3)
(1,4)
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子
2号骰子
解:(1)掷一个骰子的结果有6种,我们把两个骰子标上记号1,2以便区分,我们用一个“有序实数对”来表示组成同时掷两个骰子的一个结果(如表),第一个数表示1号骰子,第二个数表示2号骰子。
从表中可以看出同时掷两个骰子的结果共有36种。
(2)在上面的结果中,向上的点数之和为5的结果有4种,分别为:(1,4),(2,3),(3,2),(4,1)
(3)由于所有36种结果是等可能的,其中向上点数之和为5的结果(记为事件A)有4种,因此,由古典概型的概率计算公式可得
列表法
解法二
(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)(2,2)(2,3)(2,4)(2,5)(2,6)(3,3)(3,4)(3,5)(3,6)(4,4)(4,5)(4,6)(5,5)(5,6)(6,6)
共有21种,和是5的结果有2个,它们是(1,4)(2,3),所求的概率为
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
(4,1)
(3,2)
(2,3)
(1,4)
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子
2号骰子
错
总结
1.古典概型:
我们将具有:
(1)试验中所有可能出现的基本事件只有有限个;(有限性)
(2)每个基本事件出现的可能性相等。(等可能性)
这样两个特点的概率模型称为古典概率概型,简称古典概型。
2.古典概型计算任何事件的概率计算公式为:
3.求某个随机事件A包含的基本事件的个数和实验中基本事件的总数常用的方法是列举法(画树状图和列表),注意做到不重不漏。
练习
某单位要在甲、乙、丙、丁四人中选两人分别担任周六、周日的值班任务(每人被安排是等可能的,每天只安排一人).
(Ⅰ)共有多少种安排方法?
(Ⅱ)其中甲、乙两人都被安排的概率是多少?
(Ⅲ)甲、乙两人中至少有一人被安排的概率是多少?
从1,2,
3,4,
5五个数字中,任取两数,求两数都是奇数的概率。至少一个奇数呢?
作业
P123
练习1、2
题
必修三
3.2.1
古典概型
回忆
你还记得概率的意义么?
在进行大量的重复实验后,事件A发生的频率会稳定在某个常数P附近,则常数P称为事件A发生的概率
——贝努利《大数定律》
考察实验
试验1:掷一枚质地均匀的硬币的试验;有哪些试验结果?
试验2:掷一枚质地均匀的骰子的试验;有哪些试验结果?
{出现1点},{出现2点},{出现3点}
{出现4点},{出现5点},{出现6点}
{正面朝上},{反面朝上}
基本事件定义
试验1:掷一枚质地均匀的硬币的试验;全部试验结果为
试验2:掷一枚质地均匀的骰子的试验;全部试验结果为
{出现1点},{出现2点},{出现3点}
{出现4点},{出现5点},{出现6点}
{正面朝上},{反面朝上}
试验中可能出现的每一个结果都称为一个基本事件
基本事件特点
问题1:任意两个基本事件之间是什么关系?
任何两个基本事件是互斥的
试验2:掷一枚质地均匀的骰子的试验,基本事件为
{出现1点},{出现2点},{出现3点}
{出现4点},{出现5点},{出现6点}
问题2:若事件A
={出现的点数为偶数},
事件B
={出现的点数不大于3}
则A,B可以用基本事件来表示吗?
A
={出现2点}+{出现4点}+{出现6点}
B
={出现1点}+{出现2点}+{出现3点}
任何事件(除不可能事件)都可以表示成基本事件的和
例一:
从字母a,b,c,d中任意取出两个不同字母的试验中,有哪些基本事件?
a
b
c
d
b
c
d
c
d
解:所求的基本事件共有6个:
树状图
我们一般用列举法列出所有
基本事件的结果,画树状图是列
举法的基本方法。
古典概型定义
“A”、“B”、“C”
“D”、“E”、“F”
例题1
“1点”、“2点”
“3点”、“4点”
“5点”、“6点”
试验二
“正面朝上”
“反面朝上”
试验一
相
同
不
同
(2)每个基本事件出现的可能性相等。
(等可能性)
我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型。
(1)试验中所有可能出现的基本事件只有有限个;
(有限性)
(有限性)
(等可能性)
判断
(1)向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么?
(2)如图,某同学随机地向靶心进行射击,这一试验的结果只有有限个:命中10环、命中9环……命中5环和不中环。你认为这是古典概型吗?为什么?
因为试验的所有可能结果是圆面内所有的点,试验的所有可能结果数是无限的,虽然每一个试验结果出现的“可能性相同”,但这个试验不满足古典概型的第一个条件。
不是古典概型,因为试验的所有可能结果只有7个,而命中10环、命中9环……命中5环和不中环的出现不是等可能的,即不满足古典概型的第二个条件。
公式推导
在古典概型下,基本事件出现的概率是多少?随机事件出现的概率如何计算?
(试验一
“正面朝上”的概率)
试验一掷硬币中,出现正面朝上的概率与反面朝上的概率相等,即
P(“正面朝上”)=
P(“反面朝上”)
由概率的加法公式,得
P(“正面朝上”)+P(“反面朝上”)=P(必然事件)=1
因此
P(“正面朝上”)=P(“反面朝上”)=
即
试验二掷骰子中,出现各个点的概率相等,即
P(“1点”)=P(“2点”)=P(“3点”)=P(“4点”)=P(“5点”)=P(“6点”)
反复利用概率的加法公式
P(“1点”)+P(“2点”)+P(“3点”)+P(“4点”)+P(“5点”)+P(“6点”)=P(必然事件)=1
所以P(“1点”)=P(“2点”)=P(“3点”)=P(“4点”)=P(“5点”)=P(“6点”)=
在古典概型下,基本事件出现的概率是多少?随机事件出现的概率如何计算?
(试验二
“出现1点”的概率
“出现偶数点”的概率)
P(“出现偶数点”)=P(“2点”)+P(“4点”)+P(“6点”)
=
+
+
=
即
概率公式
根据上述两个模拟试验,可以概括总结出,古典概型计算任何事件的概率计算公式为:
(1)在例1的实验中,出现字母“d”的概率是多少?
提问:
基本事件的个数为6,“出现字母d”所包含的基本事件个数为3,所以
(2)在使用古典概型的概率公式时,应该注意什么?
(1)要判断该概率模型是不是古典概型;
(2)要找出随机事件A包含的基本事件的个数和试验中基本事件的总数。
例二
例2
单选题是标准化考试中常用的题型,一般是从A,B,C,D四个选项中选择一个正确答案。如果考生掌握了考察的内容,他可以选择唯一正确的答案。假设考生不会做,他随机的选择一个答案,问他答对的概率是多少?
解:这是一个古典概型,基本事件为“选择A”、“选择B”、“选择C”、“选择D”,共有4个,
考生随机地选择一个答案是选择A,B,C,D的可能性是相等的。
由古典概型的概率计算公式得:
变式(1):在标准化考试中既有单选题又有多选题,多选题是从A,B,C,D四个选项中选出所有正确的答案,同学们可能有一种感觉,如果不知道正确答案,多选题更难猜对,这是为什么?
选对的概率又是多少呢?
例三
同时掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少?
解法一
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
(4,1)
(3,2)
(2,3)
(1,4)
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子
2号骰子
解:(1)掷一个骰子的结果有6种,我们把两个骰子标上记号1,2以便区分,我们用一个“有序实数对”来表示组成同时掷两个骰子的一个结果(如表),第一个数表示1号骰子,第二个数表示2号骰子。
从表中可以看出同时掷两个骰子的结果共有36种。
(2)在上面的结果中,向上的点数之和为5的结果有4种,分别为:(1,4),(2,3),(3,2),(4,1)
(3)由于所有36种结果是等可能的,其中向上点数之和为5的结果(记为事件A)有4种,因此,由古典概型的概率计算公式可得
列表法
解法二
(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)(2,2)(2,3)(2,4)(2,5)(2,6)(3,3)(3,4)(3,5)(3,6)(4,4)(4,5)(4,6)(5,5)(5,6)(6,6)
共有21种,和是5的结果有2个,它们是(1,4)(2,3),所求的概率为
(6,6)
(6,5)
(6,4)
(6,3)
(6,2)
(6,1)
(5,6)
(5,5)
(5,4)
(5,3)
(5,2)
(5,1)
(4,6)
(4,5)
(4,4)
(4,3)
(4,2)
(4,1)
(3,6)
(3,5)
(3,4)
(3,3)
(3,2)
(3,1)
(2,6)
(2,5)
(2,4)
(2,3)
(2,2)
(2,1)
(1,6)
(1,5)
(1,4)
(1,3)
(1,2)
(1,1)
(4,1)
(3,2)
(2,3)
(1,4)
6
5
4
3
2
1
6
5
4
3
2
1
1号骰子
2号骰子
错
总结
1.古典概型:
我们将具有:
(1)试验中所有可能出现的基本事件只有有限个;(有限性)
(2)每个基本事件出现的可能性相等。(等可能性)
这样两个特点的概率模型称为古典概率概型,简称古典概型。
2.古典概型计算任何事件的概率计算公式为:
3.求某个随机事件A包含的基本事件的个数和实验中基本事件的总数常用的方法是列举法(画树状图和列表),注意做到不重不漏。
练习
某单位要在甲、乙、丙、丁四人中选两人分别担任周六、周日的值班任务(每人被安排是等可能的,每天只安排一人).
(Ⅰ)共有多少种安排方法?
(Ⅱ)其中甲、乙两人都被安排的概率是多少?
(Ⅲ)甲、乙两人中至少有一人被安排的概率是多少?
从1,2,
3,4,
5五个数字中,任取两数,求两数都是奇数的概率。至少一个奇数呢?
作业
P123
练习1、2
题
