沪教版高中数学高二下册-12.6 双曲线的性质-动点轨迹的探求 教案
文档属性
| 名称 | 沪教版高中数学高二下册-12.6 双曲线的性质-动点轨迹的探求 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 21:19:53 | ||
图片预览

文档简介
动点轨迹的探求
【教学目标】1.加深对圆、椭圆、双曲线的定义的理解,能熟练运用定义法求轨迹方程;
2.在解决问题的过程中,逐渐培养自主探究的意识和能力;
3.通过对问题的变式探究、类比探究以及自主提出问题,初步掌握研究问题的方法,体味数学思维的魅力,提升数学素养.
【教学重点】运用定义法求动点的轨迹
【教学难点】对动点满足条件的理解(转化为定义的过程)
【媒体技术】图形计算器
【问题链简图】
(
核心问题:
用定义法
求动点的轨迹
典例精析,求椭圆的轨迹方程
问题
1
:
变式探究,改变例题中点
B
的
位置
,求动点的轨迹
问题
2
:
逆向探究,从例题的结论出发,需要增加怎样的条件,才能把例题中的条件作为结论
问题
1.
改变点
B
的位置,点
M
的轨迹会发生变化吗?
问题
2.
如果发生了变化,可能有几种情况?
问题
3.
既然发生了变化,如何根据点
B
的位置进行分类?
问题
4.
请用定义法解释每一种轨迹
改变点
P
在线段
MF
1
上的位置,点
M
的轨迹还都是圆吗?
点
P
是线段
MF
1
时,你会求
M
的轨迹方程吗
此时两条线段长度有怎样的等量关系
点
P
在直线
MF
1
的任意位置,你会求
M
的轨迹方程吗
)
【教学过程】
一、复习巩固:(即时调查)前面我们一起学习了圆、椭圆、双曲线的定义及标准方程,现在请同学们完成一组练习,并提交。
1.平面内到两个定点、的距离之和等于8的点的轨迹方程是(
)
A.B.C.D.
2.已知两个定点、,动点满足,则点的轨迹是
(
)
A.
双曲线
B.
双曲线的一支
C.
射线
D.
不存在
二、典例精析:
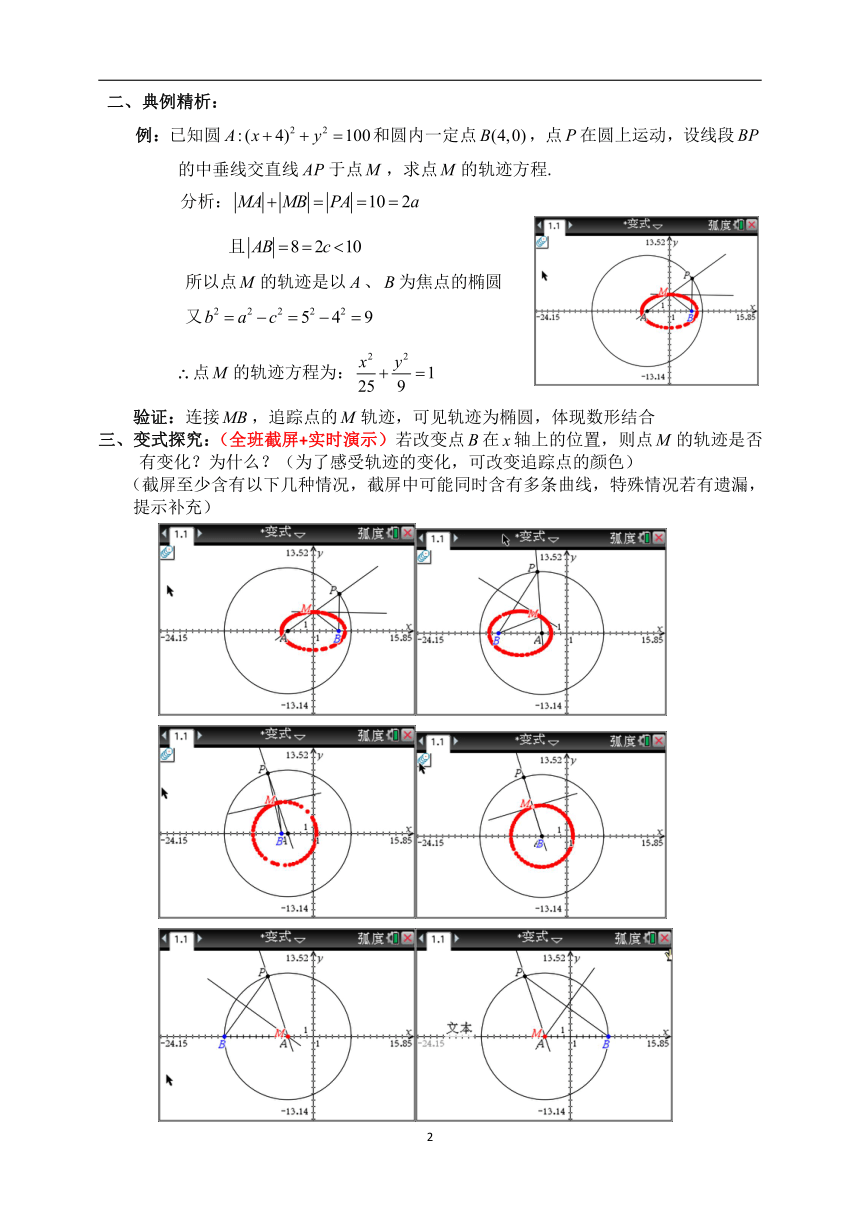
例:已知圆和圆内一定点,点在圆上运动,设线段的中垂线交直线于点,求点的轨迹方程.
分析:
且
所以点的轨迹是以、为焦点的椭圆
又
点的轨迹方程为:
验证:连接,追踪点的轨迹,可见轨迹为椭圆,体现数形结合
三、变式探究:(全班截屏+实时演示)若改变点在轴上的位置,则点的轨迹是否有变化?为什么?(为了感受轨迹的变化,可改变追踪点的颜色)
(截屏至少含有以下几种情况,截屏中可能同时含有多条曲线,特殊情况若有遗漏,提示补充)
总结:当点在圆内(异于点)时,轨迹是以、为焦点的椭圆;
当点与点重合时,轨迹是圆的同心圆,此时中垂线即为圆的切线;
当点在圆上时,轨迹是一个点,即点;
当点在圆外时,轨迹是以、为焦点的双曲线.(请同学用定义法解释)
四、逆向探究:
思考题:已知点在椭圆上运动,、分别为椭圆的左、右焦点,过作的外角平分线所在直线的垂线,交直线于一点,求点的轨迹方程.
分析:
所以点的轨迹是以为圆心的圆
方程为:
(追踪点的轨迹,数形结合)
探究:(实时演示)此时学生可以发现,所谓的思考题就是例1的逆向问题。既然是同一个题目的正、逆两个方面的描述,那么两种描述中的中垂线或者角平分线所在直线就应该是同一条直线,由此请同学们继续探究这条直线相对于椭圆有怎样的特殊身份呢?
引导学生用图形计算器追踪直线扫过的区域,观察并思考直线的特殊身份
结论1:这条直线就是椭圆过点的切线
结论2:由角平分线及对顶角可知,此题揭示了椭圆的光学性质:由椭圆一个焦点发出的光线经过椭圆反射后经过另一个焦点。
此结论在教材第51页英文版的的阅读材料中有描述
此结论可以解释折纸游戏中为什么折出来的是椭圆
此结论亦可解读建筑低音廊的理论依据
五、类比提问:在例1中,当点在圆内时,轨迹可能是椭圆,我们研究了它的逆向问题,请同学们大胆尝试:当点在圆外时,以双曲线为例,你能给出类似的逆向问题吗?
问题:已知点在双曲线上运动,、分别为双曲线的左、右焦点,过作的内角平分线的垂线,交直线于一点,求点的轨迹方程.
分析:
所以点的轨迹是以为圆心的圆
方程为:
(追踪点的轨迹,数形结合)
(实时演示)用图形计算器追踪直线扫过的区域,
观察并思考直线的特殊身份
【课堂小结】图形计算器
【教学反思】通过本节课的学习,同学们除了学习到知识与方法外,还可以领会研究问题的基本思路,学会由一道题向一类题的迁移,学会联系,学会类比,更多的还可以体会数学研究的严谨性、体会数学的运动变化之美、体会数学思维之美。时间分配上还可以调节一下,可以让同学们探究过程再充分一些。
1
【教学目标】1.加深对圆、椭圆、双曲线的定义的理解,能熟练运用定义法求轨迹方程;
2.在解决问题的过程中,逐渐培养自主探究的意识和能力;
3.通过对问题的变式探究、类比探究以及自主提出问题,初步掌握研究问题的方法,体味数学思维的魅力,提升数学素养.
【教学重点】运用定义法求动点的轨迹
【教学难点】对动点满足条件的理解(转化为定义的过程)
【媒体技术】图形计算器
【问题链简图】
(
核心问题:
用定义法
求动点的轨迹
典例精析,求椭圆的轨迹方程
问题
1
:
变式探究,改变例题中点
B
的
位置
,求动点的轨迹
问题
2
:
逆向探究,从例题的结论出发,需要增加怎样的条件,才能把例题中的条件作为结论
问题
1.
改变点
B
的位置,点
M
的轨迹会发生变化吗?
问题
2.
如果发生了变化,可能有几种情况?
问题
3.
既然发生了变化,如何根据点
B
的位置进行分类?
问题
4.
请用定义法解释每一种轨迹
改变点
P
在线段
MF
1
上的位置,点
M
的轨迹还都是圆吗?
点
P
是线段
MF
1
时,你会求
M
的轨迹方程吗
此时两条线段长度有怎样的等量关系
点
P
在直线
MF
1
的任意位置,你会求
M
的轨迹方程吗
)
【教学过程】
一、复习巩固:(即时调查)前面我们一起学习了圆、椭圆、双曲线的定义及标准方程,现在请同学们完成一组练习,并提交。
1.平面内到两个定点、的距离之和等于8的点的轨迹方程是(
)
A.B.C.D.
2.已知两个定点、,动点满足,则点的轨迹是
(
)
A.
双曲线
B.
双曲线的一支
C.
射线
D.
不存在
二、典例精析:
例:已知圆和圆内一定点,点在圆上运动,设线段的中垂线交直线于点,求点的轨迹方程.
分析:
且
所以点的轨迹是以、为焦点的椭圆
又
点的轨迹方程为:
验证:连接,追踪点的轨迹,可见轨迹为椭圆,体现数形结合
三、变式探究:(全班截屏+实时演示)若改变点在轴上的位置,则点的轨迹是否有变化?为什么?(为了感受轨迹的变化,可改变追踪点的颜色)
(截屏至少含有以下几种情况,截屏中可能同时含有多条曲线,特殊情况若有遗漏,提示补充)
总结:当点在圆内(异于点)时,轨迹是以、为焦点的椭圆;
当点与点重合时,轨迹是圆的同心圆,此时中垂线即为圆的切线;
当点在圆上时,轨迹是一个点,即点;
当点在圆外时,轨迹是以、为焦点的双曲线.(请同学用定义法解释)
四、逆向探究:
思考题:已知点在椭圆上运动,、分别为椭圆的左、右焦点,过作的外角平分线所在直线的垂线,交直线于一点,求点的轨迹方程.
分析:
所以点的轨迹是以为圆心的圆
方程为:
(追踪点的轨迹,数形结合)
探究:(实时演示)此时学生可以发现,所谓的思考题就是例1的逆向问题。既然是同一个题目的正、逆两个方面的描述,那么两种描述中的中垂线或者角平分线所在直线就应该是同一条直线,由此请同学们继续探究这条直线相对于椭圆有怎样的特殊身份呢?
引导学生用图形计算器追踪直线扫过的区域,观察并思考直线的特殊身份
结论1:这条直线就是椭圆过点的切线
结论2:由角平分线及对顶角可知,此题揭示了椭圆的光学性质:由椭圆一个焦点发出的光线经过椭圆反射后经过另一个焦点。
此结论在教材第51页英文版的的阅读材料中有描述
此结论可以解释折纸游戏中为什么折出来的是椭圆
此结论亦可解读建筑低音廊的理论依据
五、类比提问:在例1中,当点在圆内时,轨迹可能是椭圆,我们研究了它的逆向问题,请同学们大胆尝试:当点在圆外时,以双曲线为例,你能给出类似的逆向问题吗?
问题:已知点在双曲线上运动,、分别为双曲线的左、右焦点,过作的内角平分线的垂线,交直线于一点,求点的轨迹方程.
分析:
所以点的轨迹是以为圆心的圆
方程为:
(追踪点的轨迹,数形结合)
(实时演示)用图形计算器追踪直线扫过的区域,
观察并思考直线的特殊身份
【课堂小结】图形计算器
【教学反思】通过本节课的学习,同学们除了学习到知识与方法外,还可以领会研究问题的基本思路,学会由一道题向一类题的迁移,学会联系,学会类比,更多的还可以体会数学研究的严谨性、体会数学的运动变化之美、体会数学思维之美。时间分配上还可以调节一下,可以让同学们探究过程再充分一些。
1
