2020年春北师大版数学七年级下 5.2 探索轴对称的性质 同步练习含答案
文档属性
| 名称 | 2020年春北师大版数学七年级下 5.2 探索轴对称的性质 同步练习含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 117.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-05 00:00:00 | ||
图片预览

文档简介
5.2
探索轴对称的性质
一.选择题(共9小题)
1.下列说法错误的是( )
A.关于某直线成轴对称的两个图形一定能完全重合
B.线段是轴对称图形
C.全等的两个三角形一定关于某直线成轴对称
D.轴对称图形的对称轴至少有一条
2.如图,△ABC和△A′B′C′关于直线l对称,若∠A=50°,∠C′=30°,则∠B的度数为( )
A.30°
B.50°
C.90°
D.100°
3.如图,△ABC中,D点在BC上,∠B=62°,∠C=53°,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF.则∠EAF的度数为( )
A.124°
B.115°
C.130°
D.106°
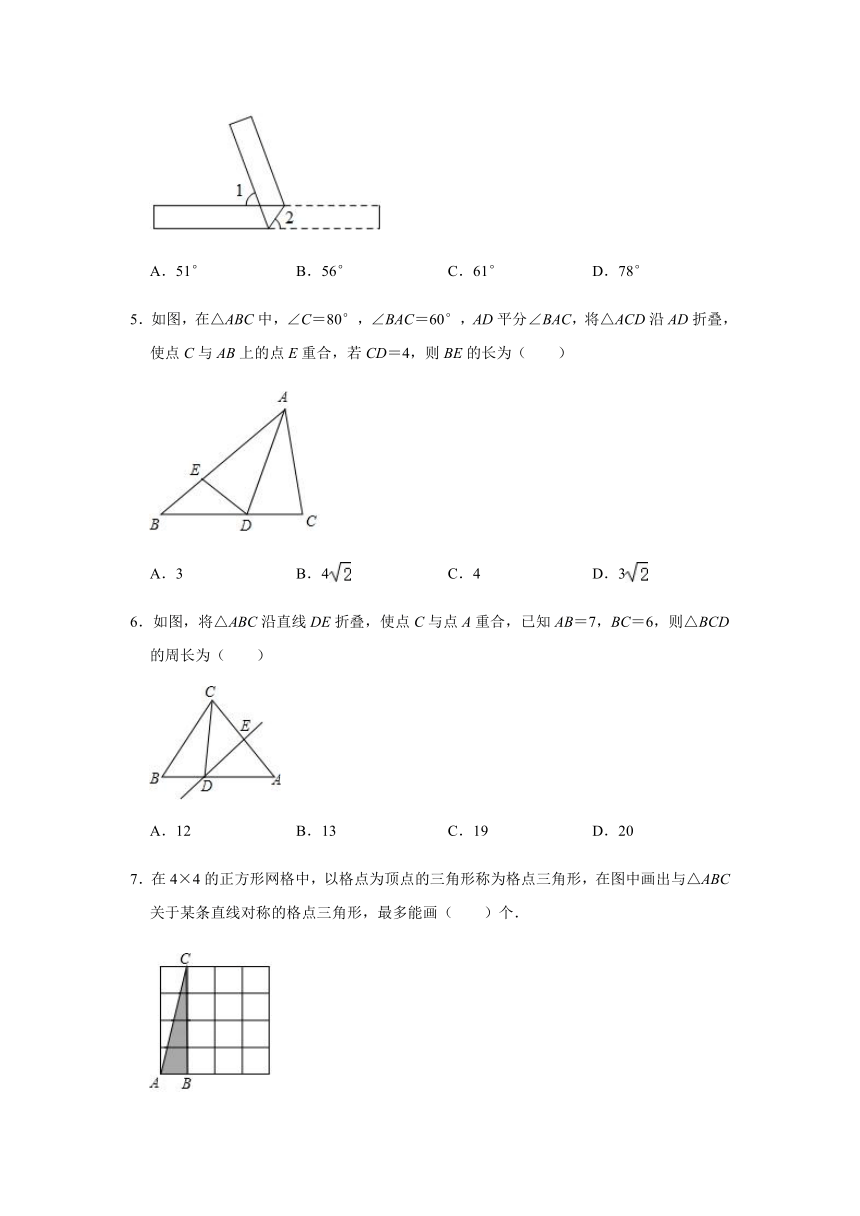
4.如图,将一张矩形纸片折叠,若∠1=78°,则∠2的度数是( )
A.51°
B.56°
C.61°
D.78°
5.如图,在△ABC中,∠C=80°,∠BAC=60°,AD平分∠BAC,将△ACD沿AD折叠,使点C与AB上的点E重合,若CD=4,则BE的长为( )
A.3
B.4
C.4
D.3
6.如图,将△ABC沿直线DE折叠,使点C与点A重合,已知AB=7,BC=6,则△BCD的周长为( )
A.12
B.13
C.19
D.20
7.在4×4的正方形网格中,以格点为顶点的三角形称为格点三角形,在图中画出与△ABC关于某条直线对称的格点三角形,最多能画( )个.
A.5
B.6
C.7
D.8
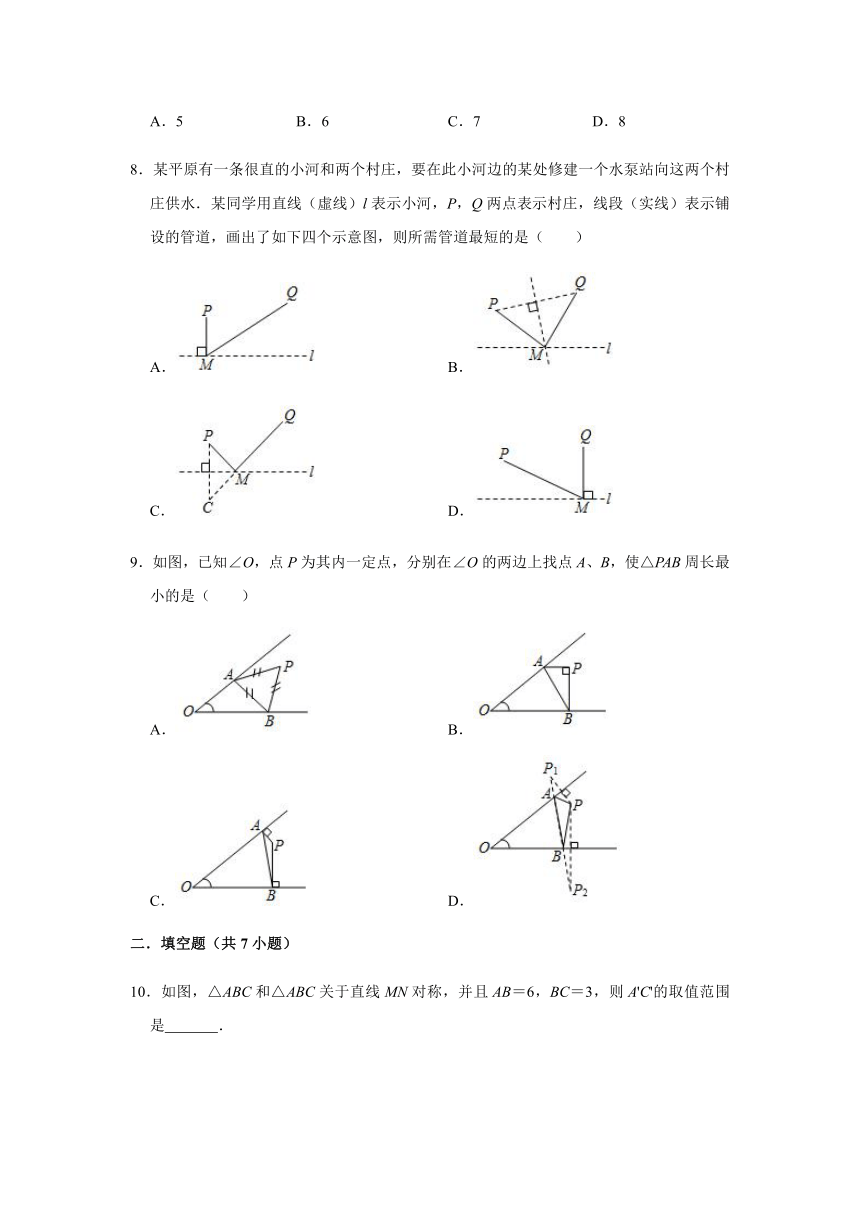
8.某平原有一条很直的小河和两个村庄,要在此小河边的某处修建一个水泵站向这两个村庄供水.某同学用直线(虛线)l表示小河,P,Q两点表示村庄,线段(实线)表示铺设的管道,画出了如下四个示意图,则所需管道最短的是( )
A.
B.
C.
D.
9.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A.
B.
C.
D.
二.填空题(共7小题)
10.如图,△ABC和△ABC关于直线MN对称,并且AB=6,BC=3,则A'C'的取值范围是
.
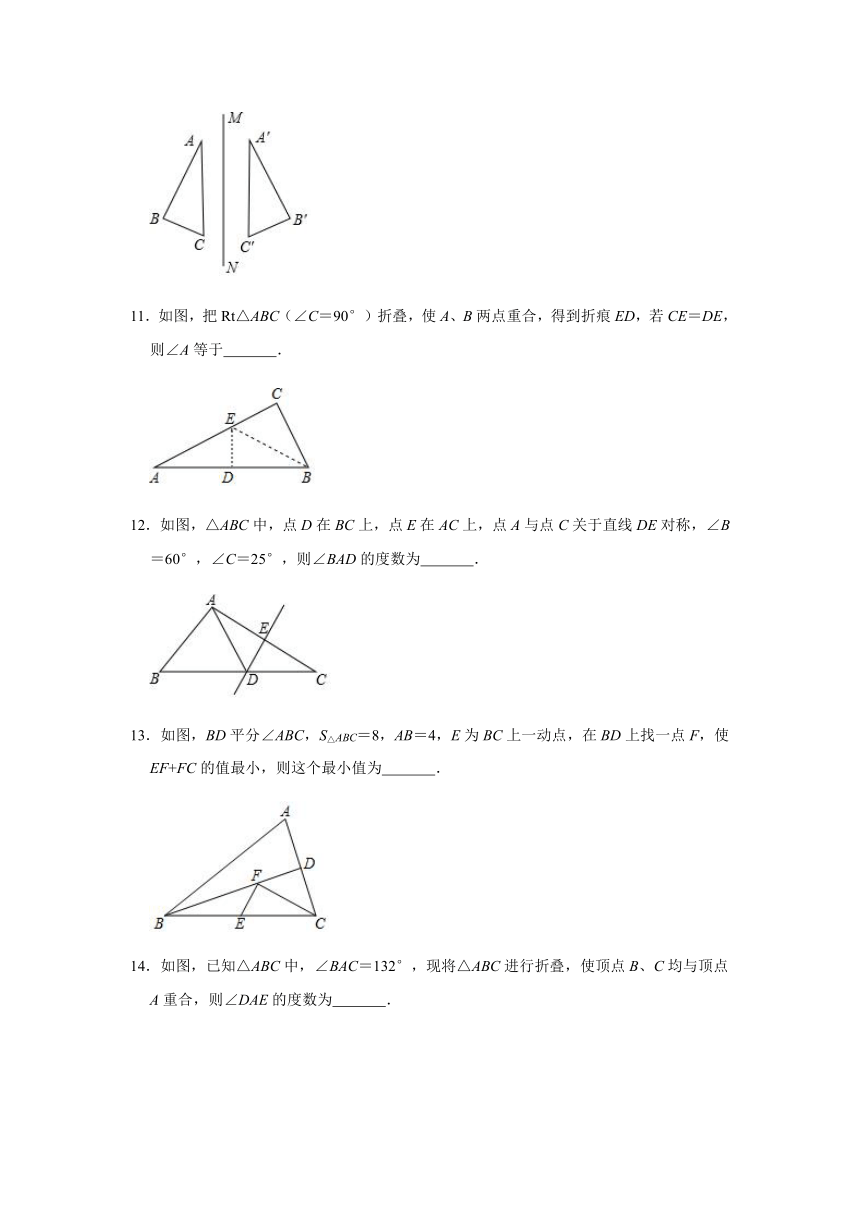
11.如图,把Rt△ABC(∠C=90°)折叠,使A、B两点重合,得到折痕ED,若CE=DE,则∠A等于
.
12.如图,△ABC中,点D在BC上,点E在AC上,点A与点C关于直线DE对称,∠B=60°,∠C=25°,则∠BAD的度数为
.
13.如图,BD平分∠ABC,S△ABC=8,AB=4,E为BC上一动点,在BD上找一点F,使EF+FC的值最小,则这个最小值为
.
14.如图,已知△ABC中,∠BAC=132°,现将△ABC进行折叠,使顶点B、C均与顶点A重合,则∠DAE的度数为
.
15.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,在格纸中能画出与△ABC成轴对称且也以格点为顶点的三角形(不包括△ABC本身),这样的三角形共有
个
16.如图,点P是∠AOB内任意一点,OP=10cm,点P关于射线OA对称点为点P1,点P关于射线OB对称点为点P2,连接P1P2,交OA于点C,交OB于点D,当△PCD的周长是10cm时,∠AOB的度数是
.
三.解答题(共4小题)
17.如图,△ABC中,∠A=90°,D为AC上一点,E为BC上一点,点A和点E关于BD对称,点B和点C关于DE对称.求∠ABC和∠C的度数.
18.如图,在△ABC中,直线l交AB于点M,交BC于点N,点B关于直线l的对称点D在线段BC上,且AD⊥MD,∠B=28°,求∠DAB的度数.
19.如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为14,求△PAB的周长.
20.如图,点P是∠AOB外的一点,点Q是点P关于OA的对称点,点R是点P关于OB的对称点,直线QR分别交∠AOB两边OA,OB于点M,N,连结PM,PN,如果∠PMO=33°,∠PNO=70°,求∠QPN的度数.
参考答案
一.选择题(共9小题)
1.
C.
2.
D.
3.
C.
4.
A.
5.
C.
6.
B.
7.
C.
8.
C.
9.
D.
二.填空题(共7小题)
10.
3<A′C′<9.
11.
30°.
12.
70°.
13.
4.
14.
84°.
15.
3.
16.
30°
三.解答题(共4小题)
17.解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD,
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C,
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°,
∴∠C=30°,
∴∠ABC=2∠C=60°.
18.解:∵点B关于直线l的对称点是点D,
∴直线l是线段DB的垂直平分线,
∴MD=MB,
∴∠MDB=∠B=28°,
∴∠AMD=∠MDB+∠B=56°,
在Rt△ADM中
∠DBA=90°﹣56°=34°.
19.解:∵P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,
∴PA=AG,PB=BH,
∴△PAB的周长=AP+PB+AB=AG+AB+BH=GH=14.
20.解:∵点Q和点P关于OA的对称,
点R和点P关于OB的对称
∴直线OA、OB分别是PQ、PR的中垂线,
∴MP=MQ,NP=NR,
∴∠PMO=∠QMO,∠PNO=∠RNO,
∵∠PMO=3
3°,∠PNO=70°
∴∠PMO=∠QMO=33°,∠PNO=∠RNO=70°
∴∠PMQ=66°,∠PNR=140°
∴∠MQP=57°,
∴∠PQN=123°,∠PNQ=40°,
∴∠QPN=17°.
探索轴对称的性质
一.选择题(共9小题)
1.下列说法错误的是( )
A.关于某直线成轴对称的两个图形一定能完全重合
B.线段是轴对称图形
C.全等的两个三角形一定关于某直线成轴对称
D.轴对称图形的对称轴至少有一条
2.如图,△ABC和△A′B′C′关于直线l对称,若∠A=50°,∠C′=30°,则∠B的度数为( )
A.30°
B.50°
C.90°
D.100°
3.如图,△ABC中,D点在BC上,∠B=62°,∠C=53°,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF.则∠EAF的度数为( )
A.124°
B.115°
C.130°
D.106°
4.如图,将一张矩形纸片折叠,若∠1=78°,则∠2的度数是( )
A.51°
B.56°
C.61°
D.78°
5.如图,在△ABC中,∠C=80°,∠BAC=60°,AD平分∠BAC,将△ACD沿AD折叠,使点C与AB上的点E重合,若CD=4,则BE的长为( )
A.3
B.4
C.4
D.3
6.如图,将△ABC沿直线DE折叠,使点C与点A重合,已知AB=7,BC=6,则△BCD的周长为( )
A.12
B.13
C.19
D.20
7.在4×4的正方形网格中,以格点为顶点的三角形称为格点三角形,在图中画出与△ABC关于某条直线对称的格点三角形,最多能画( )个.
A.5
B.6
C.7
D.8
8.某平原有一条很直的小河和两个村庄,要在此小河边的某处修建一个水泵站向这两个村庄供水.某同学用直线(虛线)l表示小河,P,Q两点表示村庄,线段(实线)表示铺设的管道,画出了如下四个示意图,则所需管道最短的是( )
A.
B.
C.
D.
9.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A.
B.
C.
D.
二.填空题(共7小题)
10.如图,△ABC和△ABC关于直线MN对称,并且AB=6,BC=3,则A'C'的取值范围是
.
11.如图,把Rt△ABC(∠C=90°)折叠,使A、B两点重合,得到折痕ED,若CE=DE,则∠A等于
.
12.如图,△ABC中,点D在BC上,点E在AC上,点A与点C关于直线DE对称,∠B=60°,∠C=25°,则∠BAD的度数为
.
13.如图,BD平分∠ABC,S△ABC=8,AB=4,E为BC上一动点,在BD上找一点F,使EF+FC的值最小,则这个最小值为
.
14.如图,已知△ABC中,∠BAC=132°,现将△ABC进行折叠,使顶点B、C均与顶点A重合,则∠DAE的度数为
.
15.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,在格纸中能画出与△ABC成轴对称且也以格点为顶点的三角形(不包括△ABC本身),这样的三角形共有
个
16.如图,点P是∠AOB内任意一点,OP=10cm,点P关于射线OA对称点为点P1,点P关于射线OB对称点为点P2,连接P1P2,交OA于点C,交OB于点D,当△PCD的周长是10cm时,∠AOB的度数是
.
三.解答题(共4小题)
17.如图,△ABC中,∠A=90°,D为AC上一点,E为BC上一点,点A和点E关于BD对称,点B和点C关于DE对称.求∠ABC和∠C的度数.
18.如图,在△ABC中,直线l交AB于点M,交BC于点N,点B关于直线l的对称点D在线段BC上,且AD⊥MD,∠B=28°,求∠DAB的度数.
19.如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为14,求△PAB的周长.
20.如图,点P是∠AOB外的一点,点Q是点P关于OA的对称点,点R是点P关于OB的对称点,直线QR分别交∠AOB两边OA,OB于点M,N,连结PM,PN,如果∠PMO=33°,∠PNO=70°,求∠QPN的度数.
参考答案
一.选择题(共9小题)
1.
C.
2.
D.
3.
C.
4.
A.
5.
C.
6.
B.
7.
C.
8.
C.
9.
D.
二.填空题(共7小题)
10.
3<A′C′<9.
11.
30°.
12.
70°.
13.
4.
14.
84°.
15.
3.
16.
30°
三.解答题(共4小题)
17.解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD,
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C,
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°,
∴∠C=30°,
∴∠ABC=2∠C=60°.
18.解:∵点B关于直线l的对称点是点D,
∴直线l是线段DB的垂直平分线,
∴MD=MB,
∴∠MDB=∠B=28°,
∴∠AMD=∠MDB+∠B=56°,
在Rt△ADM中
∠DBA=90°﹣56°=34°.
19.解:∵P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,
∴PA=AG,PB=BH,
∴△PAB的周长=AP+PB+AB=AG+AB+BH=GH=14.
20.解:∵点Q和点P关于OA的对称,
点R和点P关于OB的对称
∴直线OA、OB分别是PQ、PR的中垂线,
∴MP=MQ,NP=NR,
∴∠PMO=∠QMO,∠PNO=∠RNO,
∵∠PMO=3
3°,∠PNO=70°
∴∠PMO=∠QMO=33°,∠PNO=∠RNO=70°
∴∠PMQ=66°,∠PNR=140°
∴∠MQP=57°,
∴∠PQN=123°,∠PNQ=40°,
∴∠QPN=17°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
