人教版数学七年级下册第6章实数考点复习课件(共24张PPT)
文档属性
| 名称 | 人教版数学七年级下册第6章实数考点复习课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
第六章:实数
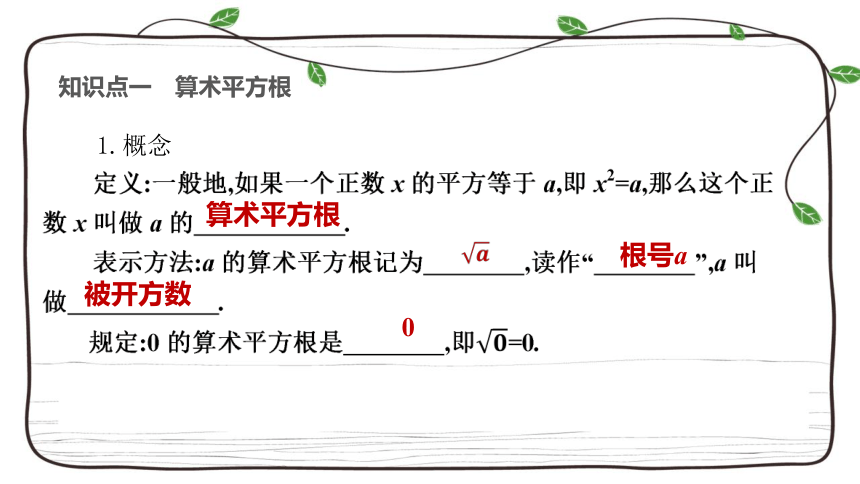
知识点一 算术平方根
算术平方根
根号a
0
被开方数
1.概念
2.1算数平方根的性质
2.2算数平方根具有双重非负性
非负数
非负数
知识点二.
平方根的定义及表示方法
平方根
二次方根
平方根
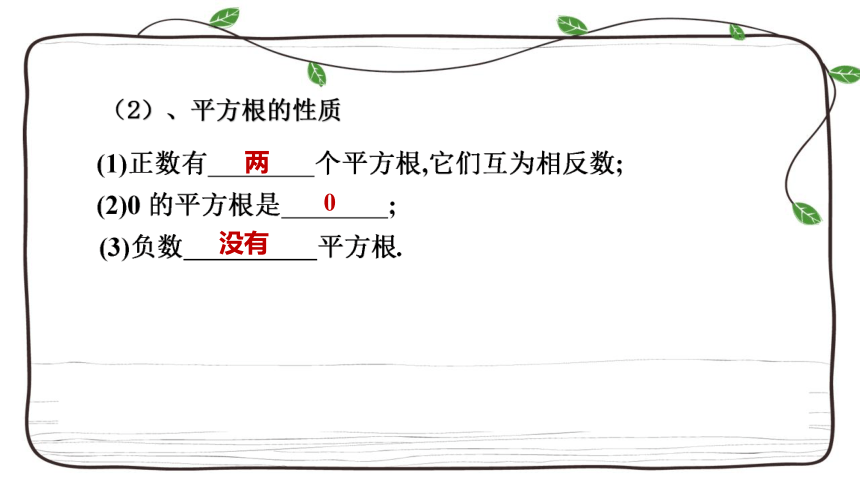
(2)、平方根的性质
两
0
没有
题型一:平方根,算数平方根的概念及其表示
例1.判断下列说法是否正确
(1)5是(-5)?的算数平方根
(2)4是2的算数平方根
(3)7是
的算数平方根
(4)
的平方根是±7
(5)平方根等于本身的数是0和1
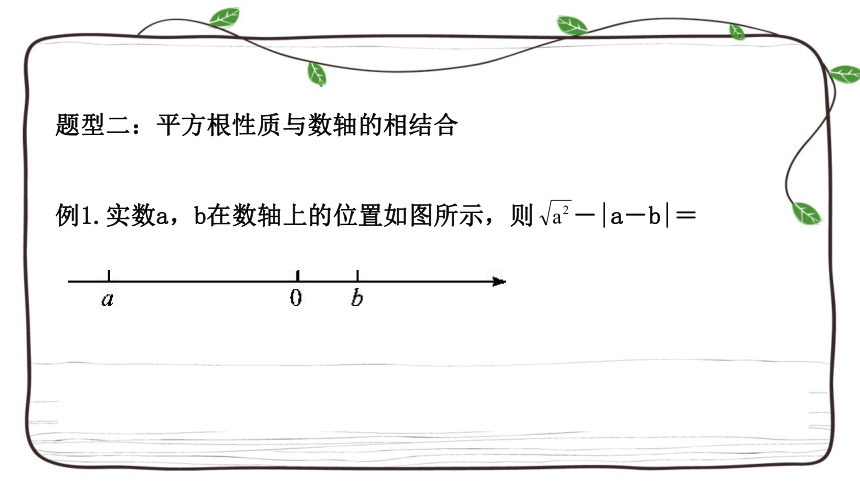
题型二:平方根性质与数轴的相结合
例1.实数a,b在数轴上的位置如图所示,则
-|a-b|=
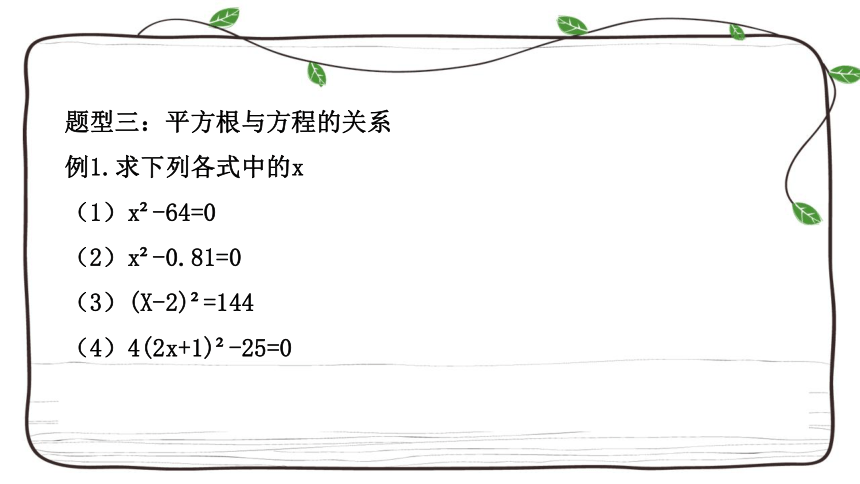
题型三:平方根与方程的关系
例1.求下列各式中的x
(1)x?-64=0
(2)x?-0.81=0
(3)(X-2)?=144
(4)4(2x+1)?-25=0
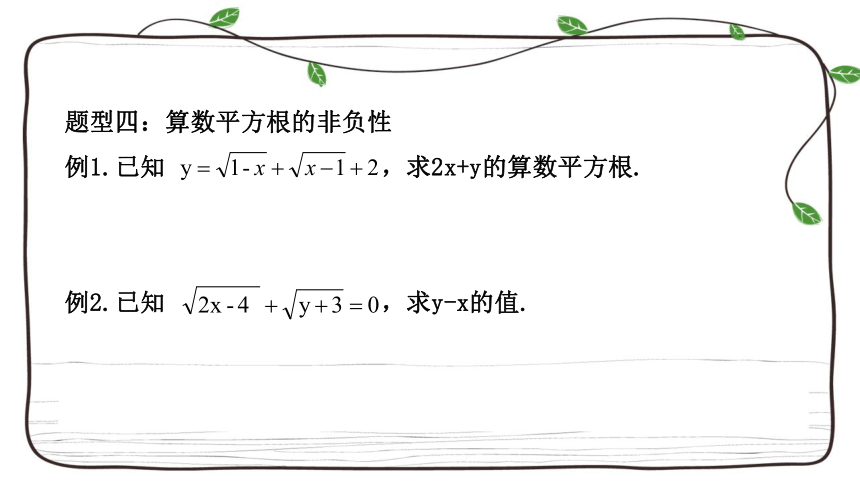
题型四:算数平方根的非负性
例1.已知
,求2x+y的算数平方根.
例2.已知
,求y-x的值.
题型五:平方根的估算
例1.已知a,b为两个连续的整数,且a<
练习一
2.a的算术平方根是3,b是16的算术平方根,则a+b=____.
3.
4.
5.
6.计算
知识点三
立方根
立方根
正数
负数
0
3.立方根的性质
2.开立方的概念:
1.立方根的概念:一般的,如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根,也就是说,如果x?=a,那么x叫做a的立方根
练习2.
练习3.
(1)8x?+125=0
(2)(x+3)?
-8=0
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根
平方根
立方根
表示方法
的取值
性
质
≥
开方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身的数
0,1
0
0,1,-1
实数
有理数
无理数
整数
分数
有限小数和无限循环小数
无限不循环小数
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
1.有理数和无理数统称实数.
实数的分类
2.实数范围内的相关概念
-a
本身
相反数
0
a
0
-a
例1.把下列各数分别填入相应的括号内:
;
;
;
;
2兀-1;
0;
-0.5;
0.12112111211112......
有理数集合:{
}
无理数集合:{
}
整数集合:
{
}
分数集合:
{
}
正实数集合:{
}
负实数集合:{
}
例2.
判断:下列说法是否正确:
1.实数不是有理数就是无理数。
(
)
2.无限小数都是无理数。
(
)
3.无理数都是无限小数。
(
)
4.带根号的数都是无理数。
(
)
5.两个无理数之和一定是无理数。
(
)
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。
(
)
练习1.
和数轴上的点一一对应的是(
)
A.整数
B.有理数
C.无理数
D.实数
练习2.
的整数部分是___________;小数部分是_____________.
练习3.
比较2,
,
的大小,按从小到大排列______________.
【课堂小结】
【出门测】
1.
等于(
)
A.3
B.-3
C.-2
D.2
2.
的的平方根是(
)
A.±4
B.4
C.±2
D.2
3.若一个数的平方根是2a-4和3a+9,求这个数是_______.
4.若
=15,
=150,则x=_______.
【出门测】
4.
a+b=0.则
=_________.
5.求下列各式中x的值.
(1).2(3x-1)?=8
(2).(x+1)?-64=0
6.如果x与y满足
,求x+y的值.
谢
谢
观
看
第六章:实数
知识点一 算术平方根
算术平方根
根号a
0
被开方数
1.概念
2.1算数平方根的性质
2.2算数平方根具有双重非负性
非负数
非负数
知识点二.
平方根的定义及表示方法
平方根
二次方根
平方根
(2)、平方根的性质
两
0
没有
题型一:平方根,算数平方根的概念及其表示
例1.判断下列说法是否正确
(1)5是(-5)?的算数平方根
(2)4是2的算数平方根
(3)7是
的算数平方根
(4)
的平方根是±7
(5)平方根等于本身的数是0和1
题型二:平方根性质与数轴的相结合
例1.实数a,b在数轴上的位置如图所示,则
-|a-b|=
题型三:平方根与方程的关系
例1.求下列各式中的x
(1)x?-64=0
(2)x?-0.81=0
(3)(X-2)?=144
(4)4(2x+1)?-25=0
题型四:算数平方根的非负性
例1.已知
,求2x+y的算数平方根.
例2.已知
,求y-x的值.
题型五:平方根的估算
例1.已知a,b为两个连续的整数,且a<
2.a的算术平方根是3,b是16的算术平方根,则a+b=____.
3.
4.
5.
6.计算
知识点三
立方根
立方根
正数
负数
0
3.立方根的性质
2.开立方的概念:
1.立方根的概念:一般的,如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根,也就是说,如果x?=a,那么x叫做a的立方根
练习2.
练习3.
(1)8x?+125=0
(2)(x+3)?
-8=0
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根
平方根
立方根
表示方法
的取值
性
质
≥
开方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是本身的数
0,1
0
0,1,-1
实数
有理数
无理数
整数
分数
有限小数和无限循环小数
无限不循环小数
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
1.有理数和无理数统称实数.
实数的分类
2.实数范围内的相关概念
-a
本身
相反数
0
a
0
-a
例1.把下列各数分别填入相应的括号内:
;
;
;
;
2兀-1;
0;
-0.5;
0.12112111211112......
有理数集合:{
}
无理数集合:{
}
整数集合:
{
}
分数集合:
{
}
正实数集合:{
}
负实数集合:{
}
例2.
判断:下列说法是否正确:
1.实数不是有理数就是无理数。
(
)
2.无限小数都是无理数。
(
)
3.无理数都是无限小数。
(
)
4.带根号的数都是无理数。
(
)
5.两个无理数之和一定是无理数。
(
)
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。
(
)
练习1.
和数轴上的点一一对应的是(
)
A.整数
B.有理数
C.无理数
D.实数
练习2.
的整数部分是___________;小数部分是_____________.
练习3.
比较2,
,
的大小,按从小到大排列______________.
【课堂小结】
【出门测】
1.
等于(
)
A.3
B.-3
C.-2
D.2
2.
的的平方根是(
)
A.±4
B.4
C.±2
D.2
3.若一个数的平方根是2a-4和3a+9,求这个数是_______.
4.若
=15,
=150,则x=_______.
【出门测】
4.
a+b=0.则
=_________.
5.求下列各式中x的值.
(1).2(3x-1)?=8
(2).(x+1)?-64=0
6.如果x与y满足
,求x+y的值.
谢
谢
观
看
