北师大版数学八年级下册6.2.2 平行四边形的判定课件(共14张PPT)
文档属性
| 名称 | 北师大版数学八年级下册6.2.2 平行四边形的判定课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 20:55:36 | ||
图片预览


文档简介
(共14张PPT)
第六章
平行四边形
6.2.2
平行四边形的判定
学
习
目
标
1.理解对角线互相平分的四边形是平行四边形这一判定定理,能够证明并学会简单运用;
2.掌握平行四边形判定的方法.
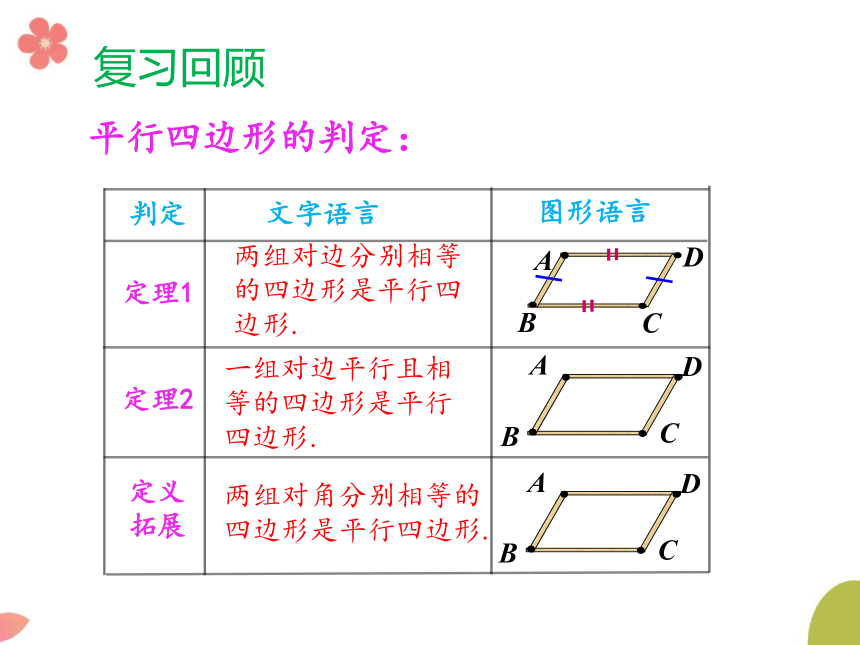
平行四边形的判定:
判定
文字语言
图形语言
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
A
B
C
D
定理1
定理2
定义
拓展
两组对角分别相等的四边形是平行四边形.
A
B
C
D
A
B
C
D
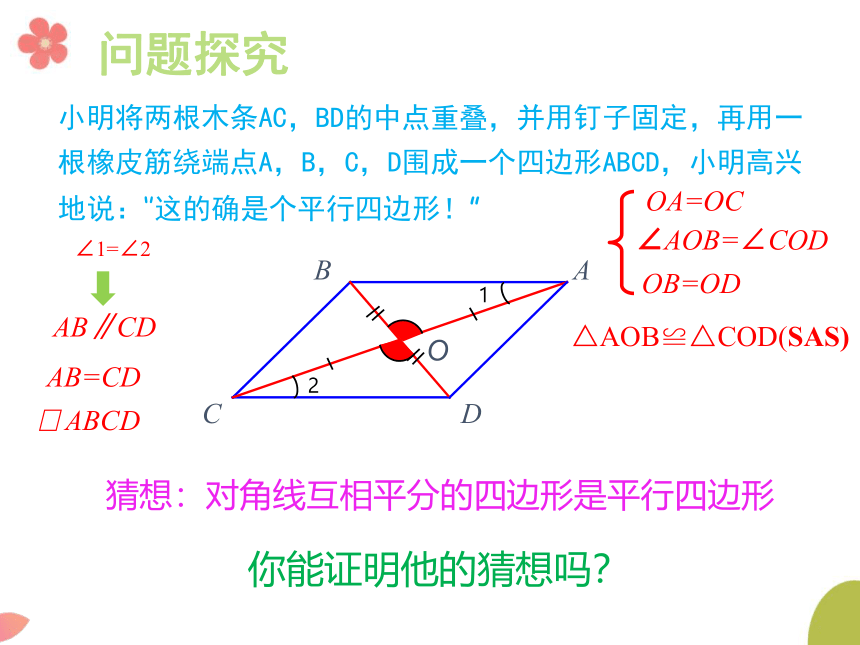
复习回顾
小明将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD,小明高兴地说:‘’这的确是个平行四边形!”
问题探究
猜想:对角线互相平分的四边形是平行四边形
你能证明他的猜想吗?
C
A
B
O
D
OA=OC
OB=OD
∠AOB=∠COD
1
2
∠1=∠2
AB∥CD
AB=CD
ABCD
△AOB≌△COD(SAS)
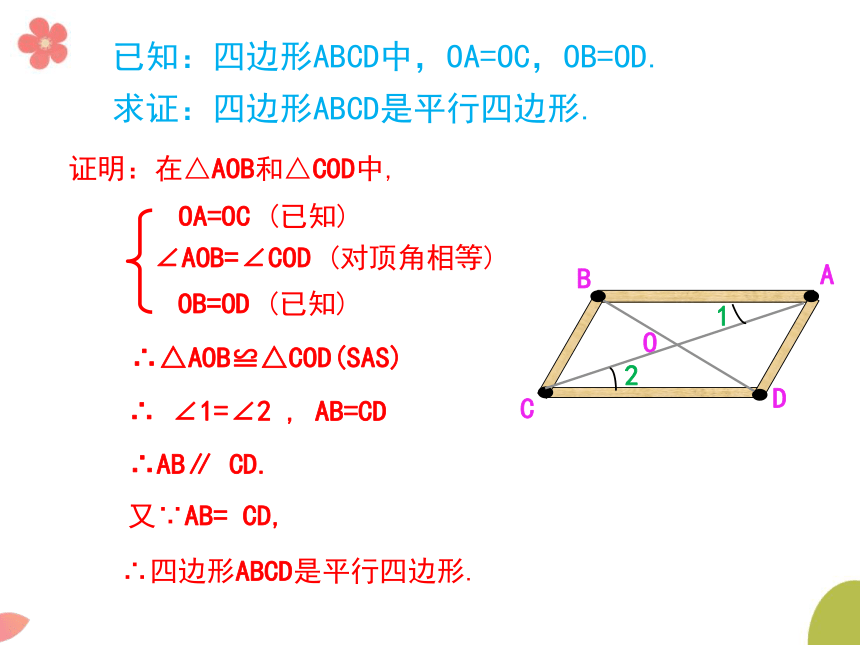
证明:在△AOB和△COD中,
OA=OC
(已知)
∠AOB=∠COD
(对顶角相等)
OB=OD
(已知)
∴△AOB≌△COD(SAS)
∴
∠1=∠2
,
AB=CD
∴AB∥
CD.
又∵AB=
CD,
∴四边形ABCD是平行四边形.
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
A
B
C
D
O
2
1
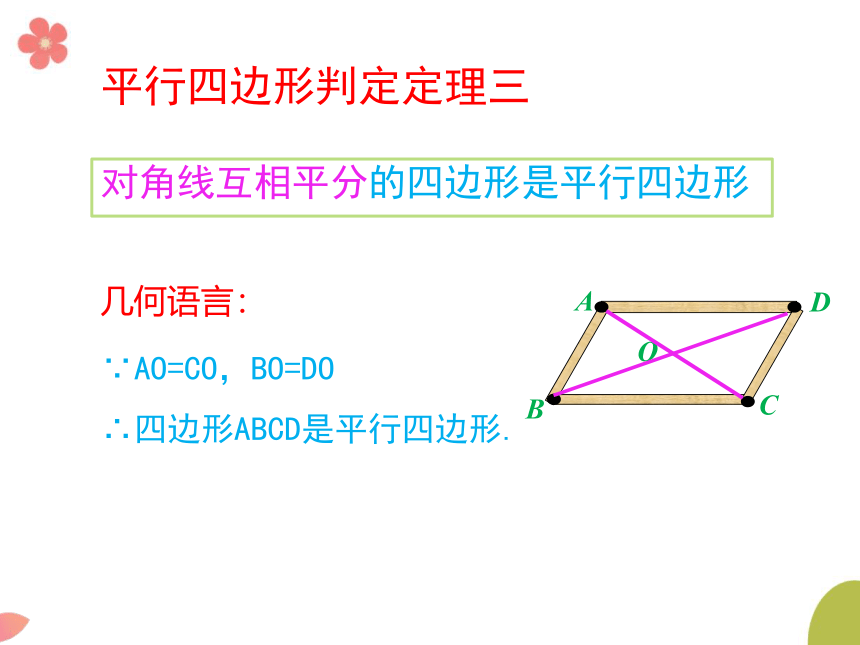
几何语言:
∵AO=CO,BO=DO
∴四边形ABCD是平行四边形.
A
B
C
D
O
对角线互相平分的四边形是平行四边形
平行四边形判定定理三
B
D
A
C
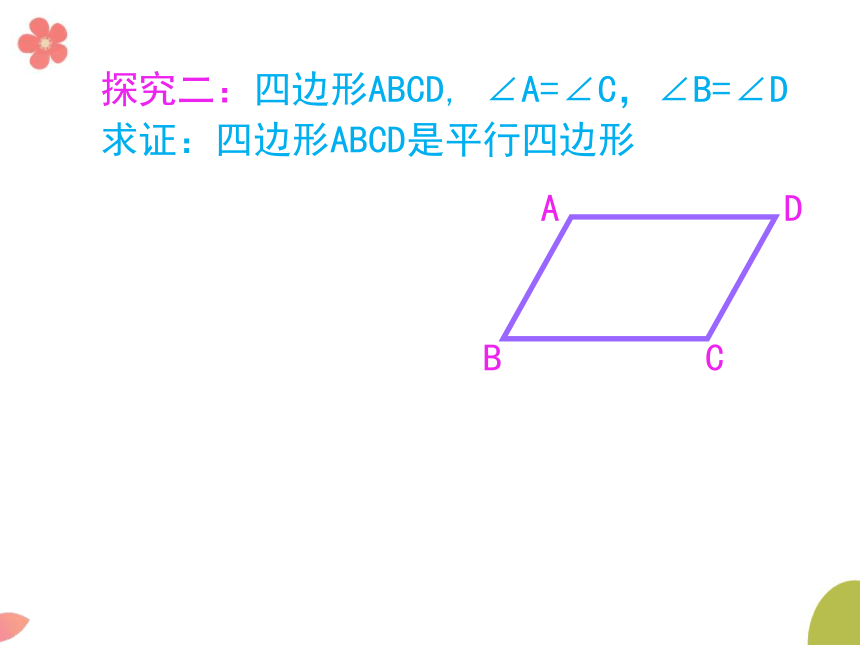
探究二:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
平行四边形的判定定理四
A
B
C
D
两组对角分别相等的四边形是平行四边形
几何语言:
∵
∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形.
1.在下列条件中,能判定四边形ABCD为平行四边形的是(
)
A.AB=AD,CB=CD
B.AB∥CD,AD=BC
D.∠A=∠B,∠C=∠D
C.AB∥CD,AB=CD
A
B
C
D
C
随堂练习
2.
根据下列条件,不能判定一个四边形为平行四边形的是(
)
A.
两组对边分别相等
B
.
两条对角线互相平分
C
.
两条对角线相等
D
.
两组对边分别平行
D
A
B
C
C
(1)若AB//CD,补充条件
,使四边形ABCD为平行四边形;
(2)若AB=CD,补充条件
,使四边形ABCD为平行四边形;
(3)若对角线AC、BD交于点O,OA=OC=3,OB=5,
补充条件
,使四边形ABCD为平行四边形.
3.填空:如图在四边形ABCD中
B
O
D
A
C
AD//BC或AB=CD
AD=BC或AB∥CD
OD=5
(答案不唯一,填一种即可)
4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
B
A
C
E
F
D
O
AO=CO
,BO=DO
EO=FO
AO=CO,
AE=CF,
AO-AE=CO-CF
①
②
③
④
4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
∴AO-AE=CO-CF
证明:连接BD,交AC于点O
∵四边形ABCD是平行四边形
∵AE=CF
即EO=FO
∴
四边形BFDE是平行四边形.
∴AO=CO,BO=DO
B
A
C
E
F
D
O
平行四边形的判定方法
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
两组对角分别相等的四边形是平行四边形(定义拓展)
从对角线考虑
对角线互相平分的四边形是平行四边形(判定定理3)
三个角度,三条定理,五种方法
小结
第六章
平行四边形
6.2.2
平行四边形的判定
学
习
目
标
1.理解对角线互相平分的四边形是平行四边形这一判定定理,能够证明并学会简单运用;
2.掌握平行四边形判定的方法.
平行四边形的判定:
判定
文字语言
图形语言
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
A
B
C
D
定理1
定理2
定义
拓展
两组对角分别相等的四边形是平行四边形.
A
B
C
D
A
B
C
D
复习回顾
小明将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD,小明高兴地说:‘’这的确是个平行四边形!”
问题探究
猜想:对角线互相平分的四边形是平行四边形
你能证明他的猜想吗?
C
A
B
O
D
OA=OC
OB=OD
∠AOB=∠COD
1
2
∠1=∠2
AB∥CD
AB=CD
ABCD
△AOB≌△COD(SAS)
证明:在△AOB和△COD中,
OA=OC
(已知)
∠AOB=∠COD
(对顶角相等)
OB=OD
(已知)
∴△AOB≌△COD(SAS)
∴
∠1=∠2
,
AB=CD
∴AB∥
CD.
又∵AB=
CD,
∴四边形ABCD是平行四边形.
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
A
B
C
D
O
2
1
几何语言:
∵AO=CO,BO=DO
∴四边形ABCD是平行四边形.
A
B
C
D
O
对角线互相平分的四边形是平行四边形
平行四边形判定定理三
B
D
A
C
探究二:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
平行四边形的判定定理四
A
B
C
D
两组对角分别相等的四边形是平行四边形
几何语言:
∵
∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形.
1.在下列条件中,能判定四边形ABCD为平行四边形的是(
)
A.AB=AD,CB=CD
B.AB∥CD,AD=BC
D.∠A=∠B,∠C=∠D
C.AB∥CD,AB=CD
A
B
C
D
C
随堂练习
2.
根据下列条件,不能判定一个四边形为平行四边形的是(
)
A.
两组对边分别相等
B
.
两条对角线互相平分
C
.
两条对角线相等
D
.
两组对边分别平行
D
A
B
C
C
(1)若AB//CD,补充条件
,使四边形ABCD为平行四边形;
(2)若AB=CD,补充条件
,使四边形ABCD为平行四边形;
(3)若对角线AC、BD交于点O,OA=OC=3,OB=5,
补充条件
,使四边形ABCD为平行四边形.
3.填空:如图在四边形ABCD中
B
O
D
A
C
AD//BC或AB=CD
AD=BC或AB∥CD
OD=5
(答案不唯一,填一种即可)
4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
B
A
C
E
F
D
O
AO=CO
,BO=DO
EO=FO
AO=CO,
AE=CF,
AO-AE=CO-CF
①
②
③
④
4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
∴AO-AE=CO-CF
证明:连接BD,交AC于点O
∵四边形ABCD是平行四边形
∵AE=CF
即EO=FO
∴
四边形BFDE是平行四边形.
∴AO=CO,BO=DO
B
A
C
E
F
D
O
平行四边形的判定方法
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
两组对角分别相等的四边形是平行四边形(定义拓展)
从对角线考虑
对角线互相平分的四边形是平行四边形(判定定理3)
三个角度,三条定理,五种方法
小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
