北师大版数学八年级下册6.4.1 多边形的内角和课件(共15张)
文档属性
| 名称 | 北师大版数学八年级下册6.4.1 多边形的内角和课件(共15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
第六章
平行四边形
6.4.1
多边形的内角和
学
习
目
标
1.经历探索多边形内角和的过程,掌握多边形内
角和公式.
2.灵活运用公式进行内角和的计算,并且会计算
正多边形的一个内角的度数.
定义:在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形
复习回顾
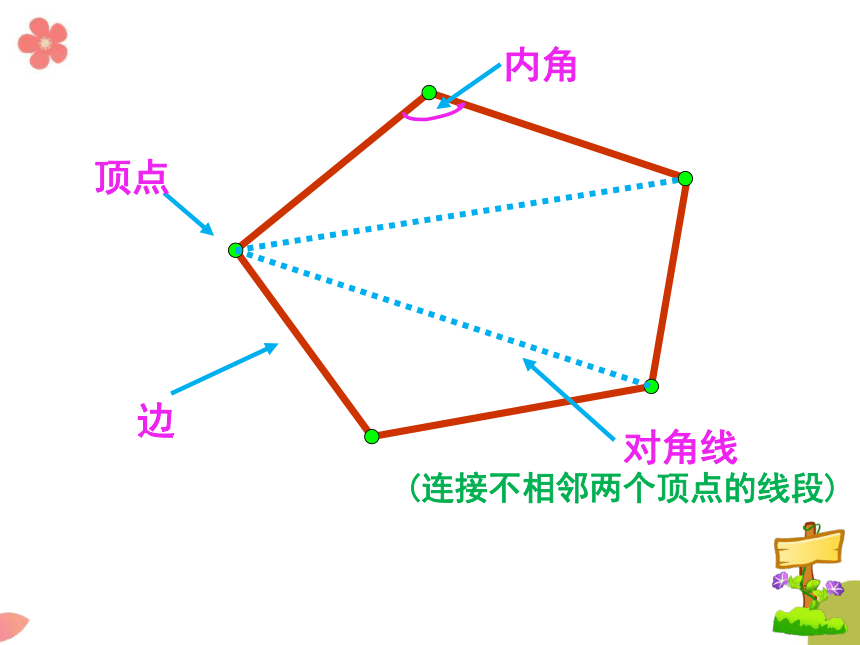
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
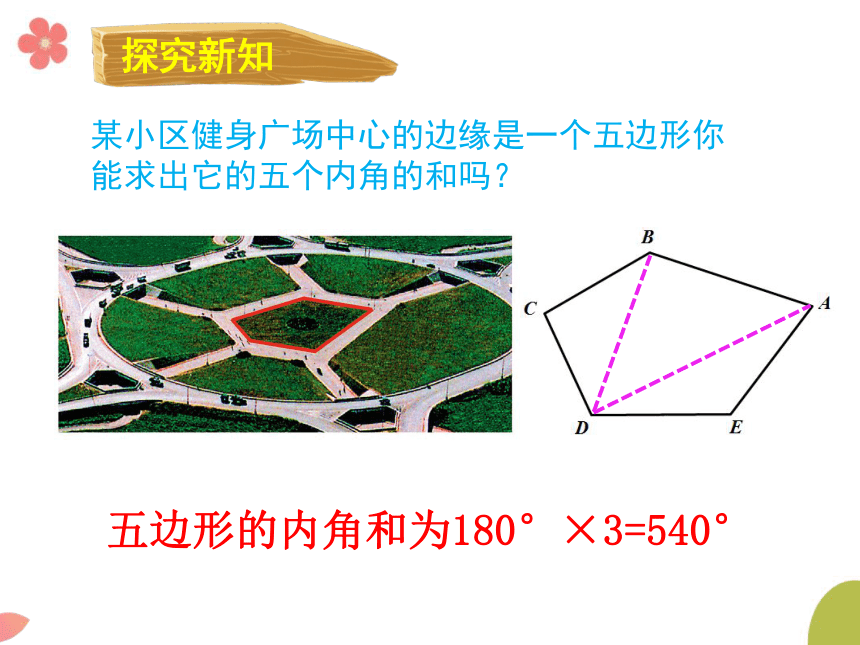
某小区健身广场中心的边缘是一个五边形你能求出它的五个内角的和吗?
五边形的内角和为180°×3=540°
探究新知
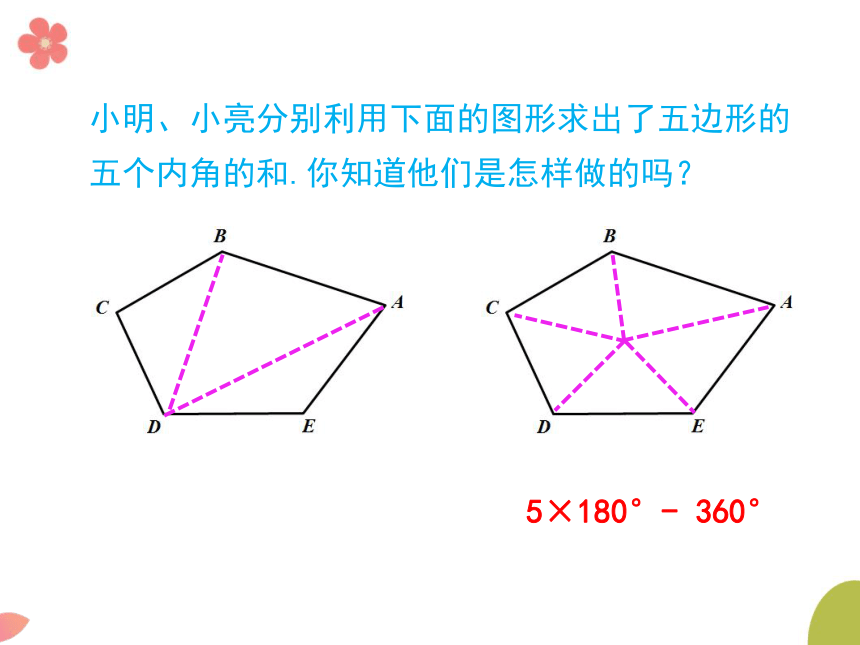
小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
5×180°-
360°
(n-2)×1800
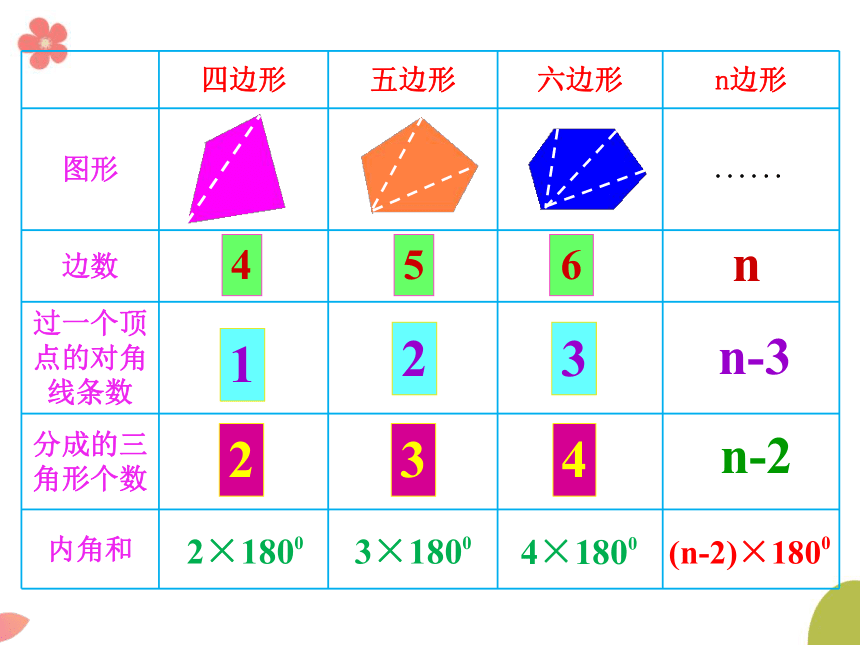
四边形
五边形
六边形
n边形
图形
......
边数
过一个顶点的对角线条数
分成的三角形个数
内角和
n
n-3
n-2
3×1800
4×1800
1
2
3
2
3
4
4
5
6
2×1800
n边形的内角和等于(n-2)·180°
多边形内角和定理:
例1、如图,在四边形ABCD中,∠A+∠C=180°,∠B与∠D有怎样的关系?
如果四边形一组对角互补,那么另一组对角也互补
解:∵在四边形ABCD中,∠A+∠C
=180°
又∵∠A+∠B+∠C+∠D
=(4-2)
×180°=
360°
∴
∠B+∠D
=360°-(∠A+∠C)
=360°-180°=180°
观察图中的多边形,它们的边、角有什么特点?
想一想
在平面内,每个内角都相等、每条边也都相等的多边形叫做正多边形
正n边形的每个内角度数为:
正三角形
正方形
正五边形
正六边形
正八边形
60°
90°
108°
120°
135°
1.八边形的内角和是( )
A.1080°
B.1440°
C.720°
D.900°
2.一个多边形的每个内角均为120°,则这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
A
C
随堂练习
3.正十边形的一个内角的度数是
度.
144
解:
∵多边形为正十边形
∴内角和为(n-2)
×180
°
=(10-2)
×180
°
=
1440
°
∴
一个内角度数为1440°÷10=144°
4.多边形的边数增加一条,内角和就增加______.
180°
5、已知一个多边形,它的内角和等于720°
求这个多边形的边数。
解:
设多边形的边数为n,
由已知,得:
(n-2)?180°=
720°
解得:
n=
6
?这个多边形的边数为6
6、多边形的内角和可能是630°吗?
解:
设多边形的边数为n,由题意得:
(n-2)?180°=
630?
解得:
n=5.5
?n不是整数,所以多边形内角和不可能是630°
多边形内角和
(n-2)
·180°
“n边形”内角和公式
方法
已知边数求内角和:代入法
已知内角和求边数:方程法
正n边形每个内角度数
小结
第六章
平行四边形
6.4.1
多边形的内角和
学
习
目
标
1.经历探索多边形内角和的过程,掌握多边形内
角和公式.
2.灵活运用公式进行内角和的计算,并且会计算
正多边形的一个内角的度数.
定义:在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形
复习回顾
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
某小区健身广场中心的边缘是一个五边形你能求出它的五个内角的和吗?
五边形的内角和为180°×3=540°
探究新知
小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
5×180°-
360°
(n-2)×1800
四边形
五边形
六边形
n边形
图形
......
边数
过一个顶点的对角线条数
分成的三角形个数
内角和
n
n-3
n-2
3×1800
4×1800
1
2
3
2
3
4
4
5
6
2×1800
n边形的内角和等于(n-2)·180°
多边形内角和定理:
例1、如图,在四边形ABCD中,∠A+∠C=180°,∠B与∠D有怎样的关系?
如果四边形一组对角互补,那么另一组对角也互补
解:∵在四边形ABCD中,∠A+∠C
=180°
又∵∠A+∠B+∠C+∠D
=(4-2)
×180°=
360°
∴
∠B+∠D
=360°-(∠A+∠C)
=360°-180°=180°
观察图中的多边形,它们的边、角有什么特点?
想一想
在平面内,每个内角都相等、每条边也都相等的多边形叫做正多边形
正n边形的每个内角度数为:
正三角形
正方形
正五边形
正六边形
正八边形
60°
90°
108°
120°
135°
1.八边形的内角和是( )
A.1080°
B.1440°
C.720°
D.900°
2.一个多边形的每个内角均为120°,则这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
A
C
随堂练习
3.正十边形的一个内角的度数是
度.
144
解:
∵多边形为正十边形
∴内角和为(n-2)
×180
°
=(10-2)
×180
°
=
1440
°
∴
一个内角度数为1440°÷10=144°
4.多边形的边数增加一条,内角和就增加______.
180°
5、已知一个多边形,它的内角和等于720°
求这个多边形的边数。
解:
设多边形的边数为n,
由已知,得:
(n-2)?180°=
720°
解得:
n=
6
?这个多边形的边数为6
6、多边形的内角和可能是630°吗?
解:
设多边形的边数为n,由题意得:
(n-2)?180°=
630?
解得:
n=5.5
?n不是整数,所以多边形内角和不可能是630°
多边形内角和
(n-2)
·180°
“n边形”内角和公式
方法
已知边数求内角和:代入法
已知内角和求边数:方程法
正n边形每个内角度数
小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
