湘教版九年级数学下册第2章 圆 单元测试(3)(含答案)
文档属性
| 名称 | 湘教版九年级数学下册第2章 圆 单元测试(3)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 254.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 09:17:37 | ||
图片预览

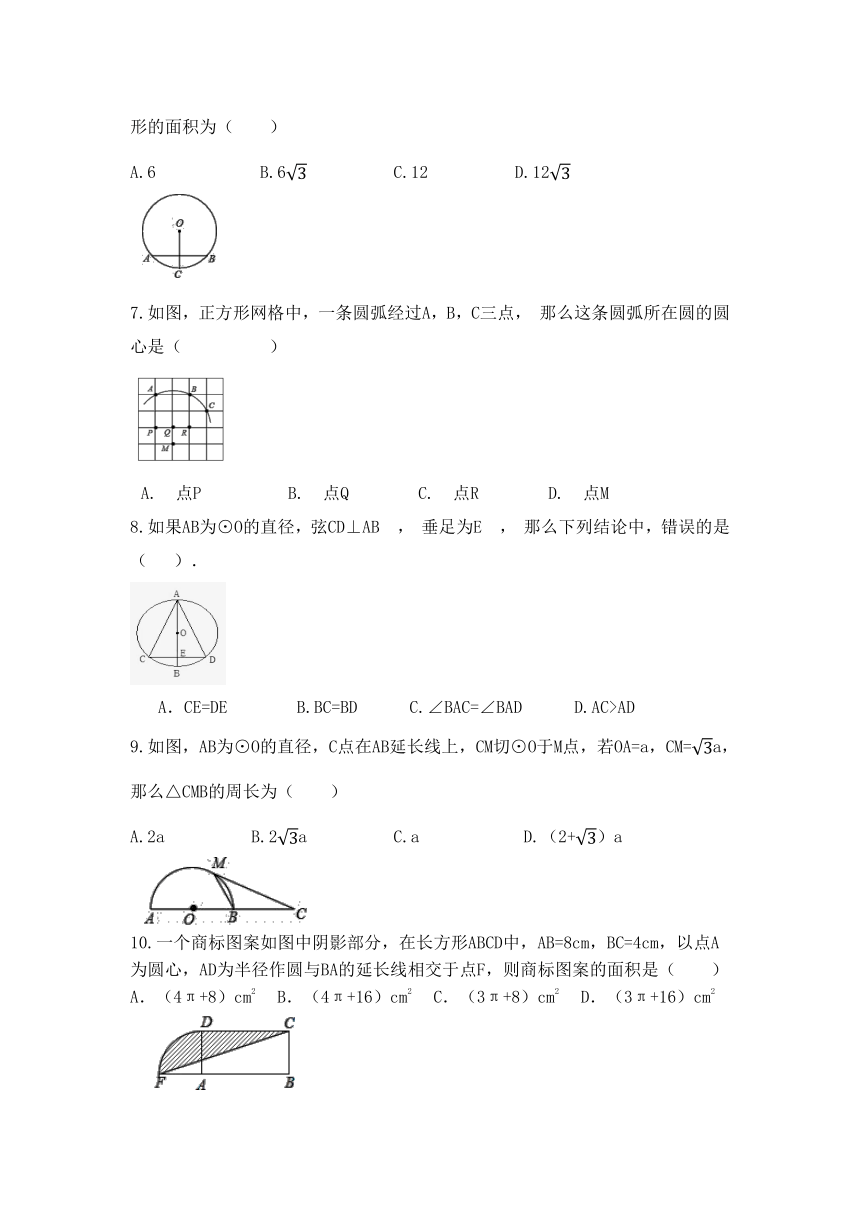

文档简介
第2章
圆
单元测试(3)
选择题
1.如图,已知直线AD是⊙O的切线,A为切点,OD交⊙O于点B,点C在⊙O上,且∠ODA=36°,则∠ACB的度数为( )
A.54°
B.36°
C.30°
D.27°
2.在⊙O中,r=13,弦AB=24,则圆心O到AB的距离为( )
A.?5???B.?10??????C.?12???????D.?13
3.若⊙O内一条弦把圆周分为3∶1的两段弧,且⊙O的半径为R,那么这条弦的长为(
)A.R
B.2R
C.R
D.R
4.如图,正方形ABCD的四个顶点分别在⊙O上,点P在CD上不同于点C的任意一点,则∠BPC的度数是
(???)
A.45°
B.60°
C.75°
D.90°
5.如图,△ABC内接于⊙O,∠OBC=42°,则∠A的度数为( )
A.?84°???B.?96°??????C.?116°??????D.?132°
6.如图,⊙O的一条弦AB垂直平分半径OC,且AB=2,则这个圆的内接正十二边形的面积为( )
A.6??????B.6?????C.12?????D.12
7.如图,正方形网格中,一条圆弧经过A,B,C三点,
那么这条圆弧所在圆的圆心是(?????)
A.?点P?????B.?点Q????C.?点R????D.?点M
8.如果AB为⊙O的直径,弦CD⊥AB
,
垂足为E
,
那么下列结论中,错误的是(?
).
?A.CE=DE
?
??B.BC=BD
?
?C.∠BAC=∠BAD
?
?D.AC>AD
9.如图,AB为⊙O的直径,C点在AB延长线上,CM切⊙O于M点,若OA=a,CM=a,那么△CMB的周长为( )
A.2a?????B.2a?????C.a??????D.(2+)a
10.一个商标图案如图中阴影部分,在长方形ABCD中,AB=8cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积是( )
A.(4π+8)cm2
B.(4π+16)cm2
C.(3π+8)cm2
D.(3π+16)cm2
填空题
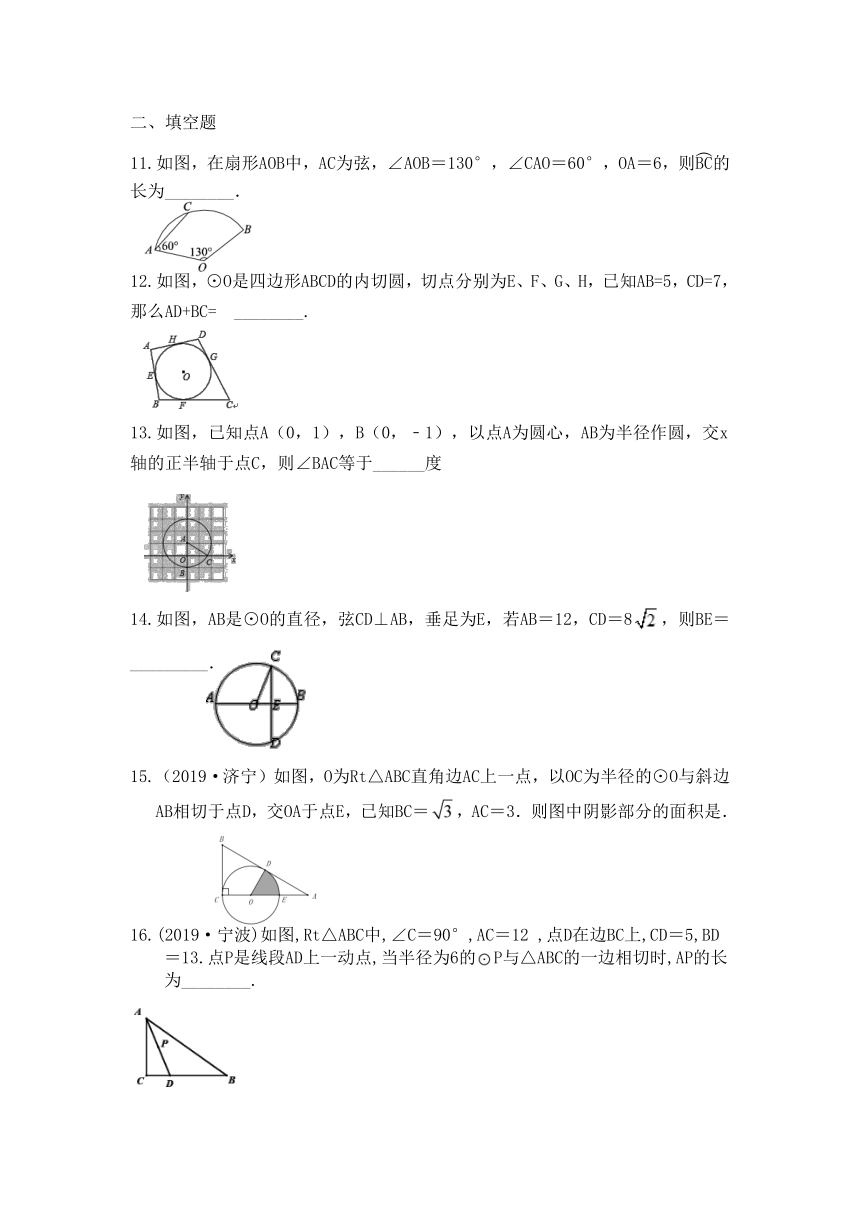
11.如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则的长为________.
12.如图,⊙O是四边形ABCD的内切圆,切点分别为E、F、G、H,已知AB=5,CD=7,那么AD+BC=?________.
?
13.如图,已知点A(0,1),B(0,﹣1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于______度
14.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若AB=12,CD=8,则BE=_________.
15.(2019·济宁)如图,O为Rt△ABC直角边AC上一点,以OC为半径的⊙O与斜边AB相切于点D,交OA于点E,已知BC=,AC=3.则图中阴影部分的面积是.
16.(2019·宁波)如图,Rt△ABC中,∠C=90°,AC=12
,点D在边BC上,CD=5,BD=13.点P是线段AD上一动点,当半径为6的P与△ABC的一边相切时,AP的长为________.
综合题
17.如图,PA,PB是⊙O的切线,A,B为切点,∠APB=60°,连接PO并延长与⊙O交于点C,连接AC,BC.
(1)求证:四边形ACBP是菱形;
(2)若⊙O的半径为1,求菱形ACBP的面积.
18.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线.
(2)过点E作EH⊥AB于点H,求证:CD=HF.
19.(2019浙江省温州市,22,10分)(本题满分10分)
如图,在△ABC中,∠BAC=90°,点E在BC边上,且CA=CE,过A,C,E三点的⊙O交AB于另一点F,作直径AD,连结DE并延长交AB于点G,连结CD,CF.
(1)求证:四边形DCFG是平行四边形;
(2)当BE=4,CD=AB时,求⊙O的直径长.
第2章
圆
单元测试(3)答案
选择题
B
2.A
3.C
4.A
5.D
6.C
7.B
8.
D
9.D
10.A
二、填空题
11.
12.12
13.60
14.4
15.
16.或
三、综合题
17.(1)连接AO,BO,
∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO=12∠APB=30°,
∴∠AOP=60°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠AOP=∠CAO+∠ACO,
∴∠ACO=30°,
∴∠ACO=∠APO,
∴AC=AP,同理BC=PB
∴AC=BC=BP=AP,
∴四边形ACBP是菱形;
(2)连接AB交PC于D,
∴AD⊥PC,
∴OA=1,∠AOP=60°,
∴AD=OA=,
∴PD=,
∴PC=3,AB=,
∴菱形ACBP的面积=AB?PC=
18.证明:(1)如图1,连接OE.
∵BE⊥EF,
∴∠BEF=90°,
∴BF是圆O的直径.
∵BE平分∠ABC,
∴∠CBE=∠OBE,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∴AC是⊙O的切线;
(2)如图2,连结DE.
∵∠CBE=∠OBE,EC⊥BC于C,EH⊥AB于H,
∴EC=EH.
∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,
∴∠CDE=∠HFE.
在△CDE与△HFE中,
,
∴△CDE≌△HFE(AAS),
∴CD=HF.
19.解:(1)连接AE.
∵∠BAC=90°,∴CF是⊙O的直径.
∵
AC=EC,∴CF⊥AE.∵AD为⊙O的直径,
∴∠AED=90°,即GD⊥AE,∴CF∥DG.
∵
AD为⊙O的直径,∴∠ACD=90°,
∴∠ACD+∠BAC=180°,∴AB∥CD,
∴四边形DCFG为平行四边形;
由CD=AB,可设CD=3x,AB=8x,
∴CD=FG=3x.
∵
∠AOF=∠COD,∴AF=CD=3x,∴BG=8x-3x-3x=2x.
∵
GE∥CF,∴△BGE∽△CDE,∴.
又∵
BE=4,∴AC=CE=6,∴BC=6+4=10,∴AB==8=8x,∴x=1.
在Rt△ACF中,AF=3,AC=6,∴CF==3,即⊙O的直径长为3.
圆
单元测试(3)
选择题
1.如图,已知直线AD是⊙O的切线,A为切点,OD交⊙O于点B,点C在⊙O上,且∠ODA=36°,则∠ACB的度数为( )
A.54°
B.36°
C.30°
D.27°
2.在⊙O中,r=13,弦AB=24,则圆心O到AB的距离为( )
A.?5???B.?10??????C.?12???????D.?13
3.若⊙O内一条弦把圆周分为3∶1的两段弧,且⊙O的半径为R,那么这条弦的长为(
)A.R
B.2R
C.R
D.R
4.如图,正方形ABCD的四个顶点分别在⊙O上,点P在CD上不同于点C的任意一点,则∠BPC的度数是
(???)
A.45°
B.60°
C.75°
D.90°
5.如图,△ABC内接于⊙O,∠OBC=42°,则∠A的度数为( )
A.?84°???B.?96°??????C.?116°??????D.?132°
6.如图,⊙O的一条弦AB垂直平分半径OC,且AB=2,则这个圆的内接正十二边形的面积为( )
A.6??????B.6?????C.12?????D.12
7.如图,正方形网格中,一条圆弧经过A,B,C三点,
那么这条圆弧所在圆的圆心是(?????)
A.?点P?????B.?点Q????C.?点R????D.?点M
8.如果AB为⊙O的直径,弦CD⊥AB
,
垂足为E
,
那么下列结论中,错误的是(?
).
?A.CE=DE
?
??B.BC=BD
?
?C.∠BAC=∠BAD
?
?D.AC>AD
9.如图,AB为⊙O的直径,C点在AB延长线上,CM切⊙O于M点,若OA=a,CM=a,那么△CMB的周长为( )
A.2a?????B.2a?????C.a??????D.(2+)a
10.一个商标图案如图中阴影部分,在长方形ABCD中,AB=8cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积是( )
A.(4π+8)cm2
B.(4π+16)cm2
C.(3π+8)cm2
D.(3π+16)cm2
填空题
11.如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则的长为________.
12.如图,⊙O是四边形ABCD的内切圆,切点分别为E、F、G、H,已知AB=5,CD=7,那么AD+BC=?________.
?
13.如图,已知点A(0,1),B(0,﹣1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于______度
14.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若AB=12,CD=8,则BE=_________.
15.(2019·济宁)如图,O为Rt△ABC直角边AC上一点,以OC为半径的⊙O与斜边AB相切于点D,交OA于点E,已知BC=,AC=3.则图中阴影部分的面积是.
16.(2019·宁波)如图,Rt△ABC中,∠C=90°,AC=12
,点D在边BC上,CD=5,BD=13.点P是线段AD上一动点,当半径为6的P与△ABC的一边相切时,AP的长为________.
综合题
17.如图,PA,PB是⊙O的切线,A,B为切点,∠APB=60°,连接PO并延长与⊙O交于点C,连接AC,BC.
(1)求证:四边形ACBP是菱形;
(2)若⊙O的半径为1,求菱形ACBP的面积.
18.如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线.
(2)过点E作EH⊥AB于点H,求证:CD=HF.
19.(2019浙江省温州市,22,10分)(本题满分10分)
如图,在△ABC中,∠BAC=90°,点E在BC边上,且CA=CE,过A,C,E三点的⊙O交AB于另一点F,作直径AD,连结DE并延长交AB于点G,连结CD,CF.
(1)求证:四边形DCFG是平行四边形;
(2)当BE=4,CD=AB时,求⊙O的直径长.
第2章
圆
单元测试(3)答案
选择题
B
2.A
3.C
4.A
5.D
6.C
7.B
8.
D
9.D
10.A
二、填空题
11.
12.12
13.60
14.4
15.
16.或
三、综合题
17.(1)连接AO,BO,
∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO=12∠APB=30°,
∴∠AOP=60°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠AOP=∠CAO+∠ACO,
∴∠ACO=30°,
∴∠ACO=∠APO,
∴AC=AP,同理BC=PB
∴AC=BC=BP=AP,
∴四边形ACBP是菱形;
(2)连接AB交PC于D,
∴AD⊥PC,
∴OA=1,∠AOP=60°,
∴AD=OA=,
∴PD=,
∴PC=3,AB=,
∴菱形ACBP的面积=AB?PC=
18.证明:(1)如图1,连接OE.
∵BE⊥EF,
∴∠BEF=90°,
∴BF是圆O的直径.
∵BE平分∠ABC,
∴∠CBE=∠OBE,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠C=90°,
∴AC是⊙O的切线;
(2)如图2,连结DE.
∵∠CBE=∠OBE,EC⊥BC于C,EH⊥AB于H,
∴EC=EH.
∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,
∴∠CDE=∠HFE.
在△CDE与△HFE中,
,
∴△CDE≌△HFE(AAS),
∴CD=HF.
19.解:(1)连接AE.
∵∠BAC=90°,∴CF是⊙O的直径.
∵
AC=EC,∴CF⊥AE.∵AD为⊙O的直径,
∴∠AED=90°,即GD⊥AE,∴CF∥DG.
∵
AD为⊙O的直径,∴∠ACD=90°,
∴∠ACD+∠BAC=180°,∴AB∥CD,
∴四边形DCFG为平行四边形;
由CD=AB,可设CD=3x,AB=8x,
∴CD=FG=3x.
∵
∠AOF=∠COD,∴AF=CD=3x,∴BG=8x-3x-3x=2x.
∵
GE∥CF,∴△BGE∽△CDE,∴.
又∵
BE=4,∴AC=CE=6,∴BC=6+4=10,∴AB==8=8x,∴x=1.
在Rt△ACF中,AF=3,AC=6,∴CF==3,即⊙O的直径长为3.
