苏科版数学八年级下册 11.2反比例函数图象与性质4——k的几何意义课件 (共20张PPT)
文档属性
| 名称 | 苏科版数学八年级下册 11.2反比例函数图象与性质4——k的几何意义课件 (共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 350.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 21:19:29 | ||
图片预览


文档简介
(共20张PPT)
解析式
图象形状
k>0
位置
增减性
k<0
位置
增减性
双曲线
在一、三象限
每一象限内,y随x的增大而减小。
在二、四象限
反比例函数
每一象限内,y随x的增大而增大。
对称性
延伸趋势
关于原点对称。
无限接近坐标轴但永远没有交点。
复习:
y
x
O
y
x
O
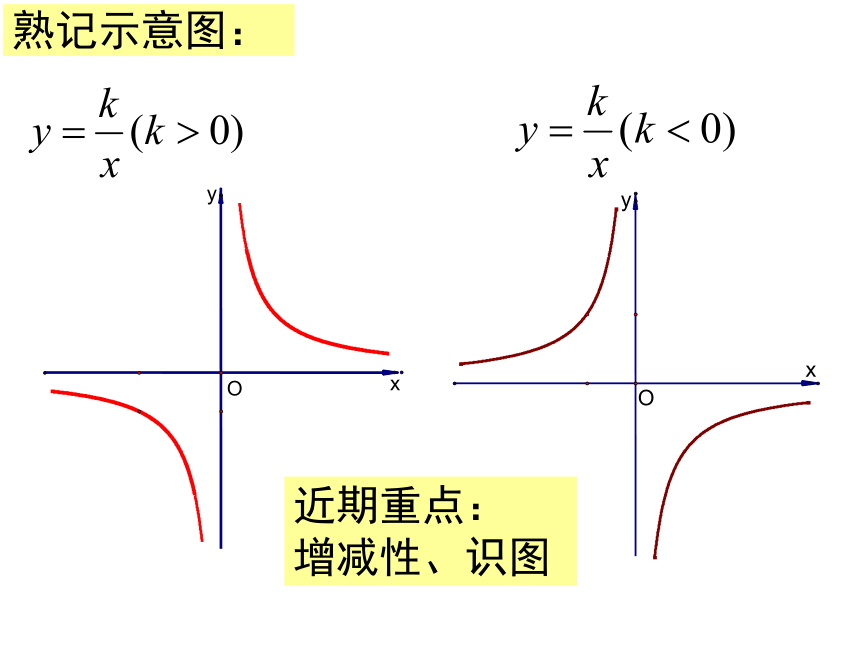
熟记示意图:
近期重点:
增减性、识图
11.2
反比例函数的图像与性质(4)
---k的几何意义
B
A
P(a,b)
y
x
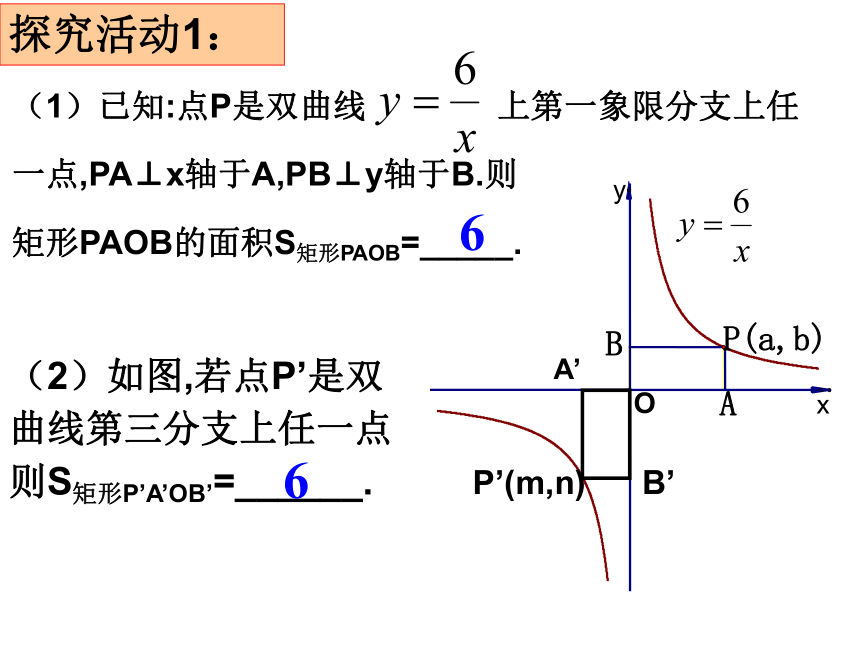
(1)已知:点P是双曲线
上第一象限分支上任
一点,PA⊥x轴于A,PB⊥y轴于B.则
矩形PAOB的面积S矩形PAOB=_____.
(2)如图,若点P’是双曲线第三分支上任一点则S矩形P’A’OB’=______.
P’(m,n)
B’
A’
O
6
6
探究活动1:
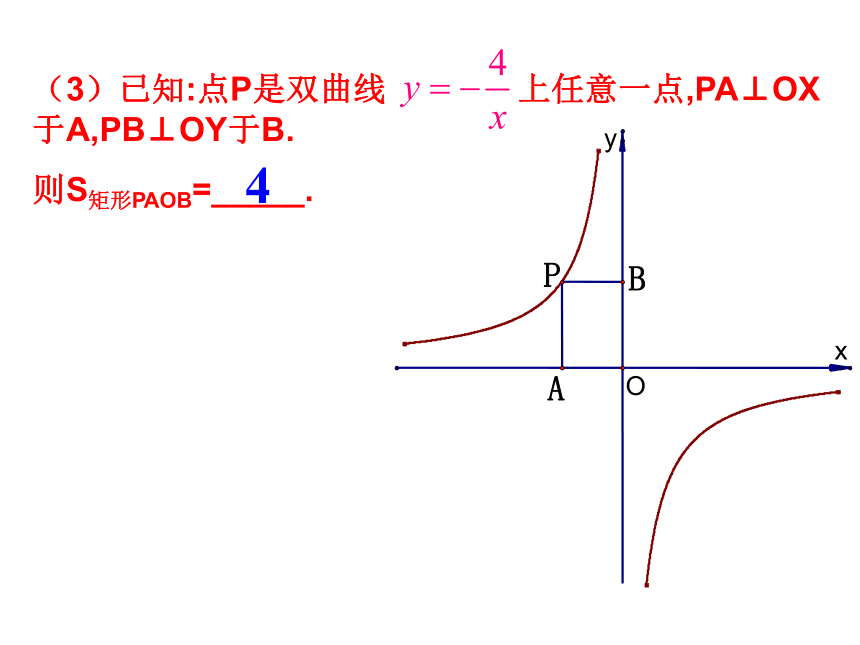
(3)已知:点P是双曲线
上任意一点,PA⊥OX于A,PB⊥OY于B.
则S矩形PAOB=_____.
A
B
y
x
O
P
4
B
A
P(a,b)
y
x
O
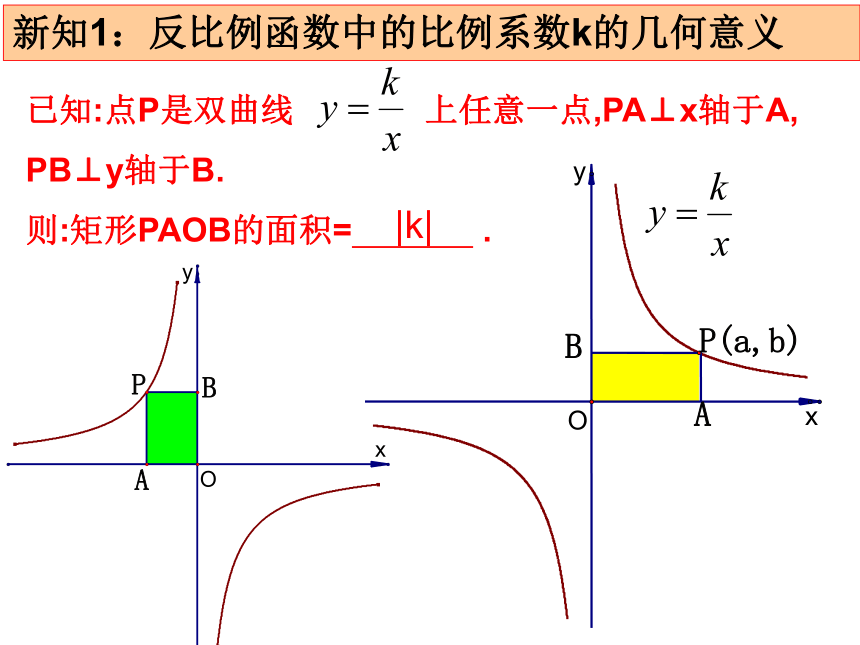
已知:点P是双曲线
上任意一点,PA⊥x轴于A,
PB⊥y轴于B.
则:矩形PAOB的面积=
.
|k|
新知1:反比例函数中的比例系数k的几何意义
y
1
O
A
x
3
图1
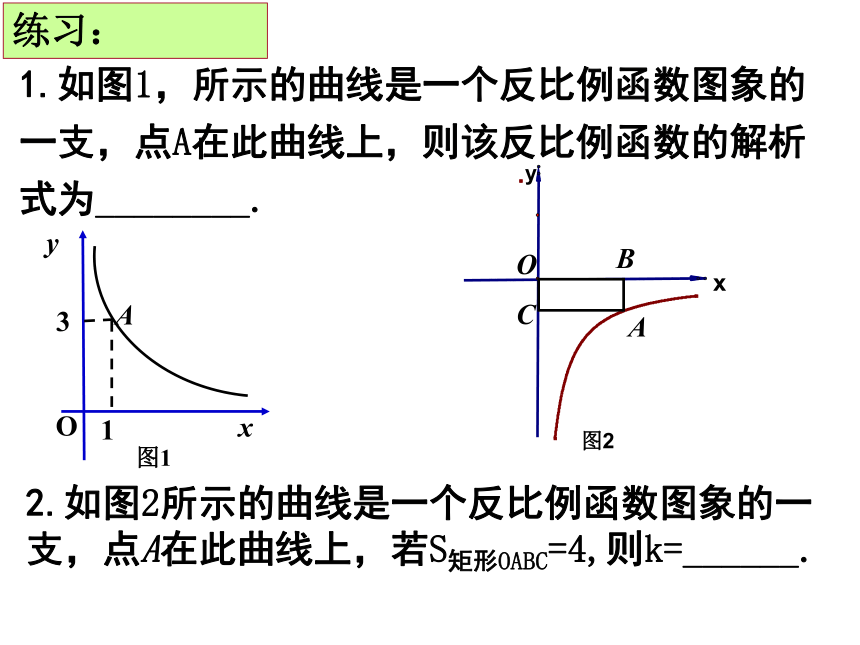
1.如图1,所示的曲线是一个反比例函数图象的一支,点A在此曲线上,则该反比例函数的解析式为________.
x
O
y
A
B
C
O
2.如图2所示的曲线是一个反比例函数图象的一支,点A在此曲线上,若S矩形OABC=4,则k=______.
图2
练习:
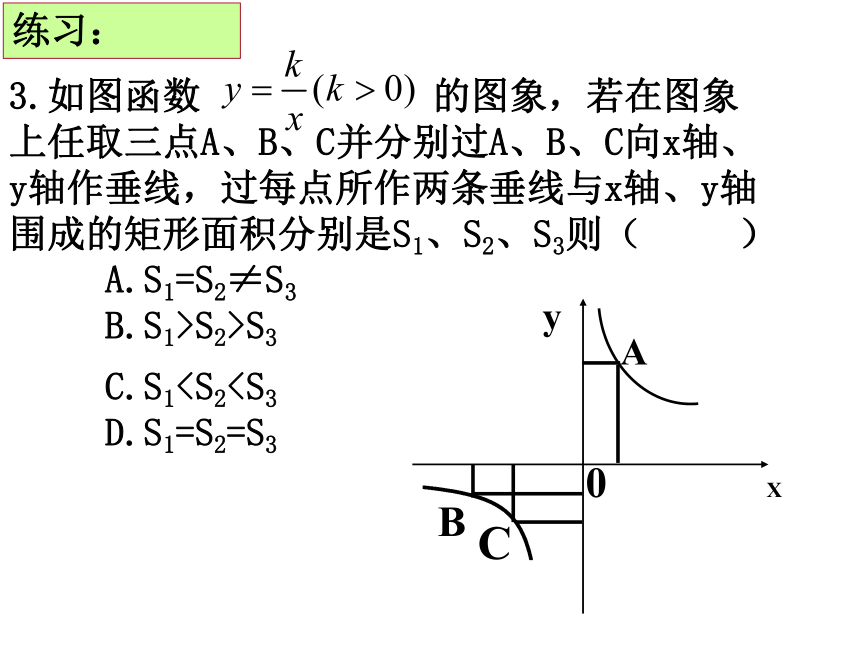
3.如图函数
的图象,若在图象上任取三点A、B、C并分别过A、B、C向x轴、y轴作垂线,过每点所作两条垂线与x轴、y轴围成的矩形面积分别是S1、S2、S3则(
)
A.S1=S2≠S3
B.S1>S2>S3
C.S1D.S1=S2=S3
练习:
B
C
X
y
0
A
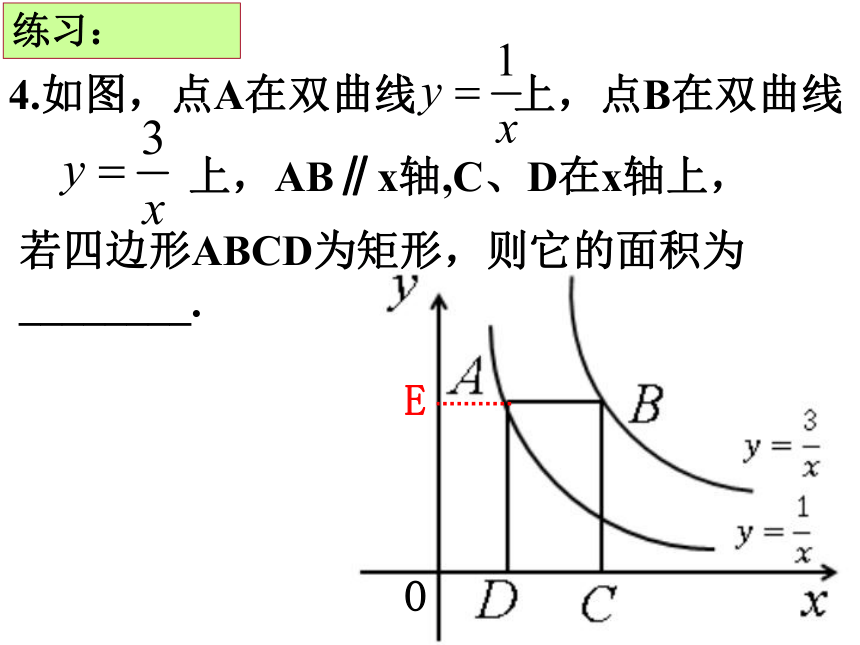
4.如图,点A在双曲线
上,点B在双曲线
上,AB∥x轴,C、D在x轴上,
O
E
若四边形ABCD为矩形,则它的面积为________.
练习:
若点A是双曲线
上任意一点,AB⊥x轴于B,
则△AOB的面积为__________.
|k|
y
o
A(a,b)
B
x
B
O
x
y
A(a,b)
新知2:反比例函数中的比例系数k的几何意义
1、已知如图,A是反比例函数
的图像上的一点,
AB⊥x轴于点B,根据图中信息回答:
y
o
A(a,b)
B
x
B
O
x
y
S
△AOB=____
S
△AOB=____
A(a,b)
练习:
2.(2019无锡)如图,点A为双曲线
(x<0)
的
图像上一点,过点A作AB⊥x轴,垂足为B.若△OAB的面积为2,则k的值为________.
练习:
3.如图,直线
和双曲线
交于A、B两点,
P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别是C、D、E,连接OA、OB、OP,设△AOC面积是S1、△BOD面积是S2、△POE面积是S3
.则(
)
A.
S1<S2<S3
B.
S1>S2>S3
C.
S1=S2>S3
D.
S1=S2练习:
典型例题
例1.已知反比例函数
图像与直线l交于点A(-
2,a),过点A作x轴的垂线,垂足为B,△AOB的面积为3
.
求:k和a
的值;
y
x
O
B
A
l
课堂练习
如图,反比例函数
的图像经过点A(4,b),过点A作AB⊥x轴于点B,△AOB的面积是2.
求k、b的值;
例2.如图,在直角坐标系xOy中,一次函数
y=k1x+b的图象与反比例函数
(x>0)
的图象交于A(1,4)、B(2,m)两点。
(1)求一次函数的解析式;
(2)求△AOB的面积。
O
A(1,4)
B(2,m)
x
y
典型例题
课堂练习
(2019·株洲)如图所示,在直角坐标系xOy中,点A、B、
C为反比例函数
(k>0)上不同的三点,连接OA、OB、
OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF⊥x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3,则(
)
A.S1=S2+S3
B.S1>S2=S3
C.S3>S2>S1
能力提升:
1.(2019·巴中)如图,反比例函数
(x>0)经过A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作BE⊥x轴于点E,连接AD,已知AC=1,BE=1,S矩形BDOE=4,则S△ACD=________.
2.如图:反比例函数
图象上P、Q两
点关于原点成中心对称,且PA⊥x轴于
A,QB⊥x轴于B,连接PB、QA,求四边形
PAQB的面积
P
X
O
Q
A
y
B
能力提升:
谢谢!
解析式
图象形状
k>0
位置
增减性
k<0
位置
增减性
双曲线
在一、三象限
每一象限内,y随x的增大而减小。
在二、四象限
反比例函数
每一象限内,y随x的增大而增大。
对称性
延伸趋势
关于原点对称。
无限接近坐标轴但永远没有交点。
复习:
y
x
O
y
x
O
熟记示意图:
近期重点:
增减性、识图
11.2
反比例函数的图像与性质(4)
---k的几何意义
B
A
P(a,b)
y
x
(1)已知:点P是双曲线
上第一象限分支上任
一点,PA⊥x轴于A,PB⊥y轴于B.则
矩形PAOB的面积S矩形PAOB=_____.
(2)如图,若点P’是双曲线第三分支上任一点则S矩形P’A’OB’=______.
P’(m,n)
B’
A’
O
6
6
探究活动1:
(3)已知:点P是双曲线
上任意一点,PA⊥OX于A,PB⊥OY于B.
则S矩形PAOB=_____.
A
B
y
x
O
P
4
B
A
P(a,b)
y
x
O
已知:点P是双曲线
上任意一点,PA⊥x轴于A,
PB⊥y轴于B.
则:矩形PAOB的面积=
.
|k|
新知1:反比例函数中的比例系数k的几何意义
y
1
O
A
x
3
图1
1.如图1,所示的曲线是一个反比例函数图象的一支,点A在此曲线上,则该反比例函数的解析式为________.
x
O
y
A
B
C
O
2.如图2所示的曲线是一个反比例函数图象的一支,点A在此曲线上,若S矩形OABC=4,则k=______.
图2
练习:
3.如图函数
的图象,若在图象上任取三点A、B、C并分别过A、B、C向x轴、y轴作垂线,过每点所作两条垂线与x轴、y轴围成的矩形面积分别是S1、S2、S3则(
)
A.S1=S2≠S3
B.S1>S2>S3
C.S1
练习:
B
C
X
y
0
A
4.如图,点A在双曲线
上,点B在双曲线
上,AB∥x轴,C、D在x轴上,
O
E
若四边形ABCD为矩形,则它的面积为________.
练习:
若点A是双曲线
上任意一点,AB⊥x轴于B,
则△AOB的面积为__________.
|k|
y
o
A(a,b)
B
x
B
O
x
y
A(a,b)
新知2:反比例函数中的比例系数k的几何意义
1、已知如图,A是反比例函数
的图像上的一点,
AB⊥x轴于点B,根据图中信息回答:
y
o
A(a,b)
B
x
B
O
x
y
S
△AOB=____
S
△AOB=____
A(a,b)
练习:
2.(2019无锡)如图,点A为双曲线
(x<0)
的
图像上一点,过点A作AB⊥x轴,垂足为B.若△OAB的面积为2,则k的值为________.
练习:
3.如图,直线
和双曲线
交于A、B两点,
P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别是C、D、E,连接OA、OB、OP,设△AOC面积是S1、△BOD面积是S2、△POE面积是S3
.则(
)
A.
S1<S2<S3
B.
S1>S2>S3
C.
S1=S2>S3
D.
S1=S2
典型例题
例1.已知反比例函数
图像与直线l交于点A(-
2,a),过点A作x轴的垂线,垂足为B,△AOB的面积为3
.
求:k和a
的值;
y
x
O
B
A
l
课堂练习
如图,反比例函数
的图像经过点A(4,b),过点A作AB⊥x轴于点B,△AOB的面积是2.
求k、b的值;
例2.如图,在直角坐标系xOy中,一次函数
y=k1x+b的图象与反比例函数
(x>0)
的图象交于A(1,4)、B(2,m)两点。
(1)求一次函数的解析式;
(2)求△AOB的面积。
O
A(1,4)
B(2,m)
x
y
典型例题
课堂练习
(2019·株洲)如图所示,在直角坐标系xOy中,点A、B、
C为反比例函数
(k>0)上不同的三点,连接OA、OB、
OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF⊥x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3,则(
)
A.S1=S2+S3
B.S1>S2=S3
C.S3>S2>S1
能力提升:
1.(2019·巴中)如图,反比例函数
(x>0)经过A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作BE⊥x轴于点E,连接AD,已知AC=1,BE=1,S矩形BDOE=4,则S△ACD=________.
2.如图:反比例函数
图象上P、Q两
点关于原点成中心对称,且PA⊥x轴于
A,QB⊥x轴于B,连接PB、QA,求四边形
PAQB的面积
P
X
O
Q
A
y
B
能力提升:
谢谢!
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
