河南省郑州枫杨外国语学校2019-2020学年下期开学测试九年级数学试题(无答案)
文档属性
| 名称 | 河南省郑州枫杨外国语学校2019-2020学年下期开学测试九年级数学试题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 235.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 08:10:03 | ||
图片预览



文档简介
2019-2020学年下期开学测试九年级数学试题
一、选择题(每题3分,共30分)
1.
下列实数中,是无理数的是( )
B.3.14
C.
D.
天文单位是天文学中计量天体之间距离的一种单位,其数值取地球与太阳之间的平均距离,即149597870700m,约为149600000km.将数149600000用科学记数法表示为( )
A.
14.96×107
B.1.496×107
C.14.96×108
D.1.496×108
3.
下列计算正确的是( )
A.(a4b)3=a7b3
B.﹣2b(4a﹣b2)=﹣8ab﹣2b3
C.aa3+a2a2=2a4
D.(a﹣5)2=a2﹣25
4.
如图是一个零件的示意图,它的俯视图是( )
A.
B.
C.
D.
5.
疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表所示,则他们捐款金额的平均数和中位数分别是(
)
金额/元
5
10
20
50
100
人数
6
17
14
8
5
A.27.6,10
B.27.6,20
C.37,10
D.37,20
6.
在四川抗震救灾中,某抢险地段需实行爆破.操作人员点燃导火线后,要在炸药爆炸前跑到450米以外的安全区域.已知导火线的燃烧速度是1.3厘米/秒,操作人员跑步的速度是5米/秒.为了保证操作人员的安全,导火线的长度要超过(
)
A.87厘米
B.97厘米
C.107厘米
D.117厘米
7.
若不等式解集中x的每一个值,都能使得关于x的不等式成立,则m的取值范围是(
)
A.
B.
C.
D.
8
如图,小明在以∠A为顶角的等腰三角形ABC中用圆规和直尺作图,作出过点A的射线交BC于点D,然后又作出一条直线与AB交于点E,连接DE,若△ABC的面积为4,则△BED的面积为( )
A.1
B.2
C.3
D.4
第8题图
第9题图
第10题图
9.
2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军.如图是某次比赛中垫球时的动作.若将垫球后排球的运动路线近似的看作抛物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点A)离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点B)越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点C)距球网的水平距离为2.5米,则排球运动路线的函数表达式为(
)
A.
B.
C.
D.
10.
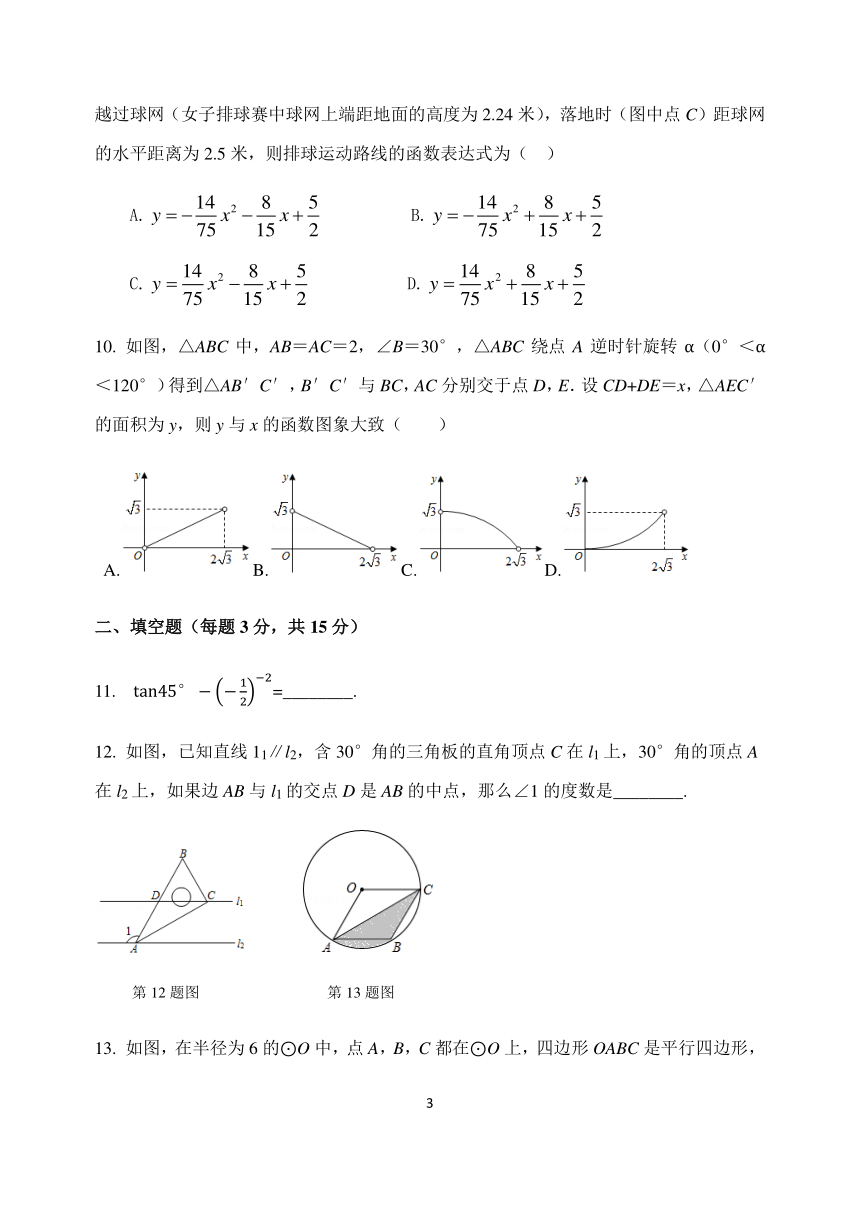
如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0°<α<120°)得到△AB′C′,B′C′与BC,AC分别交于点D,E.设CD+DE=x,△AEC′的面积为y,则y与x的函数图象大致( )
A.B.C.D.
二、填空题(每题3分,共15分)
11.
=________.
12.
如图,已知直线11∥l2,含30°角的三角板的直角顶点C在l1上,30°角的顶点A在l2上,如果边AB与l1的交点D是AB的中点,那么∠1的度数是________.
第12题图
第13题图
13.
如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为 _____.
14.
关于x的方程﹣1=的解为非负数,则k的取值范围是 _____.
15.
在矩形ABCD中,AB=5,AD=4,点E是射线AD上的一个动点,把△BAE沿BE折叠,点A对应点A′落在射线DC上,则AE的长为 _____.
三、解答题(共75分)
16.
(8分)先化简÷(﹣x﹣2),然后请你选择一个合适的数作为x的值代入求值.
17.
(9分)某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下::
4.2
4.1
4.7
4.1
4.3
4.3
4.4
4.6
4.1
5.2
5.2
4.5
5.0
4.5
4.3
4.4
4.8
5.3
4.5
5.2
4.4
4.2
4.3
5.3
4.9
5.2
4.9
4.8
4.6
5.1
4.2
4.4
4.5
4.1
4.5
5.1
4.4
5.0
5.2
5.3
根据数据绘制了如图的表格和统计图:
等级
视力(x)
频数
频率
A
x<4.2
4
0.1
B
4.2≤x≤4.4
12
0.3
C
4.5≤x≤4.7
a
D
4.8≤x≤5.0
b
E
5.1≤x≤5.3
10
0.25
合计
40
1
根据上面提供的信息,回答下列问题:
(1)统计表中的a= ,b= ;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“D级”的有多少人?
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
18.(9分)
如图,AB是⊙O的直径,C,G是⊙O上两点,且=,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线;
(2)当AE=AO时,
①则的值为________;②若CD=,则AD=___________.
(9分)如图,过点C(3,4)的直线y=2x+b交x轴于点A,∠ABC=90°,AB=CB,双曲线y=(x>0)过点B.
(1)求双曲线的解析式;
(2)将△ABC沿x轴正方向平移a(a>0)个单位长度,恰好使得一边的中点落在该曲线上,求a的值.
20.
(9分)有一种落地晾衣架如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度.图2是支撑杆的平面示意图,AB和CD分别是两根不同长度的支撑杆,夹角∠BOD=α.若AO=85cm,BO=DO=65cm.问:当α=74°时,较长支撑杆的端点A离地面的高度h约为多少cm?(结果保留整数.参考数据:sin37°≈0.60,cos37°≈0.80,sin74°≈0.96,cos74°≈0.27.)
21.(10分)近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加,某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见表:
A型销售数量(台)
B型销售数量(台)
总利润(元)
5
3
950
3
2
600
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共80台,其中B型空气净化器的进货量不多于A型空气净化器的2倍,为使该公司销售完这80台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为200
m3/小时,B型空气净化器的净化能力为280
m3/小时,某长方体室内活动场地的总面积为200
m2,室内墙高3
m,该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,若不考虑空气对流等因素,至多要购买A型空气净化器多少台?
22.(10分)如图①,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点D,E,N分别是△ABC的AB,AC,BC边上的中点,连接AN,DE交于点M.
(1)观察猜想:
的值为 ;BD与CE的位置关系是_________.
(2)探究与证明:
将△ADE绕点A按顺时针方向旋转α角(0°<α<360°),且△ADE内部的线段AM随之旋转,如图②所示,连接BD,CE,MN,试探究线段BD与MN之间分别有什么样的数量关系,以及BD与CE有什么样的位置关系,并证明;
(3)拓展与延伸:
△ADE在旋转的过程中,设直线CE与BD相交于点F,当∠CAE=90°时,请直接写出BF的值.
23.
(11分)如图,已知:抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,点D为顶点,连接BD,CD,抛物线的对称轴与x轴交与点
E.
(1)求抛物线解析式及点D的坐标;
(2)G是抛物线上B,D之间的一点,且S四边形CDGB=4S△DGB,求出G点坐标;
(3)在抛物线上B,D之间是否存在一点M,过点M作MN⊥CD,交直线CD于点N,使以C,M,N为顶点的三角形与△BDE相似?若存在,求出满足条件的点M的坐标,若不存在,请说明理由.
(
6
)
一、选择题(每题3分,共30分)
1.
下列实数中,是无理数的是( )
B.3.14
C.
D.
天文单位是天文学中计量天体之间距离的一种单位,其数值取地球与太阳之间的平均距离,即149597870700m,约为149600000km.将数149600000用科学记数法表示为( )
A.
14.96×107
B.1.496×107
C.14.96×108
D.1.496×108
3.
下列计算正确的是( )
A.(a4b)3=a7b3
B.﹣2b(4a﹣b2)=﹣8ab﹣2b3
C.aa3+a2a2=2a4
D.(a﹣5)2=a2﹣25
4.
如图是一个零件的示意图,它的俯视图是( )
A.
B.
C.
D.
5.
疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表所示,则他们捐款金额的平均数和中位数分别是(
)
金额/元
5
10
20
50
100
人数
6
17
14
8
5
A.27.6,10
B.27.6,20
C.37,10
D.37,20
6.
在四川抗震救灾中,某抢险地段需实行爆破.操作人员点燃导火线后,要在炸药爆炸前跑到450米以外的安全区域.已知导火线的燃烧速度是1.3厘米/秒,操作人员跑步的速度是5米/秒.为了保证操作人员的安全,导火线的长度要超过(
)
A.87厘米
B.97厘米
C.107厘米
D.117厘米
7.
若不等式解集中x的每一个值,都能使得关于x的不等式成立,则m的取值范围是(
)
A.
B.
C.
D.
8
如图,小明在以∠A为顶角的等腰三角形ABC中用圆规和直尺作图,作出过点A的射线交BC于点D,然后又作出一条直线与AB交于点E,连接DE,若△ABC的面积为4,则△BED的面积为( )
A.1
B.2
C.3
D.4
第8题图
第9题图
第10题图
9.
2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军.如图是某次比赛中垫球时的动作.若将垫球后排球的运动路线近似的看作抛物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点A)离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点B)越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点C)距球网的水平距离为2.5米,则排球运动路线的函数表达式为(
)
A.
B.
C.
D.
10.
如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0°<α<120°)得到△AB′C′,B′C′与BC,AC分别交于点D,E.设CD+DE=x,△AEC′的面积为y,则y与x的函数图象大致( )
A.B.C.D.
二、填空题(每题3分,共15分)
11.
=________.
12.
如图,已知直线11∥l2,含30°角的三角板的直角顶点C在l1上,30°角的顶点A在l2上,如果边AB与l1的交点D是AB的中点,那么∠1的度数是________.
第12题图
第13题图
13.
如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为 _____.
14.
关于x的方程﹣1=的解为非负数,则k的取值范围是 _____.
15.
在矩形ABCD中,AB=5,AD=4,点E是射线AD上的一个动点,把△BAE沿BE折叠,点A对应点A′落在射线DC上,则AE的长为 _____.
三、解答题(共75分)
16.
(8分)先化简÷(﹣x﹣2),然后请你选择一个合适的数作为x的值代入求值.
17.
(9分)某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下::
4.2
4.1
4.7
4.1
4.3
4.3
4.4
4.6
4.1
5.2
5.2
4.5
5.0
4.5
4.3
4.4
4.8
5.3
4.5
5.2
4.4
4.2
4.3
5.3
4.9
5.2
4.9
4.8
4.6
5.1
4.2
4.4
4.5
4.1
4.5
5.1
4.4
5.0
5.2
5.3
根据数据绘制了如图的表格和统计图:
等级
视力(x)
频数
频率
A
x<4.2
4
0.1
B
4.2≤x≤4.4
12
0.3
C
4.5≤x≤4.7
a
D
4.8≤x≤5.0
b
E
5.1≤x≤5.3
10
0.25
合计
40
1
根据上面提供的信息,回答下列问题:
(1)统计表中的a= ,b= ;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“D级”的有多少人?
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
18.(9分)
如图,AB是⊙O的直径,C,G是⊙O上两点,且=,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线;
(2)当AE=AO时,
①则的值为________;②若CD=,则AD=___________.
(9分)如图,过点C(3,4)的直线y=2x+b交x轴于点A,∠ABC=90°,AB=CB,双曲线y=(x>0)过点B.
(1)求双曲线的解析式;
(2)将△ABC沿x轴正方向平移a(a>0)个单位长度,恰好使得一边的中点落在该曲线上,求a的值.
20.
(9分)有一种落地晾衣架如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度.图2是支撑杆的平面示意图,AB和CD分别是两根不同长度的支撑杆,夹角∠BOD=α.若AO=85cm,BO=DO=65cm.问:当α=74°时,较长支撑杆的端点A离地面的高度h约为多少cm?(结果保留整数.参考数据:sin37°≈0.60,cos37°≈0.80,sin74°≈0.96,cos74°≈0.27.)
21.(10分)近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加,某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见表:
A型销售数量(台)
B型销售数量(台)
总利润(元)
5
3
950
3
2
600
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共80台,其中B型空气净化器的进货量不多于A型空气净化器的2倍,为使该公司销售完这80台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为200
m3/小时,B型空气净化器的净化能力为280
m3/小时,某长方体室内活动场地的总面积为200
m2,室内墙高3
m,该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,若不考虑空气对流等因素,至多要购买A型空气净化器多少台?
22.(10分)如图①,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点D,E,N分别是△ABC的AB,AC,BC边上的中点,连接AN,DE交于点M.
(1)观察猜想:
的值为 ;BD与CE的位置关系是_________.
(2)探究与证明:
将△ADE绕点A按顺时针方向旋转α角(0°<α<360°),且△ADE内部的线段AM随之旋转,如图②所示,连接BD,CE,MN,试探究线段BD与MN之间分别有什么样的数量关系,以及BD与CE有什么样的位置关系,并证明;
(3)拓展与延伸:
△ADE在旋转的过程中,设直线CE与BD相交于点F,当∠CAE=90°时,请直接写出BF的值.
23.
(11分)如图,已知:抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,点D为顶点,连接BD,CD,抛物线的对称轴与x轴交与点
E.
(1)求抛物线解析式及点D的坐标;
(2)G是抛物线上B,D之间的一点,且S四边形CDGB=4S△DGB,求出G点坐标;
(3)在抛物线上B,D之间是否存在一点M,过点M作MN⊥CD,交直线CD于点N,使以C,M,N为顶点的三角形与△BDE相似?若存在,求出满足条件的点M的坐标,若不存在,请说明理由.
(
6
)
同课章节目录
