沪教版高中数学高二下册12.2 圆的标准方程 课件(共20张PPT)
文档属性
| 名称 | 沪教版高中数学高二下册12.2 圆的标准方程 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 09:24:35 | ||
图片预览






文档简介
(共20张PPT)
圆的标准方程
奥运五环
福建土楼
河北赵州桥
车轮
圆的定义
平面内到一个定点的距离等于定长(大于零)的点的轨迹就是圆。
圆心
半径
o
y
x
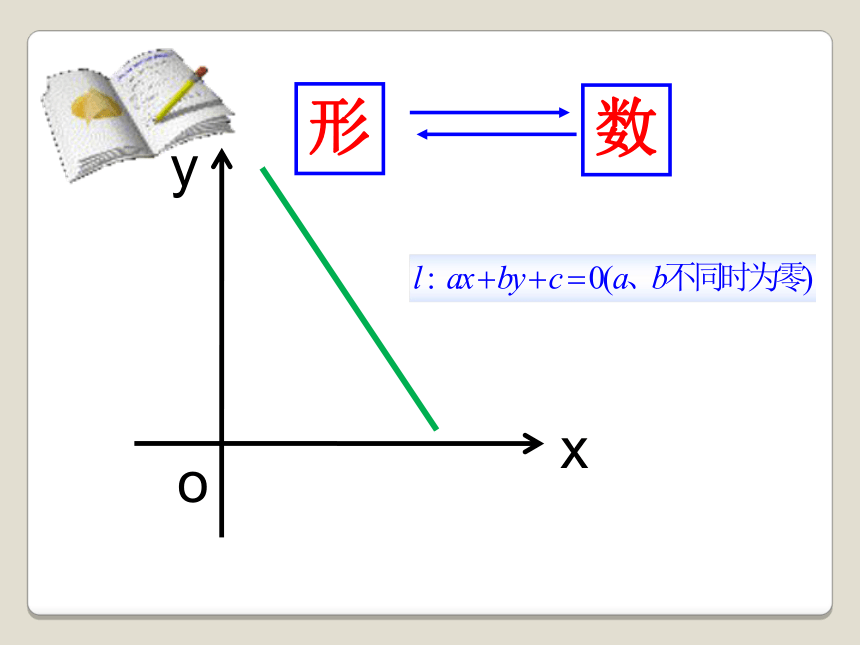
形
数
O
y
x
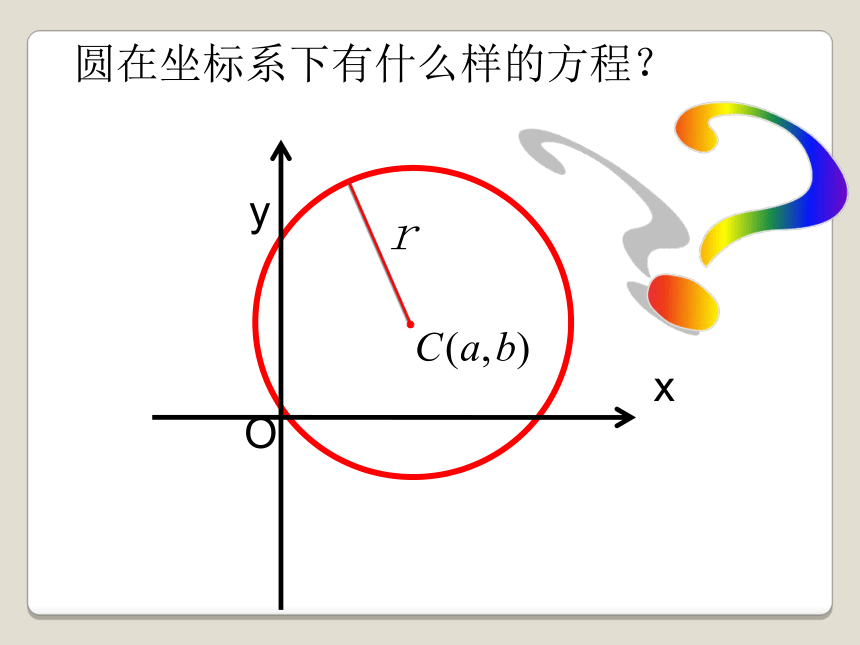
圆在坐标系下有什么样的方程?
建系设点
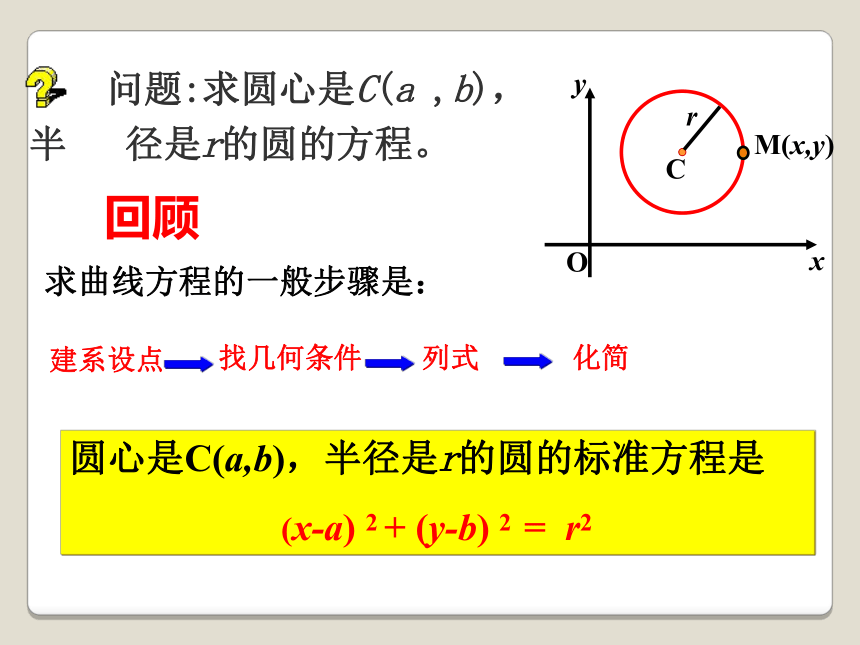
圆心是C(a,b),半径是r的圆的标准方程是
(x-a)
2
+
(y-b)
2
=
r2
找几何条件
列式
化简
C
M(x,y)
r
问题:求圆心是C(a
,b),半
径是r的圆的方程。
求曲线方程的一般步骤是:
回顾
突出了圆的几何特点;
方程明确给出了圆心坐标和半径;
记忆:
圆的标准方程有哪些特点?
圆心是C(a,b),半径是r的圆的标准方程是
(x-a)
2
+
(y-b)
2
=
r2
口答练习1:
说出下列圆的标准方程:
(1)圆心在原点,半径为3;
(2)圆心在(3,-4),半径为7;
(3)圆心在(3,2),且与
y轴相切;
口答练习1:
说出下列圆的标准方程:
(1)圆心在原点,半径为3;
(2)圆心在(3,-4),半径为7;
(3)圆心在(3,2),且与
x轴相切;
口答练习2:说出下列圆的圆心坐标和半径:
也可用两点间距离公式求r
(精确到0.01m)
如图是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20m,
拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度(精确到0.01m)
x
y
练习2:
如图是某圆拱桥的一孔圆拱的示意图。该圆拱跨度AB=20
m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度(精确到0.01m)
则圆的方程是
x
2+(
y
-b)2
=r
2。
解:建立坐标系如图所示,
圆心在y轴上。
设圆心坐标是(0,b),
圆的半径是r
,
因为P、B都在圆上,所以它们的坐标(0,4)、(10,0)都是圆的方程的解。所以有
解之得:b
=
-10.5
,
r2=14.5
2
把点P2的横坐标x
=
-2
代入圆的方程,得
(-2)
2
+
(y
+
10.5)
2
=
14.5
2
因为P
2
的纵坐标
y
>
0
,所以
≈14.36
-10.5
=
3.86(m)
答:支柱A2P2的长度约为3.86m。
(续)
所以圆的方程是:
x2
+
(y
+
10.5)
2
=
14.5
2
如图是某圆拱桥的一孔圆拱的示意图。该圆拱跨度AB=20
m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度(精确到0.01m)
小结
以C(a,b)为圆心,
r?0为半径的圆的方程为:
称上述形式的圆的方程为圆的标准方程.
特别地:
以原点为圆心,
r?0为半径的圆的标准方程是
方法:定圆心,求半径
圆的标准方程
奥运五环
福建土楼
河北赵州桥
车轮
圆的定义
平面内到一个定点的距离等于定长(大于零)的点的轨迹就是圆。
圆心
半径
o
y
x
形
数
O
y
x
圆在坐标系下有什么样的方程?
建系设点
圆心是C(a,b),半径是r的圆的标准方程是
(x-a)
2
+
(y-b)
2
=
r2
找几何条件
列式
化简
C
M(x,y)
r
问题:求圆心是C(a
,b),半
径是r的圆的方程。
求曲线方程的一般步骤是:
回顾
突出了圆的几何特点;
方程明确给出了圆心坐标和半径;
记忆:
圆的标准方程有哪些特点?
圆心是C(a,b),半径是r的圆的标准方程是
(x-a)
2
+
(y-b)
2
=
r2
口答练习1:
说出下列圆的标准方程:
(1)圆心在原点,半径为3;
(2)圆心在(3,-4),半径为7;
(3)圆心在(3,2),且与
y轴相切;
口答练习1:
说出下列圆的标准方程:
(1)圆心在原点,半径为3;
(2)圆心在(3,-4),半径为7;
(3)圆心在(3,2),且与
x轴相切;
口答练习2:说出下列圆的圆心坐标和半径:
也可用两点间距离公式求r
(精确到0.01m)
如图是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20m,
拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度(精确到0.01m)
x
y
练习2:
如图是某圆拱桥的一孔圆拱的示意图。该圆拱跨度AB=20
m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度(精确到0.01m)
则圆的方程是
x
2+(
y
-b)2
=r
2。
解:建立坐标系如图所示,
圆心在y轴上。
设圆心坐标是(0,b),
圆的半径是r
,
因为P、B都在圆上,所以它们的坐标(0,4)、(10,0)都是圆的方程的解。所以有
解之得:b
=
-10.5
,
r2=14.5
2
把点P2的横坐标x
=
-2
代入圆的方程,得
(-2)
2
+
(y
+
10.5)
2
=
14.5
2
因为P
2
的纵坐标
y
>
0
,所以
≈14.36
-10.5
=
3.86(m)
答:支柱A2P2的长度约为3.86m。
(续)
所以圆的方程是:
x2
+
(y
+
10.5)
2
=
14.5
2
如图是某圆拱桥的一孔圆拱的示意图。该圆拱跨度AB=20
m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度(精确到0.01m)
小结
以C(a,b)为圆心,
r?0为半径的圆的方程为:
称上述形式的圆的方程为圆的标准方程.
特别地:
以原点为圆心,
r?0为半径的圆的标准方程是
方法:定圆心,求半径
