人教版八年级数学下册第十六章《二次根式》练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册第十六章《二次根式》练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 131.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 12:29:08 | ||
图片预览


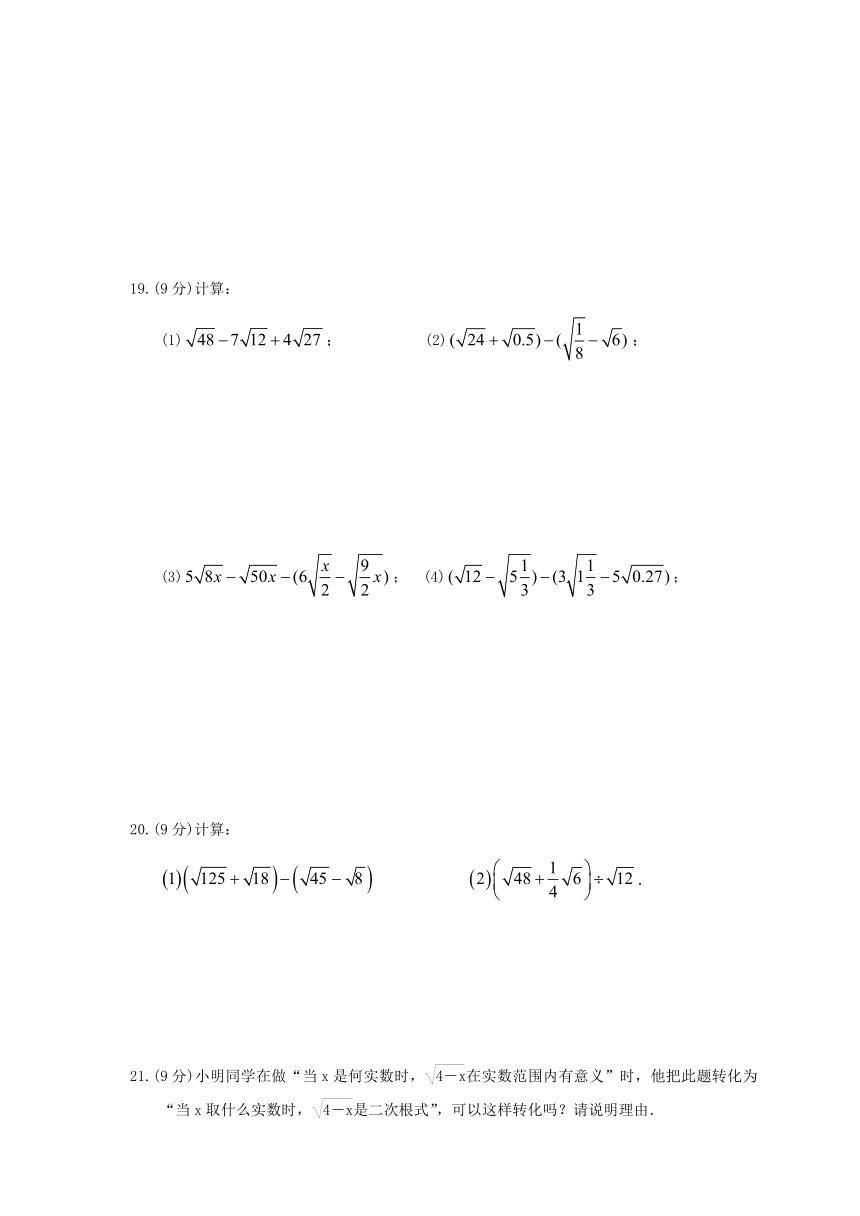
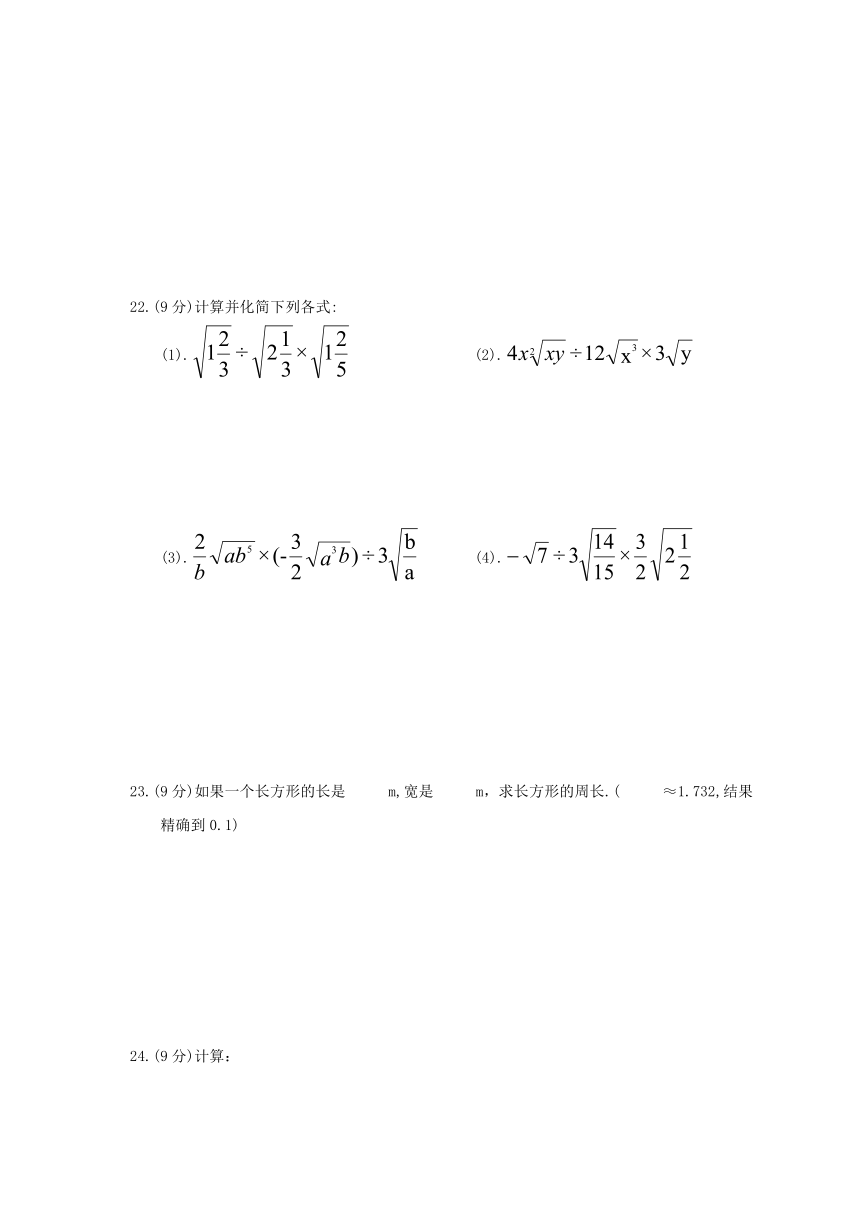
文档简介
八年级数学下册
第十六章《二次根式》练习
姓名:__________班级:__________考号:__________
一、选择题(本大题共10小题,每小题3分,共30分)
1.下面与是同类二次根式的是(
)
A.
B.
C.
D.
2.如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为(
)cm2.
A.16﹣8
B.﹣12+8
C.8﹣4
D.4﹣2
3.式子有意义的x的取值范围是(
)
A.x≥﹣且x≠1
B.x≠1
C.
D.x>﹣且x≠1
4.若a>0,则的值为(
)
A.1
B.﹣1
C.±1
D.﹣a
5.下列各式计算正确的是(
)
A.=2
B.÷=
C.()2=3
D.=﹣2
6.计算
+3
-
-
,得(
)
A.1
B.0
C.
D.8
7.下列计算正确的是(
)
A.2
+3
=5
B.(
+1)(1-
)=1
C.-(-
a
)
4
÷
a
2
=
a
2
D.(
xy
)
-
1
(
xy
)
2
=
xy
8.若与-互为倒数,则(
)
A.
a=b-1
B.
a=b+1
C.
a+b=1
D.
a+b=-1
9.按如图所示的程序计算,若开始输入的n值为,则最后输出的结果是(
)
A.14
B.16
C.8+5
D.14+
10.下列各数中,与2的积为有理数的是()
A.2
B.3
C.
二、填空题(本大题共6小题,每小题3分,共18分)
11.若整数m满足条件=m+1且m<,则m的值是____________.
12.(2019年江苏徐州)若有意义的x的取值范围是_________.
13.若成立,则x满足_______________
14.已知实数a、b在数轴上的位置如图所示,则化简的结果为________
15.若最简二次根式与可以合并,则a的值为________.
16.二次根式的加减法法则:一般地,二次根式加减时,可以先将二次根式化成________,再将________相同的二次根式进行合并.
三、解答题(本大题共8小题,共72分)
17.(9分)如果的整数部分是a,小数部分是b求的值。
18.(9分)一个三角形一边长为cm,这边长的高是cm,求这个三角形的面积
19.(9分)计算:
(1);
(2);
(3);
(4);
20.(9分)计算:
.
21.(9分)小明同学在做“当x是何实数时,在实数范围内有意义”时,他把此题转化为“当x取什么实数时,是二次根式”,可以这样转化吗?请说明理由.
22.(9分)计算并化简下列各式:
(1).
(2).
(3).
(4).
23.(9分)如果一个长方形的长是
m,宽是
m,求长方形的周长.(
≈1.732,结果精确到0.1)
24.(9分)计算:
(1)
(2)(4﹣3)×.
(3)
(4)
(5)
答案解析
1.C
2.B解:∵两张正方形纸片的面积分别为16cm2和12cm2,
∴它们的边长分别为=4cm,
=2cm,
∴AB=4cm,BC=(2+4)cm,
∴空白部分的面积=(2+4)×4﹣12﹣16,
=8+16﹣12﹣16,
=(﹣12+8)cm2.
3.A
4.B【解答】解:∵a>0,∴=a.
==﹣1.
5.C解:A.==,此选项错误;
B.÷==,此选项错误;
C.()2=3,此选项正确;
D.=2,此选项错误;
6.B
7.D
8.D
9.C【分析】根据给出的运算程序计算即可.
【解答】解:当n=时,n(n+1)=2+<15,
当n=2+时,n(n+1)=8+5>15,
【点评】本题考查的是二次根式的混合运算,掌握二次根式的混合运算法则是解题的关键.
10.D
11.0或-1
12.x≥-1
{解析}本题考查了分式有意义的条件,根据题意有:x+1≥0,∴x≥-1.
13.解:由题意,3-x>0,x-2≧0,所以2≦x<3.
14.0【解析】由图可知:a<0,b>0,
b-a>0,
∴
故填:0
15.4点拨:∵最简二次根式与可以合并,∴它们的被开方数相同,即3a-1=2a+3,解得a=4.
16.最简二次根式
被开方数
17.解:,
.
18.
19.(1)
(2)
(3)
(4)
20.(1);(2)2+
21.解:可以.
理由:第一个问题的解答是根据二次根式的定义,得出被开方数大于或等于0,从而求出x的取值范围;而第二个问题的解答也是根据二次根式的定义,得出被开方数大于或等于0,进而得出x的取值范围,这两题考查的知识及解答方法完全一样,所以可以如此转化.
22.(1)1;(2)xy
23.17.3
m.
24.(1);(2)16﹣12;(3);(4)20+6;(5)5+
第十六章《二次根式》练习
姓名:__________班级:__________考号:__________
一、选择题(本大题共10小题,每小题3分,共30分)
1.下面与是同类二次根式的是(
)
A.
B.
C.
D.
2.如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为(
)cm2.
A.16﹣8
B.﹣12+8
C.8﹣4
D.4﹣2
3.式子有意义的x的取值范围是(
)
A.x≥﹣且x≠1
B.x≠1
C.
D.x>﹣且x≠1
4.若a>0,则的值为(
)
A.1
B.﹣1
C.±1
D.﹣a
5.下列各式计算正确的是(
)
A.=2
B.÷=
C.()2=3
D.=﹣2
6.计算
+3
-
-
,得(
)
A.1
B.0
C.
D.8
7.下列计算正确的是(
)
A.2
+3
=5
B.(
+1)(1-
)=1
C.-(-
a
)
4
÷
a
2
=
a
2
D.(
xy
)
-
1
(
xy
)
2
=
xy
8.若与-互为倒数,则(
)
A.
a=b-1
B.
a=b+1
C.
a+b=1
D.
a+b=-1
9.按如图所示的程序计算,若开始输入的n值为,则最后输出的结果是(
)
A.14
B.16
C.8+5
D.14+
10.下列各数中,与2的积为有理数的是()
A.2
B.3
C.
二、填空题(本大题共6小题,每小题3分,共18分)
11.若整数m满足条件=m+1且m<,则m的值是____________.
12.(2019年江苏徐州)若有意义的x的取值范围是_________.
13.若成立,则x满足_______________
14.已知实数a、b在数轴上的位置如图所示,则化简的结果为________
15.若最简二次根式与可以合并,则a的值为________.
16.二次根式的加减法法则:一般地,二次根式加减时,可以先将二次根式化成________,再将________相同的二次根式进行合并.
三、解答题(本大题共8小题,共72分)
17.(9分)如果的整数部分是a,小数部分是b求的值。
18.(9分)一个三角形一边长为cm,这边长的高是cm,求这个三角形的面积
19.(9分)计算:
(1);
(2);
(3);
(4);
20.(9分)计算:
.
21.(9分)小明同学在做“当x是何实数时,在实数范围内有意义”时,他把此题转化为“当x取什么实数时,是二次根式”,可以这样转化吗?请说明理由.
22.(9分)计算并化简下列各式:
(1).
(2).
(3).
(4).
23.(9分)如果一个长方形的长是
m,宽是
m,求长方形的周长.(
≈1.732,结果精确到0.1)
24.(9分)计算:
(1)
(2)(4﹣3)×.
(3)
(4)
(5)
答案解析
1.C
2.B解:∵两张正方形纸片的面积分别为16cm2和12cm2,
∴它们的边长分别为=4cm,
=2cm,
∴AB=4cm,BC=(2+4)cm,
∴空白部分的面积=(2+4)×4﹣12﹣16,
=8+16﹣12﹣16,
=(﹣12+8)cm2.
3.A
4.B【解答】解:∵a>0,∴=a.
==﹣1.
5.C解:A.==,此选项错误;
B.÷==,此选项错误;
C.()2=3,此选项正确;
D.=2,此选项错误;
6.B
7.D
8.D
9.C【分析】根据给出的运算程序计算即可.
【解答】解:当n=时,n(n+1)=2+<15,
当n=2+时,n(n+1)=8+5>15,
【点评】本题考查的是二次根式的混合运算,掌握二次根式的混合运算法则是解题的关键.
10.D
11.0或-1
12.x≥-1
{解析}本题考查了分式有意义的条件,根据题意有:x+1≥0,∴x≥-1.
13.解:由题意,3-x>0,x-2≧0,所以2≦x<3.
14.0【解析】由图可知:a<0,b>0,
b-a>0,
∴
故填:0
15.4点拨:∵最简二次根式与可以合并,∴它们的被开方数相同,即3a-1=2a+3,解得a=4.
16.最简二次根式
被开方数
17.解:,
.
18.
19.(1)
(2)
(3)
(4)
20.(1);(2)2+
21.解:可以.
理由:第一个问题的解答是根据二次根式的定义,得出被开方数大于或等于0,从而求出x的取值范围;而第二个问题的解答也是根据二次根式的定义,得出被开方数大于或等于0,进而得出x的取值范围,这两题考查的知识及解答方法完全一样,所以可以如此转化.
22.(1)1;(2)xy
23.17.3
m.
24.(1);(2)16﹣12;(3);(4)20+6;(5)5+
