沪科版七年级下册数学9.3 分式方程课件 (共21张PPT)
文档属性
| 名称 | 沪科版七年级下册数学9.3 分式方程课件 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-07 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
分式方程
解:设该车提速前的速度为xkm/h,那么提速后的的速度为(1+25%)xkm/h。
由题意得:
5
创设情景
1.
什么叫做一元一次方程?
2.
下列方程哪些是一元一次方程?
3.
请解上述方程(4).
6
一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?
解:设江水的流速为
v
千米/时,根据题意,得
分母中含未知数的方程叫做分式方程.
情
境
问
题
7
分式方程
定义分母里含有未知数的方程叫做分式方程。
分母里不含有未知数的方程叫做整式方程。即目前方程包括整式方程与分式方程
思考—类比化归
(1)分式方程的特征是什么?
分式方程的特征是分母中含有未知数.
(2)如何解分式方程?
回顾:1.什么是方程的解?
2.在解有分母的一元一次方程中怎么去分母?
例如:
我们能不能效仿有分母的一元一次方程的解
法,想办法去掉分式方程的分母,把它转化
成整式方程?
9
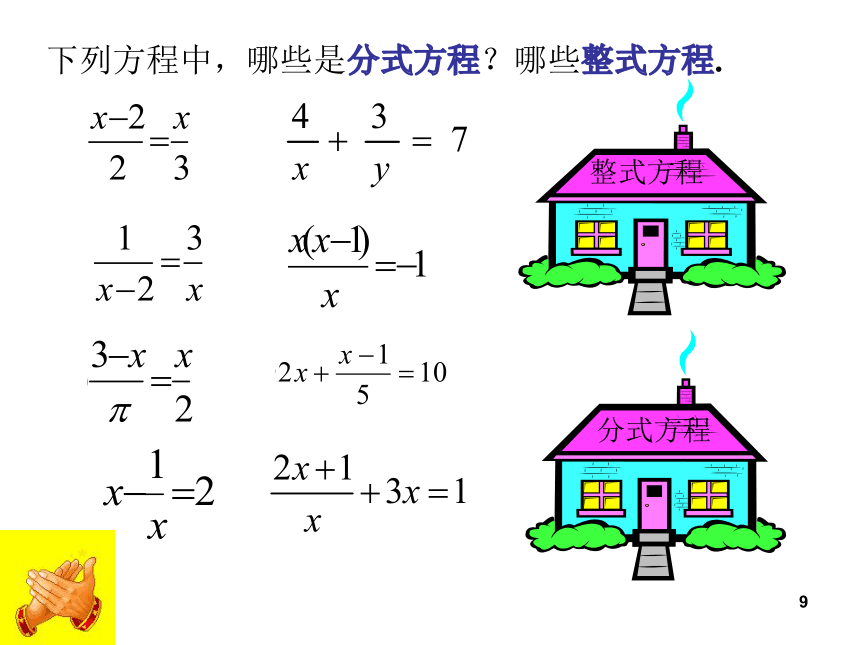
下列方程中,哪些是分式方程?哪些整式方程.
整式方程
分式方程
10
解得:x=80
下面我们一起研究下怎么样来解分式方程:
方程两边同乘以最简公分母(1+25%)x
,得:
2000-1600=5x
在解分式方程的过程中体现了一个非常重要的数学思想方法:转化的数学思想(化归思想)。
探究
检验:将x=80代入上述分式方程,左边=4=右边,所以x=80是原分式方程的解。(仅仅是为了看结果正、误?)
11
解得:
下面我们一起研究下怎么样来解分式方程:
方程两边同乘以(20+v)?(20-v)
,得:
在解分式方程的过程中体现了一个非常重要的数学思想方法:转化的数学思想(化归思想)。
探究
检验:将v=5代入分式方程,左边=4=右边,所以v=5是原分式方程的解。(仅仅是为了看结果正、误?)
100(20-v)=60(20+v)
归纳(一)
解分式方程的基本思路:
将分式方程化为整式方程。
具体做法是“去分母”,即方程两边同乘最简公分母。
这也是解分式方程的一般思路和做法。
13
解分式方程:
方程两边同乘以最简公分母(x-5)?(x+5),得:
x+5=10
解得:
x=5
检验:将x=5代入原分式方程,发现这时x-5和x2-25的值都为0,相应分式无意义。所以x=5不是原分式方程的解。由此可知检验不能省,必须做!
原分式方程无解。——结论必须下
为什么会产生增根?怎么办?
例1
解分式方程
2x=3x-9
解得x=9
检验:x=9时x(x-3)
≠0,x=9是原方程的解.
分式方程
整式方程
解整式方程
检
验
转化
①
②
③
解分式方程
解:
方程的两边同乘
x(x-3),得
例2
解分式方程
解:方程两边同乘以
(x-1)?(x+2), 得
化简,得x+2=3.
x(x+2)-1·(x-1)(x+2)=3
解得
x=1.
检验:x=1时(x-1)(x+2)
=0,x=1不是原方程的解.原方程无解.
一化二解三检验
16
归纳(二)解分式方程的一般步骤
1、
在方程的两边都乘以最简公分母,约去分母,化成整式方程.(约分后分子加括号,每项都需相乘)
2、解这个整式方程.
3、
把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则(等于0),这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.
解分式方程的思路是:
分式方程
整式方程
去分母
一化二解三验
四结论
17
解方程:
随堂练习
18
小结
分式方程概念及解法
分式方程
整式方程
去分母
解分式方程的一般步骤:
一化二解三检验
分式方程解法攻略
解方程须仔细,一步一步走下去:
公分母是个筐,分母因式它都装;
所有项莫要漏,分母去后加括号。
求解后要检验,认真判断最重要:
值为零请舍掉,不为零时才是真。
诸要点要牢记,分式方程也容易!
作业:(一)P109-3;
(二)同步9.3(一)。
再
见!
下课了!
分式方程
解:设该车提速前的速度为xkm/h,那么提速后的的速度为(1+25%)xkm/h。
由题意得:
5
创设情景
1.
什么叫做一元一次方程?
2.
下列方程哪些是一元一次方程?
3.
请解上述方程(4).
6
一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?
解:设江水的流速为
v
千米/时,根据题意,得
分母中含未知数的方程叫做分式方程.
情
境
问
题
7
分式方程
定义分母里含有未知数的方程叫做分式方程。
分母里不含有未知数的方程叫做整式方程。即目前方程包括整式方程与分式方程
思考—类比化归
(1)分式方程的特征是什么?
分式方程的特征是分母中含有未知数.
(2)如何解分式方程?
回顾:1.什么是方程的解?
2.在解有分母的一元一次方程中怎么去分母?
例如:
我们能不能效仿有分母的一元一次方程的解
法,想办法去掉分式方程的分母,把它转化
成整式方程?
9
下列方程中,哪些是分式方程?哪些整式方程.
整式方程
分式方程
10
解得:x=80
下面我们一起研究下怎么样来解分式方程:
方程两边同乘以最简公分母(1+25%)x
,得:
2000-1600=5x
在解分式方程的过程中体现了一个非常重要的数学思想方法:转化的数学思想(化归思想)。
探究
检验:将x=80代入上述分式方程,左边=4=右边,所以x=80是原分式方程的解。(仅仅是为了看结果正、误?)
11
解得:
下面我们一起研究下怎么样来解分式方程:
方程两边同乘以(20+v)?(20-v)
,得:
在解分式方程的过程中体现了一个非常重要的数学思想方法:转化的数学思想(化归思想)。
探究
检验:将v=5代入分式方程,左边=4=右边,所以v=5是原分式方程的解。(仅仅是为了看结果正、误?)
100(20-v)=60(20+v)
归纳(一)
解分式方程的基本思路:
将分式方程化为整式方程。
具体做法是“去分母”,即方程两边同乘最简公分母。
这也是解分式方程的一般思路和做法。
13
解分式方程:
方程两边同乘以最简公分母(x-5)?(x+5),得:
x+5=10
解得:
x=5
检验:将x=5代入原分式方程,发现这时x-5和x2-25的值都为0,相应分式无意义。所以x=5不是原分式方程的解。由此可知检验不能省,必须做!
原分式方程无解。——结论必须下
为什么会产生增根?怎么办?
例1
解分式方程
2x=3x-9
解得x=9
检验:x=9时x(x-3)
≠0,x=9是原方程的解.
分式方程
整式方程
解整式方程
检
验
转化
①
②
③
解分式方程
解:
方程的两边同乘
x(x-3),得
例2
解分式方程
解:方程两边同乘以
(x-1)?(x+2), 得
化简,得x+2=3.
x(x+2)-1·(x-1)(x+2)=3
解得
x=1.
检验:x=1时(x-1)(x+2)
=0,x=1不是原方程的解.原方程无解.
一化二解三检验
16
归纳(二)解分式方程的一般步骤
1、
在方程的两边都乘以最简公分母,约去分母,化成整式方程.(约分后分子加括号,每项都需相乘)
2、解这个整式方程.
3、
把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则(等于0),这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.
解分式方程的思路是:
分式方程
整式方程
去分母
一化二解三验
四结论
17
解方程:
随堂练习
18
小结
分式方程概念及解法
分式方程
整式方程
去分母
解分式方程的一般步骤:
一化二解三检验
分式方程解法攻略
解方程须仔细,一步一步走下去:
公分母是个筐,分母因式它都装;
所有项莫要漏,分母去后加括号。
求解后要检验,认真判断最重要:
值为零请舍掉,不为零时才是真。
诸要点要牢记,分式方程也容易!
作业:(一)P109-3;
(二)同步9.3(一)。
再
见!
下课了!
