沪科版九年级下册数学24.3圆周角定理及其推论课件 (共17张PPT)
文档属性
| 名称 | 沪科版九年级下册数学24.3圆周角定理及其推论课件 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 800.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
24.3
圆周角
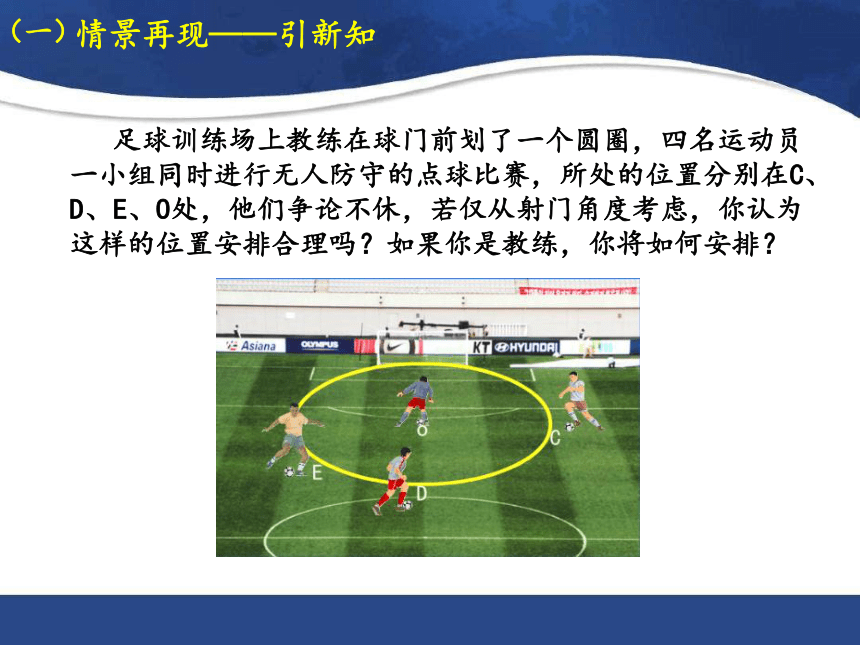
足球训练场上教练在球门前划了一个圆圈,四名运动员一小组同时进行无人防守的点球比赛,所处的位置分别在C、D、E、O处,他们争论不休,若仅从射门角度考虑,你认为这样的位置安排合理吗?如果你是教练,你将如何安排?
(一)
情景再现——引新知
(二)
有效探究——悟新知
探定义
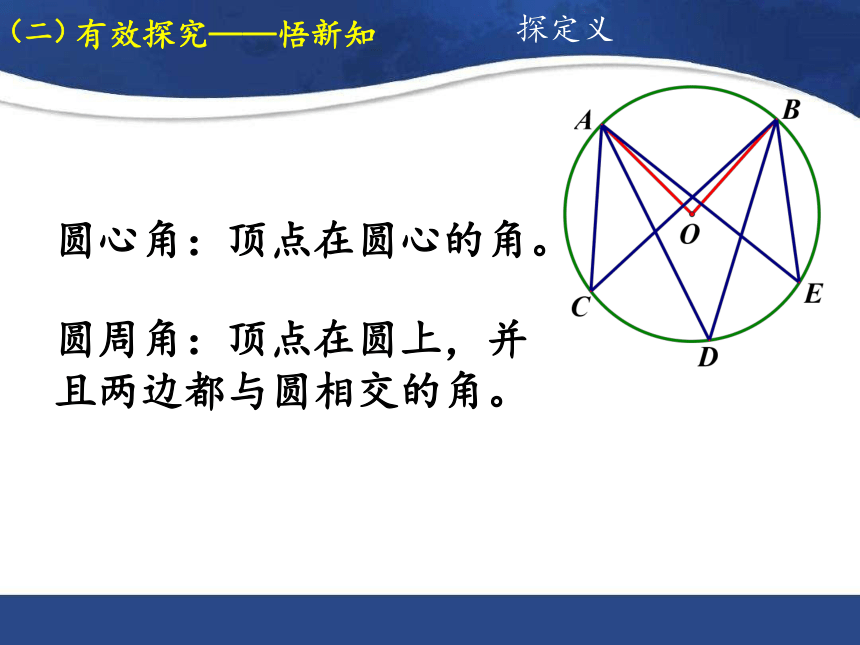
圆心角:顶点在圆心的角。
圆周角:顶点在圆上,并且两边都与圆相交的角。
探定义
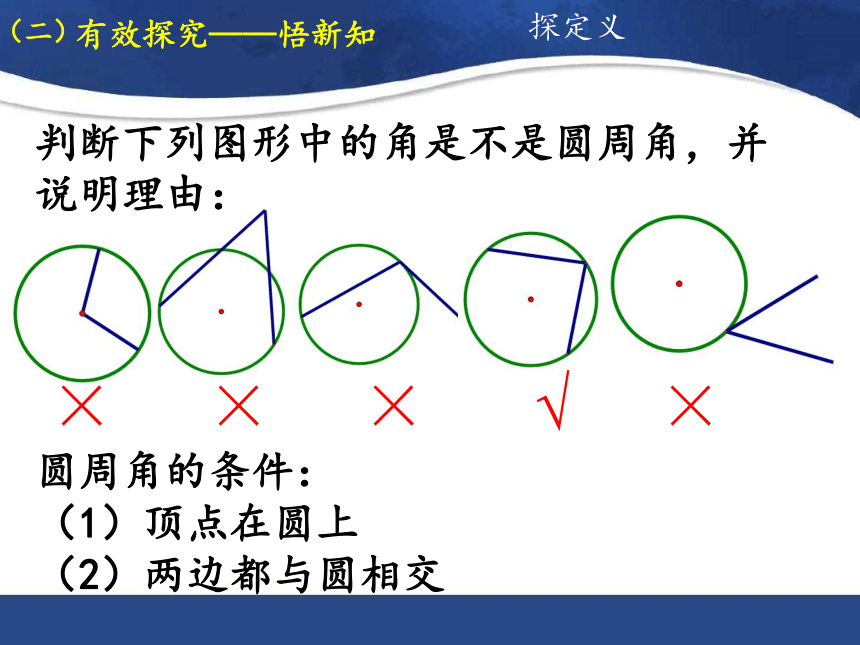
判断下列图形中的角是不是圆周角,并说明理由:
圆周角的条件:
(1)顶点在圆上
(2)两边都与圆相交
×
×
×
√
×
(二)
有效探究——悟新知
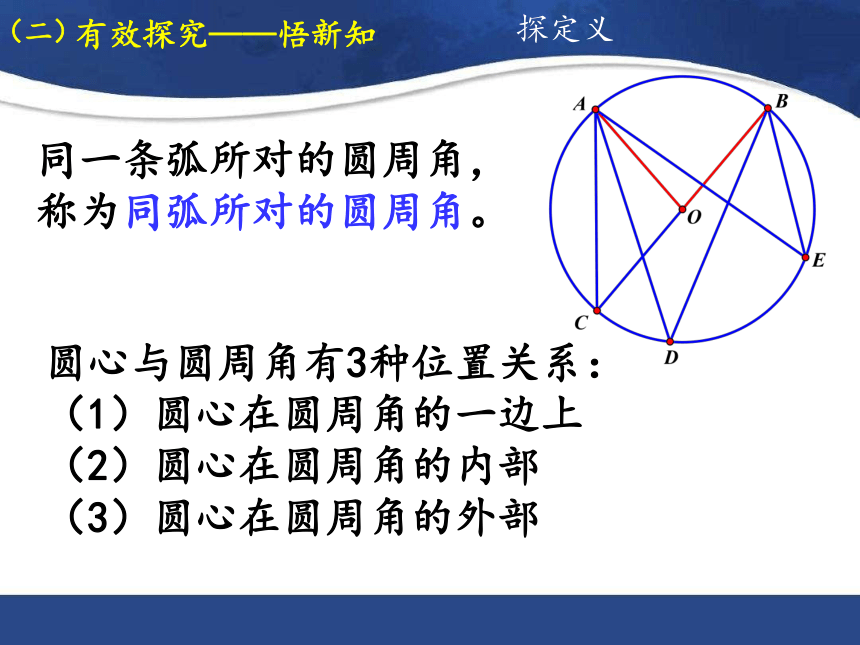
同一条弧所对的圆周角,称为同弧所对的圆周角。
圆心与圆周角有3种位置关系:
(1)圆心在圆周角的一边上
(2)圆心在圆周角的内部
(3)圆心在圆周角的外部
探定义
(二)
有效探究——悟新知
(2)请大家根据圆心与圆周角的位置关系,把小组内画出的图形进行分类,你能分为几类?
1、小组合作探究
(1)每个人在⊙O上任取一条弧AB,画出弧AB所对的一个圆周角和圆心角,测量它们的度数,你得到什么结论?
探定理——分类
(二)
有效探究——悟新知
探定理——分类
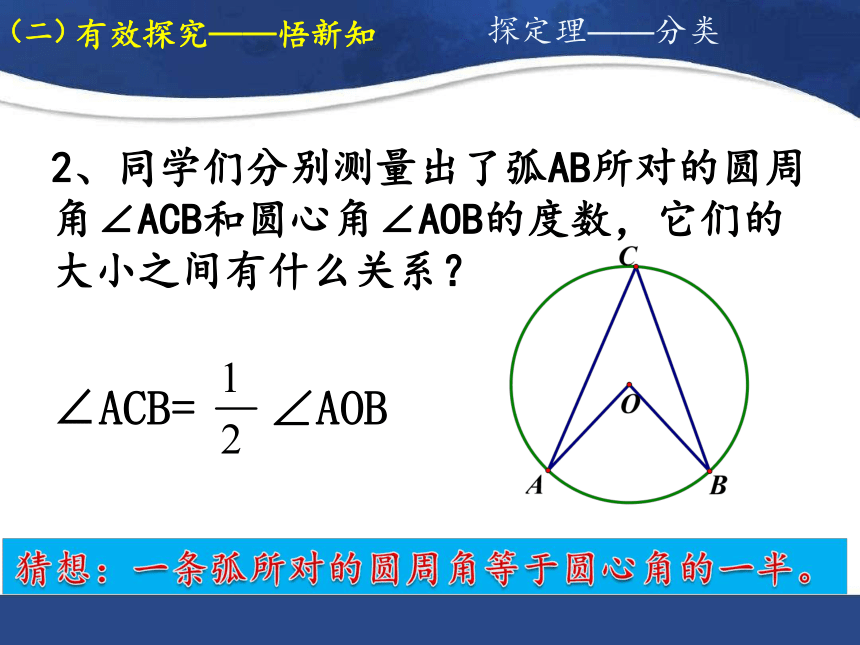
2、同学们分别测量出了弧AB所对的圆周角∠ACB和圆心角∠AOB的度数,它们的大小之间有什么关系?
∠ACB=
∠AOB
(二)
有效探究——悟新知
探定理——证明
第一种情况:
第二种情况:
∠1=
∠2,∠3=
∠4
∴
∠1
+∠3=
(∠2+∠4)
即:∠ACB
=
∠AOB
作直径CD,利用(1)
的结果,有
证得:∠2=
∠3
(二)
有效探究——悟新知
第二种情况:
第三种情况:
作直径CD,利用(1)
的结果,有
∠1=
∠2,∠3=
∠4
∴
∠1
+∠3=
(∠2+∠4)
即:∠ACB
=
∠AOB
作直径CD,利用(1)
的结果,有
∠1=
∠2,∠3=
∠4
∴
∠1
-∠3=
(∠2-∠4)
即:∠ACB
=
∠AOB
探定理——证明
(二)
有效探究——悟新知
圆周角定理:
一条弧所对的圆周角等于它所对圆心角的一半。
探推论
同弧所对的圆周角之间有什么关系?
例如图中∠C,∠D,∠E的大小有什么关系?
同弧所对的圆周角相等。
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等。
那等弧所对的圆周角相等吗?
为什么?
(二)
有效探究——悟新知
(二)
有效探究——悟新知
探定理——结论
结论:1、同弧所对的圆周角是圆心角的一半
2、同弧所对的圆周角相等
1、如图1,在⊙O中,∠BOC=50°,则∠BAC=
°
25
(三)
基础巩固——用新知
2、如图,在⊙O中,弦AB//CD,若∠ABC=40°,则∠BOD
=
80°
(三)
基础巩固——用新知
3、如图,在⊙O中,弦AB=3,圆周角∠C=30°,则⊙O的半径=
3
(三)
基础巩固——用新知
4、中考连接:
如图所示,点A、B、C、D在⊙O上,OA
BC,∠AOB=50°,求∠ADC的度数
解:连接BD,
则∠ADB=
∠AOB=25°
∵OA
BC
∴弧AC=弧AB
∴∠ADC=∠ADB=25°
(三)
基础巩固——用新知
(三)
反思回顾——拓新知
布置作业:
1、必做题
学练优第12页.
2、拓展题:如图,在足球比赛中,甲带球向对方球门AB进攻,当它带球冲到M点时,同伴乙已经助攻冲到C点,此时甲是直接射门好,还是将球传给乙,让乙射门好?
24.3
圆周角
足球训练场上教练在球门前划了一个圆圈,四名运动员一小组同时进行无人防守的点球比赛,所处的位置分别在C、D、E、O处,他们争论不休,若仅从射门角度考虑,你认为这样的位置安排合理吗?如果你是教练,你将如何安排?
(一)
情景再现——引新知
(二)
有效探究——悟新知
探定义
圆心角:顶点在圆心的角。
圆周角:顶点在圆上,并且两边都与圆相交的角。
探定义
判断下列图形中的角是不是圆周角,并说明理由:
圆周角的条件:
(1)顶点在圆上
(2)两边都与圆相交
×
×
×
√
×
(二)
有效探究——悟新知
同一条弧所对的圆周角,称为同弧所对的圆周角。
圆心与圆周角有3种位置关系:
(1)圆心在圆周角的一边上
(2)圆心在圆周角的内部
(3)圆心在圆周角的外部
探定义
(二)
有效探究——悟新知
(2)请大家根据圆心与圆周角的位置关系,把小组内画出的图形进行分类,你能分为几类?
1、小组合作探究
(1)每个人在⊙O上任取一条弧AB,画出弧AB所对的一个圆周角和圆心角,测量它们的度数,你得到什么结论?
探定理——分类
(二)
有效探究——悟新知
探定理——分类
2、同学们分别测量出了弧AB所对的圆周角∠ACB和圆心角∠AOB的度数,它们的大小之间有什么关系?
∠ACB=
∠AOB
(二)
有效探究——悟新知
探定理——证明
第一种情况:
第二种情况:
∠1=
∠2,∠3=
∠4
∴
∠1
+∠3=
(∠2+∠4)
即:∠ACB
=
∠AOB
作直径CD,利用(1)
的结果,有
证得:∠2=
∠3
(二)
有效探究——悟新知
第二种情况:
第三种情况:
作直径CD,利用(1)
的结果,有
∠1=
∠2,∠3=
∠4
∴
∠1
+∠3=
(∠2+∠4)
即:∠ACB
=
∠AOB
作直径CD,利用(1)
的结果,有
∠1=
∠2,∠3=
∠4
∴
∠1
-∠3=
(∠2-∠4)
即:∠ACB
=
∠AOB
探定理——证明
(二)
有效探究——悟新知
圆周角定理:
一条弧所对的圆周角等于它所对圆心角的一半。
探推论
同弧所对的圆周角之间有什么关系?
例如图中∠C,∠D,∠E的大小有什么关系?
同弧所对的圆周角相等。
推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等。
那等弧所对的圆周角相等吗?
为什么?
(二)
有效探究——悟新知
(二)
有效探究——悟新知
探定理——结论
结论:1、同弧所对的圆周角是圆心角的一半
2、同弧所对的圆周角相等
1、如图1,在⊙O中,∠BOC=50°,则∠BAC=
°
25
(三)
基础巩固——用新知
2、如图,在⊙O中,弦AB//CD,若∠ABC=40°,则∠BOD
=
80°
(三)
基础巩固——用新知
3、如图,在⊙O中,弦AB=3,圆周角∠C=30°,则⊙O的半径=
3
(三)
基础巩固——用新知
4、中考连接:
如图所示,点A、B、C、D在⊙O上,OA
BC,∠AOB=50°,求∠ADC的度数
解:连接BD,
则∠ADB=
∠AOB=25°
∵OA
BC
∴弧AC=弧AB
∴∠ADC=∠ADB=25°
(三)
基础巩固——用新知
(三)
反思回顾——拓新知
布置作业:
1、必做题
学练优第12页.
2、拓展题:如图,在足球比赛中,甲带球向对方球门AB进攻,当它带球冲到M点时,同伴乙已经助攻冲到C点,此时甲是直接射门好,还是将球传给乙,让乙射门好?
