人教版八年级数学下册第二十章 数据的分析章末复习卷(含答案)
文档属性
| 名称 | 人教版八年级数学下册第二十章 数据的分析章末复习卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 336.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-06 00:00:00 | ||
图片预览




文档简介
人教版八年级数学下册第二十章
数据的分析
章末复习卷
选择题
1.一组数据3,4,5,6,7的方差是(
)
A.2
B.3
C.4
D.5
2.已知一组数据的平均数为,若在这组数据中再添加一个数,则所得新数据的方差与原数据的方差相比较(
)
A.变大
B.变小
C.相等
D.无法确定
3.了解八年级某班学生每天睡眠时间情况如下(睡眠时间为x个小时):5≤x<6有1人,6≤x<7有3人,7≤x<8有4人,8≤x<9有40人,9≤x<10有2人.估计八年级学生平均睡眠时间为(
)
A.6~7小时
B.7~8小时
C.8~9小时
D.9~10小时
4.为了迎接今年的国庆节,八(3)、八(5)班举行跳绳比赛,各班参赛选手每分钟跳绳的次数经统计计算后填入下表:
班级
参加人数
(人)
中位数
(次/分)
方差
平均次数
(次/分)
八(3)班
45
171
9.54
155
八(5)班
45
169
16.32
155
某同学根据表格得出如下结论:①八(3)、八(5)班跳绳的平均水平相同.②若跳绳速度多于每分钟170次的算作优秀,则八(3)班优秀人数不少于八(5)班.③八(5)班跳绳比赛成绩波动情况比八(3)班成绩的波动大.上述结论正确的个数有
(
)
A.3个
B.2个
C.1个
D.0个
5.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是(
)
A.255分
B.84分
C.84.5分
D.86分
6.已知一组数据x1,x2,x3如下表,那么另一组数据2x1-1,2x2-1,2x3-1的平均数和方差分别是(
)
x1
x2
x3
1
2
3
A.2, B.3,
C.3, D.3,
7.为响应“节约用水”的号召,小刚随机调查了班级35名同学中5名同学家庭一年的平均用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是(
)
A.8,8
B.8.4,8
C.8.4,8.4
D.8,8.4
8.9.8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为(
)
A.76
B.75
C.74
D.73
9.自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是(
)
A.3
B.4
C.5
D.6
10.甲、乙、丙、丁四人的数学测验成绩分别为90分、90分、x分、80分,若这组数据的平均数恰好等于90分,则这组数据的中位数是(
)
A.100分
B.95分
C.90分
D.85分
填空题
11.某学生在一次考试中,语文、数学、英语三门学科的平均成绩是80分,物理、化学两门学科的平均成绩为85分,则该学生这五门学科的平均成绩
.?
12.已知三个不相等的正整数的平均数、中位数都是3,则这三个数分别为
.?
13.有一组数据如下:3,a,4,6,7.如果它们的平均数是5,那么这组数据的方差为 .?
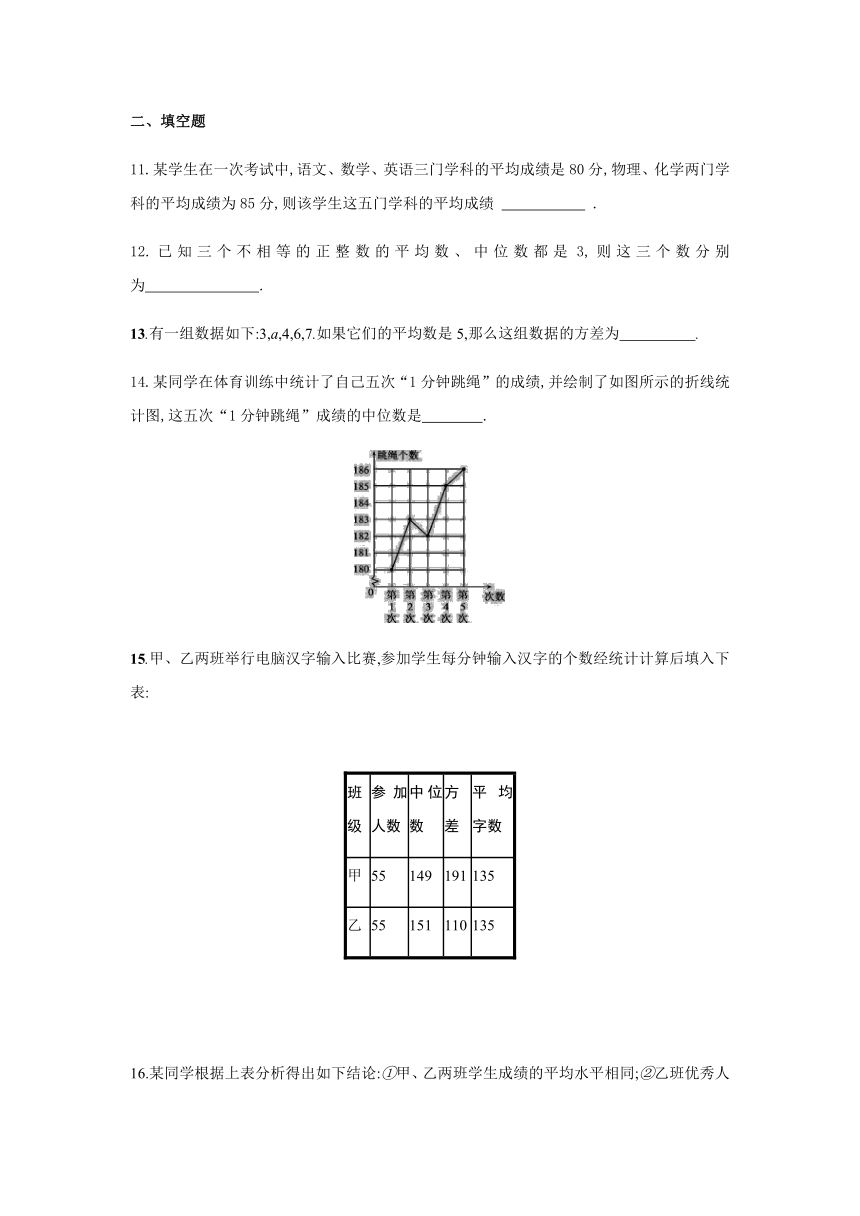
14.某同学在体育训练中统计了自己五次“1分钟跳绳”的成绩,并绘制了如图所示的折线统计图,这五次“1分钟跳绳”成绩的中位数是 .?
15.甲、乙两班举行电脑汉字输入比赛,参加学生每分钟输入汉字的个数经统计计算后填入下表:
班级
参加人数
中位数
方差
平均字数
甲
55
149
191
135
乙
55
151
110
135
16.某同学根据上表分析得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀人数多于甲班优秀人数(每分钟输入汉字数≥150个为优秀);③甲班的成绩波动比乙班的成绩波动大.上述结论正确的是 .(填序号)?
三、解答题
17.某校为了解全校2
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
18.方差的算术平方根叫做标准差,即s=,标准差的单位与原始数据的单位相同,实际中我们常用它来度量数据的波动程度.请你利用标准差解决下面的问题:
一次期末考试中,A,B,C,D,E五名同学的数学、英语成绩等有关信息如下表所示(单位:分):
A
B
C
D
E
平均分
标准差
数学
71
72
69
68
70
英语
88
82
94
85
76
85
(1)求这五名同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择.标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与英语哪个学科考得更好?
19.公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄(单位:岁)如下:
甲群游客:13,13,14,15,15,15,15,16,17,17;
乙群游客:3,4,4,5,5,6,6,6,54,57.
(1)甲群游客的平均年龄是多少?中位数、众数呢?其中能较好反映甲群游客年龄特征的是什么?
(2)乙群游客的平均年龄是多少?中位数、众数呢?其中能较好反映乙群游客年龄特征的是什么?
20.为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了统计表和统计图.
甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
0
乙
1
甲、乙射击成绩折线图
(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,那么你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,那么应该制定怎样的评判规则?为什么?
参考答案
一、选择题
1.一组数据3,4,5,6,7的方差是( A )
A.2
B.3
C.4
D.5
2.已知一组数据的平均数为,若在这组数据中再添加一个数,则所得新数据的方差与原数据的方差相比较( B )
A.变大
B.变小
C.相等
D.无法确定
3.了解八年级某班学生每天睡眠时间情况如下(睡眠时间为x个小时):5≤x<6有1人,6≤x<7有3人,7≤x<8有4人,8≤x<9有40人,9≤x<10有2人.估计八年级学生平均睡眠时间为(
C
)
A.6~7小时
B.7~8小时
C.8~9小时
D.9~10小时
4.为了迎接今年的国庆节,八(3)、八(5)班举行跳绳比赛,各班参赛选手每分钟跳绳的次数经统计计算后填入下表:
班级
参加人数
(人)
中位数
(次/分)
方差
平均次数
(次/分)
八(3)班
45
171
9.54
155
八(5)班
45
169
16.32
155
某同学根据表格得出如下结论:①八(3)、八(5)班跳绳的平均水平相同.②若跳绳速度多于每分钟170次的算作优秀,则八(3)班优秀人数不少于八(5)班.③八(5)班跳绳比赛成绩波动情况比八(3)班成绩的波动大.上述结论正确的个数有
( A )
A.3个
B.2个
C.1个
D.0个
5.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是( D )
A.255分
B.84分
C.84.5分
D.86分
6.已知一组数据x1,x2,x3如下表,那么另一组数据2x1-1,2x2-1,2x3-1的平均数和方差分别是( D )
x1
x2
x3
1
2
3
A.2, B.3,
C.3, D.3,
7.为响应“节约用水”的号召,小刚随机调查了班级35名同学中5名同学家庭一年的平均用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是( B )
A.8,8
B.8.4,8
C.8.4,8.4
D.8,8.4
8.9.8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为( A
)
A.76
B.75
C.74
D.73
9.自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是( C )
A.3
B.4
C.5
D.6
10.甲、乙、丙、丁四人的数学测验成绩分别为90分、90分、x分、80分,若这组数据的平均数恰好等于90分,则这组数据的中位数是(
A
)
A.100分
B.95分
C.90分
D.85分
填空题
11.某学生在一次考试中,语文、数学、英语三门学科的平均成绩是80分,物理、化学两门学科的平均成绩为85分,则该学生这五门学科的平均成绩
82
.?
12.已知三个不相等的正整数的平均数、中位数都是3,则这三个数分别为 1,3,5或2,3,4 .?
13.有一组数据如下:3,a,4,6,7.如果它们的平均数是5,那么这组数据的方差为 2 .?
14.某同学在体育训练中统计了自己五次“1分钟跳绳”的成绩,并绘制了如图所示的折线统计图,这五次“1分钟跳绳”成绩的中位数是 183 .?
15.甲、乙两班举行电脑汉字输入比赛,参加学生每分钟输入汉字的个数经统计计算后填入下表:
班级
参加人数
中位数
方差
平均字数
甲
55
149
191
135
乙
55
151
110
135
16.某同学根据上表分析得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀人数多于甲班优秀人数(每分钟输入汉字数≥150个为优秀);③甲班的成绩波动比乙班的成绩波动大.上述结论正确的是 ①②③ .(填序号)?
三、解答题
17.某校为了解全校2
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
解:(1)=(0.5×15+1.0×20+1.5×10+2.0×5)=1.05(小时),
这50名学生在这一天平均每人的课外阅读所用时间是1.05小时.
(2)2
000×=1
400(人),
所以全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有1
400人.
18.方差的算术平方根叫做标准差,即s=,标准差的单位与原始数据的单位相同,实际中我们常用它来度量数据的波动程度.请你利用标准差解决下面的问题:
一次期末考试中,A,B,C,D,E五名同学的数学、英语成绩等有关信息如下表所示(单位:分):
A
B
C
D
E
平均分
标准差
数学
71
72
69
68
70
英语
88
82
94
85
76
85
(1)求这五名同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择.标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与英语哪个学科考得更好?
解
(1)平均分为(71+72+69+68+70)=70;
标准差为
=6.
(2)数学标准分为(71-70)÷≈0.7;
英语标准分为(88-85)÷6=0.5.
因此,从标准分来看,A同学的数学比英语考得更好.
19.公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄(单位:岁)如下:
甲群游客:13,13,14,15,15,15,15,16,17,17;
乙群游客:3,4,4,5,5,6,6,6,54,57.
(1)甲群游客的平均年龄是多少?中位数、众数呢?其中能较好反映甲群游客年龄特征的是什么?
(2)乙群游客的平均年龄是多少?中位数、众数呢?其中能较好反映乙群游客年龄特征的是什么?
解析 (1)甲群游客的平均年龄是(13+13+14+15+15+15+15+16+17+17)÷10=15(岁),
中位数是(15+15)÷2=15岁,众数是15岁,
其中能较好反映甲群游客年龄特征的是平均数,中位数,众数.
(2)乙群游客的平均年龄是(3+4+4+5+5+6+6+6+54+57)÷10=15(岁),
中位数是(5+6)÷2=5.5岁,众数是6岁,
其中能较好反映乙群游客年龄特征的是中位数和众数.
20.为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了统计表和统计图.
甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
0
乙
1
甲、乙射击成绩折线图
(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,那么你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,那么应该制定怎样的评判规则?为什么?
解
(1)根据折线统计图得乙的射击成绩为2,4,6,7,7,8,8,9,9,10,则平均数为=7,中位数为7.5,方差为×[(2-7)2+(4-7)2+(6-7)2+(8-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2+(10-7)2]=5.4.
由表知甲的射击成绩的平均数为7,则甲第8次的射击成绩为70-(9+6+7+6+5+7+7+8+9)=6(环),故10次射击成绩为5,6,6,6,7,7,7,8,9,9,中位数为7,方差为×[(5-7)2+(6-7)2+(6-7)2+(6-7)2+(7-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2]=1.6,补全图表如下:
甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
7
1.6
0
乙
7
7.5
5.4
1
甲、乙射击成绩折线图
(2)因为两人射击成绩的平均数相同,但甲成绩的方差小于乙成绩的方差,所以甲胜出.
(3)希望乙胜出,规则为命中9环与10环的总数大的胜出.因为乙命中9环与10环的总数为3次,而甲只命中2次.
数据的分析
章末复习卷
选择题
1.一组数据3,4,5,6,7的方差是(
)
A.2
B.3
C.4
D.5
2.已知一组数据的平均数为,若在这组数据中再添加一个数,则所得新数据的方差与原数据的方差相比较(
)
A.变大
B.变小
C.相等
D.无法确定
3.了解八年级某班学生每天睡眠时间情况如下(睡眠时间为x个小时):5≤x<6有1人,6≤x<7有3人,7≤x<8有4人,8≤x<9有40人,9≤x<10有2人.估计八年级学生平均睡眠时间为(
)
A.6~7小时
B.7~8小时
C.8~9小时
D.9~10小时
4.为了迎接今年的国庆节,八(3)、八(5)班举行跳绳比赛,各班参赛选手每分钟跳绳的次数经统计计算后填入下表:
班级
参加人数
(人)
中位数
(次/分)
方差
平均次数
(次/分)
八(3)班
45
171
9.54
155
八(5)班
45
169
16.32
155
某同学根据表格得出如下结论:①八(3)、八(5)班跳绳的平均水平相同.②若跳绳速度多于每分钟170次的算作优秀,则八(3)班优秀人数不少于八(5)班.③八(5)班跳绳比赛成绩波动情况比八(3)班成绩的波动大.上述结论正确的个数有
(
)
A.3个
B.2个
C.1个
D.0个
5.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是(
)
A.255分
B.84分
C.84.5分
D.86分
6.已知一组数据x1,x2,x3如下表,那么另一组数据2x1-1,2x2-1,2x3-1的平均数和方差分别是(
)
x1
x2
x3
1
2
3
A.2, B.3,
C.3, D.3,
7.为响应“节约用水”的号召,小刚随机调查了班级35名同学中5名同学家庭一年的平均用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是(
)
A.8,8
B.8.4,8
C.8.4,8.4
D.8,8.4
8.9.8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为(
)
A.76
B.75
C.74
D.73
9.自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是(
)
A.3
B.4
C.5
D.6
10.甲、乙、丙、丁四人的数学测验成绩分别为90分、90分、x分、80分,若这组数据的平均数恰好等于90分,则这组数据的中位数是(
)
A.100分
B.95分
C.90分
D.85分
填空题
11.某学生在一次考试中,语文、数学、英语三门学科的平均成绩是80分,物理、化学两门学科的平均成绩为85分,则该学生这五门学科的平均成绩
.?
12.已知三个不相等的正整数的平均数、中位数都是3,则这三个数分别为
.?
13.有一组数据如下:3,a,4,6,7.如果它们的平均数是5,那么这组数据的方差为 .?
14.某同学在体育训练中统计了自己五次“1分钟跳绳”的成绩,并绘制了如图所示的折线统计图,这五次“1分钟跳绳”成绩的中位数是 .?
15.甲、乙两班举行电脑汉字输入比赛,参加学生每分钟输入汉字的个数经统计计算后填入下表:
班级
参加人数
中位数
方差
平均字数
甲
55
149
191
135
乙
55
151
110
135
16.某同学根据上表分析得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀人数多于甲班优秀人数(每分钟输入汉字数≥150个为优秀);③甲班的成绩波动比乙班的成绩波动大.上述结论正确的是 .(填序号)?
三、解答题
17.某校为了解全校2
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
18.方差的算术平方根叫做标准差,即s=,标准差的单位与原始数据的单位相同,实际中我们常用它来度量数据的波动程度.请你利用标准差解决下面的问题:
一次期末考试中,A,B,C,D,E五名同学的数学、英语成绩等有关信息如下表所示(单位:分):
A
B
C
D
E
平均分
标准差
数学
71
72
69
68
70
英语
88
82
94
85
76
85
(1)求这五名同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择.标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与英语哪个学科考得更好?
19.公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄(单位:岁)如下:
甲群游客:13,13,14,15,15,15,15,16,17,17;
乙群游客:3,4,4,5,5,6,6,6,54,57.
(1)甲群游客的平均年龄是多少?中位数、众数呢?其中能较好反映甲群游客年龄特征的是什么?
(2)乙群游客的平均年龄是多少?中位数、众数呢?其中能较好反映乙群游客年龄特征的是什么?
20.为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了统计表和统计图.
甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
0
乙
1
甲、乙射击成绩折线图
(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,那么你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,那么应该制定怎样的评判规则?为什么?
参考答案
一、选择题
1.一组数据3,4,5,6,7的方差是( A )
A.2
B.3
C.4
D.5
2.已知一组数据的平均数为,若在这组数据中再添加一个数,则所得新数据的方差与原数据的方差相比较( B )
A.变大
B.变小
C.相等
D.无法确定
3.了解八年级某班学生每天睡眠时间情况如下(睡眠时间为x个小时):5≤x<6有1人,6≤x<7有3人,7≤x<8有4人,8≤x<9有40人,9≤x<10有2人.估计八年级学生平均睡眠时间为(
C
)
A.6~7小时
B.7~8小时
C.8~9小时
D.9~10小时
4.为了迎接今年的国庆节,八(3)、八(5)班举行跳绳比赛,各班参赛选手每分钟跳绳的次数经统计计算后填入下表:
班级
参加人数
(人)
中位数
(次/分)
方差
平均次数
(次/分)
八(3)班
45
171
9.54
155
八(5)班
45
169
16.32
155
某同学根据表格得出如下结论:①八(3)、八(5)班跳绳的平均水平相同.②若跳绳速度多于每分钟170次的算作优秀,则八(3)班优秀人数不少于八(5)班.③八(5)班跳绳比赛成绩波动情况比八(3)班成绩的波动大.上述结论正确的个数有
( A )
A.3个
B.2个
C.1个
D.0个
5.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是( D )
A.255分
B.84分
C.84.5分
D.86分
6.已知一组数据x1,x2,x3如下表,那么另一组数据2x1-1,2x2-1,2x3-1的平均数和方差分别是( D )
x1
x2
x3
1
2
3
A.2, B.3,
C.3, D.3,
7.为响应“节约用水”的号召,小刚随机调查了班级35名同学中5名同学家庭一年的平均用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是( B )
A.8,8
B.8.4,8
C.8.4,8.4
D.8,8.4
8.9.8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为( A
)
A.76
B.75
C.74
D.73
9.自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是( C )
A.3
B.4
C.5
D.6
10.甲、乙、丙、丁四人的数学测验成绩分别为90分、90分、x分、80分,若这组数据的平均数恰好等于90分,则这组数据的中位数是(
A
)
A.100分
B.95分
C.90分
D.85分
填空题
11.某学生在一次考试中,语文、数学、英语三门学科的平均成绩是80分,物理、化学两门学科的平均成绩为85分,则该学生这五门学科的平均成绩
82
.?
12.已知三个不相等的正整数的平均数、中位数都是3,则这三个数分别为 1,3,5或2,3,4 .?
13.有一组数据如下:3,a,4,6,7.如果它们的平均数是5,那么这组数据的方差为 2 .?
14.某同学在体育训练中统计了自己五次“1分钟跳绳”的成绩,并绘制了如图所示的折线统计图,这五次“1分钟跳绳”成绩的中位数是 183 .?
15.甲、乙两班举行电脑汉字输入比赛,参加学生每分钟输入汉字的个数经统计计算后填入下表:
班级
参加人数
中位数
方差
平均字数
甲
55
149
191
135
乙
55
151
110
135
16.某同学根据上表分析得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀人数多于甲班优秀人数(每分钟输入汉字数≥150个为优秀);③甲班的成绩波动比乙班的成绩波动大.上述结论正确的是 ①②③ .(填序号)?
三、解答题
17.某校为了解全校2
000名学生的课外阅读情况,在全校范围内随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,将结果绘制成条形统计图(如图所示).
(1)这50名学生在这一天平均每人的课外阅读所用时间是多少?
(2)请你根据以上调查,估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人?
解:(1)=(0.5×15+1.0×20+1.5×10+2.0×5)=1.05(小时),
这50名学生在这一天平均每人的课外阅读所用时间是1.05小时.
(2)2
000×=1
400(人),
所以全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有1
400人.
18.方差的算术平方根叫做标准差,即s=,标准差的单位与原始数据的单位相同,实际中我们常用它来度量数据的波动程度.请你利用标准差解决下面的问题:
一次期末考试中,A,B,C,D,E五名同学的数学、英语成绩等有关信息如下表所示(单位:分):
A
B
C
D
E
平均分
标准差
数学
71
72
69
68
70
英语
88
82
94
85
76
85
(1)求这五名同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择.标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与英语哪个学科考得更好?
解
(1)平均分为(71+72+69+68+70)=70;
标准差为
=6.
(2)数学标准分为(71-70)÷≈0.7;
英语标准分为(88-85)÷6=0.5.
因此,从标准分来看,A同学的数学比英语考得更好.
19.公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄(单位:岁)如下:
甲群游客:13,13,14,15,15,15,15,16,17,17;
乙群游客:3,4,4,5,5,6,6,6,54,57.
(1)甲群游客的平均年龄是多少?中位数、众数呢?其中能较好反映甲群游客年龄特征的是什么?
(2)乙群游客的平均年龄是多少?中位数、众数呢?其中能较好反映乙群游客年龄特征的是什么?
解析 (1)甲群游客的平均年龄是(13+13+14+15+15+15+15+16+17+17)÷10=15(岁),
中位数是(15+15)÷2=15岁,众数是15岁,
其中能较好反映甲群游客年龄特征的是平均数,中位数,众数.
(2)乙群游客的平均年龄是(3+4+4+5+5+6+6+6+54+57)÷10=15(岁),
中位数是(5+6)÷2=5.5岁,众数是6岁,
其中能较好反映乙群游客年龄特征的是中位数和众数.
20.为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了统计表和统计图.
甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
0
乙
1
甲、乙射击成绩折线图
(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,那么你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,那么应该制定怎样的评判规则?为什么?
解
(1)根据折线统计图得乙的射击成绩为2,4,6,7,7,8,8,9,9,10,则平均数为=7,中位数为7.5,方差为×[(2-7)2+(4-7)2+(6-7)2+(8-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2+(10-7)2]=5.4.
由表知甲的射击成绩的平均数为7,则甲第8次的射击成绩为70-(9+6+7+6+5+7+7+8+9)=6(环),故10次射击成绩为5,6,6,6,7,7,7,8,9,9,中位数为7,方差为×[(5-7)2+(6-7)2+(6-7)2+(6-7)2+(7-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2]=1.6,补全图表如下:
甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
7
1.6
0
乙
7
7.5
5.4
1
甲、乙射击成绩折线图
(2)因为两人射击成绩的平均数相同,但甲成绩的方差小于乙成绩的方差,所以甲胜出.
(3)希望乙胜出,规则为命中9环与10环的总数大的胜出.因为乙命中9环与10环的总数为3次,而甲只命中2次.
