北师大版九年级下册数学 1.5 三角函数的应用课件(共21张PPT)
文档属性
| 名称 | 北师大版九年级下册数学 1.5 三角函数的应用课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 11:02:28 | ||
图片预览







文档简介
(共21张PPT)
课题你来猜?
九年级数学(下)第一章
直角三角形的边角关系
§1.5
三角函数的应用
??
船有触礁的危险吗?
驶向胜利的彼岸
2、直角三角形两锐角的关系:
直角三角形的边角关系
1、直角三角形三边的关系:
4、特殊角300,450,600角的三角函数值.
3、直角三角形边与角之间的关系:
勾股定理
a2+b2=c2.
两锐角互余
∠A+∠B=90°.
锐角三角函数
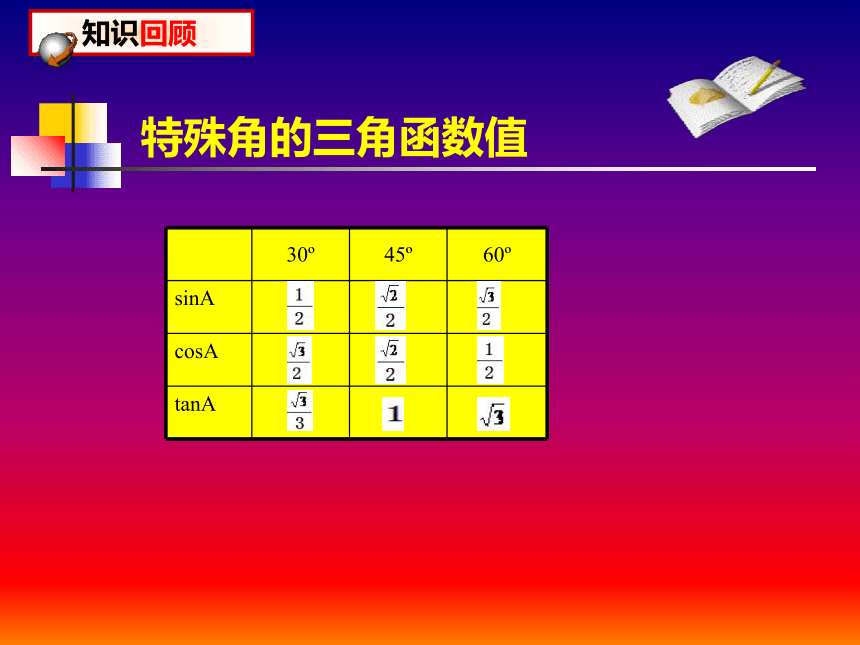
特殊角的三角函数值
30?
45?
60?
sinA
cosA
tanA
B
船有触礁的危险吗?
茫茫大海中有一个小岛A,该岛四周10海里内有暗礁.若也门撤侨行动中我国军舰由东向西航行,开始在A岛南偏东550的B处,往西行驶20海里后到达该岛的南偏东250的C处。之后,我国舰船继续向西航行。
观测点
被观测点
A
B
25?
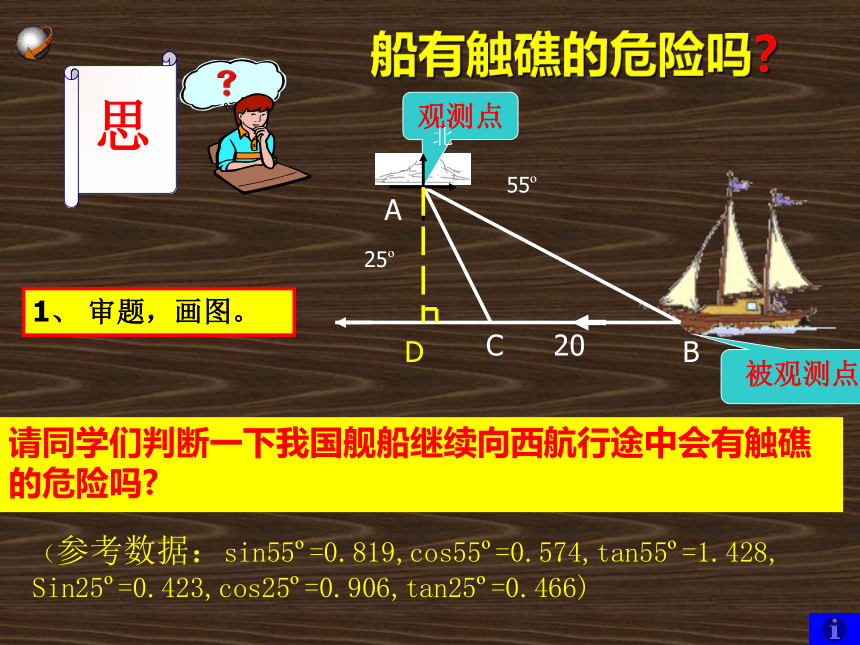
船有触礁的危险吗?
1、
审题,画图。
观测点
被观测点
A
请同学们判断一下我国舰船继续向西航行途中会有触礁的危险吗?
(参考数据:sin55?=0.819,cos55?=0.574,tan55?=1.428,
Sin25?=0.423,cos25?=0.906,tan25?=0.466)
B
C
20
D
A
x
2、审图,确定已知和未知。
3、解直角三角形,列方程(组)。
解:根据题意可知,∠BAD=550,
∠CAD=250,BC=
20海里.
设AD=x,则
答:货轮继续向东航行途中没有触礁的危险.
4、解方程(组),结论。
一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A处测得某灯塔位于它的北偏东30?的B处。上午9时行至C处,测得灯塔恰好在它的正北方向,此时它与灯塔的距离
是
海里。(结果保留根号)
真知在实践中诞生
(提示:由题意得,∠B=30?,BC⊥AC,AC=20海里。求CB)
20
A
B
C
N
东
CB⊥AC
300
古塔究竟有多高
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高?(小明的身高忽略不计,结果精确到1m).
要解决这问题,我们仍需将其数学化.
请与同伴交流你是怎么想的?
准备怎么去做?
现在你能完成这个任务吗?
行家看“门道”
这个图形与前面的图形相同,因此转化为数学问题为:
如图,根据题意可知,∠A=300,∠DBC=600,AB=50m.求CD的长。
答:该塔约有43m高.
解:如图,根据题意可知,∠A=300,∠DBC=600,AB=50m.设CD=x,则∠ADC=600,∠BDC=300,
楼梯加长了多少
项城某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯多占多长一段地面?(结果精确到0.01m).
(sin
400=0.643。tan400=0.839。tan350=0.700)
请与同伴交流你是怎么想的?
准备怎么去做?
联想的功能
这样做
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求
AD的长.
答:楼梯多占约0.61m一段地面.
钢缆长几何
如图,一灯柱AB被一钢缆CD固定.CD与地面成450夹角,且DB=6m.现再在CD上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少?
怎么做?
我先将它数学化!
结
解题思路导图
实际问题
图形分析
生活问题数学化
(构造直角三角形)
设未知量
解答问题
(构建三角函数模型)
(代入数据求解)
求解方程
数学问题
建立方程
谈
收获
1.知识收获
2.情感升华
课后作业
P21:1、2、3、4
1、数学源于生活
又应用于生活。
2、数学是思维的体操。
同学们,请尽情的舞动吧!
结束寄语
课题你来猜?
九年级数学(下)第一章
直角三角形的边角关系
§1.5
三角函数的应用
??
船有触礁的危险吗?
驶向胜利的彼岸
2、直角三角形两锐角的关系:
直角三角形的边角关系
1、直角三角形三边的关系:
4、特殊角300,450,600角的三角函数值.
3、直角三角形边与角之间的关系:
勾股定理
a2+b2=c2.
两锐角互余
∠A+∠B=90°.
锐角三角函数
特殊角的三角函数值
30?
45?
60?
sinA
cosA
tanA
B
船有触礁的危险吗?
茫茫大海中有一个小岛A,该岛四周10海里内有暗礁.若也门撤侨行动中我国军舰由东向西航行,开始在A岛南偏东550的B处,往西行驶20海里后到达该岛的南偏东250的C处。之后,我国舰船继续向西航行。
观测点
被观测点
A
B
25?
船有触礁的危险吗?
1、
审题,画图。
观测点
被观测点
A
请同学们判断一下我国舰船继续向西航行途中会有触礁的危险吗?
(参考数据:sin55?=0.819,cos55?=0.574,tan55?=1.428,
Sin25?=0.423,cos25?=0.906,tan25?=0.466)
B
C
20
D
A
x
2、审图,确定已知和未知。
3、解直角三角形,列方程(组)。
解:根据题意可知,∠BAD=550,
∠CAD=250,BC=
20海里.
设AD=x,则
答:货轮继续向东航行途中没有触礁的危险.
4、解方程(组),结论。
一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A处测得某灯塔位于它的北偏东30?的B处。上午9时行至C处,测得灯塔恰好在它的正北方向,此时它与灯塔的距离
是
海里。(结果保留根号)
真知在实践中诞生
(提示:由题意得,∠B=30?,BC⊥AC,AC=20海里。求CB)
20
A
B
C
N
东
CB⊥AC
300
古塔究竟有多高
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高?(小明的身高忽略不计,结果精确到1m).
要解决这问题,我们仍需将其数学化.
请与同伴交流你是怎么想的?
准备怎么去做?
现在你能完成这个任务吗?
行家看“门道”
这个图形与前面的图形相同,因此转化为数学问题为:
如图,根据题意可知,∠A=300,∠DBC=600,AB=50m.求CD的长。
答:该塔约有43m高.
解:如图,根据题意可知,∠A=300,∠DBC=600,AB=50m.设CD=x,则∠ADC=600,∠BDC=300,
楼梯加长了多少
项城某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯多占多长一段地面?(结果精确到0.01m).
(sin
400=0.643。tan400=0.839。tan350=0.700)
请与同伴交流你是怎么想的?
准备怎么去做?
联想的功能
这样做
解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求
AD的长.
答:楼梯多占约0.61m一段地面.
钢缆长几何
如图,一灯柱AB被一钢缆CD固定.CD与地面成450夹角,且DB=6m.现再在CD上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少?
怎么做?
我先将它数学化!
结
解题思路导图
实际问题
图形分析
生活问题数学化
(构造直角三角形)
设未知量
解答问题
(构建三角函数模型)
(代入数据求解)
求解方程
数学问题
建立方程
谈
收获
1.知识收获
2.情感升华
课后作业
P21:1、2、3、4
1、数学源于生活
又应用于生活。
2、数学是思维的体操。
同学们,请尽情的舞动吧!
结束寄语
