人教版七年级上册数学1.3.1有理数的加法课件(16张PPT)
文档属性
| 名称 | 人教版七年级上册数学1.3.1有理数的加法课件(16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 422.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 12:17:48 | ||
图片预览




文档简介
(共16张PPT)
1、如果向东走5米记作+5米,
那么向西走3米记作__.
2、已知a=-5,b=+3,
︱a
︳+︱b︱=__
已知a=-5,b=+3,
︱a︱-︱b︱=__
前提诊测
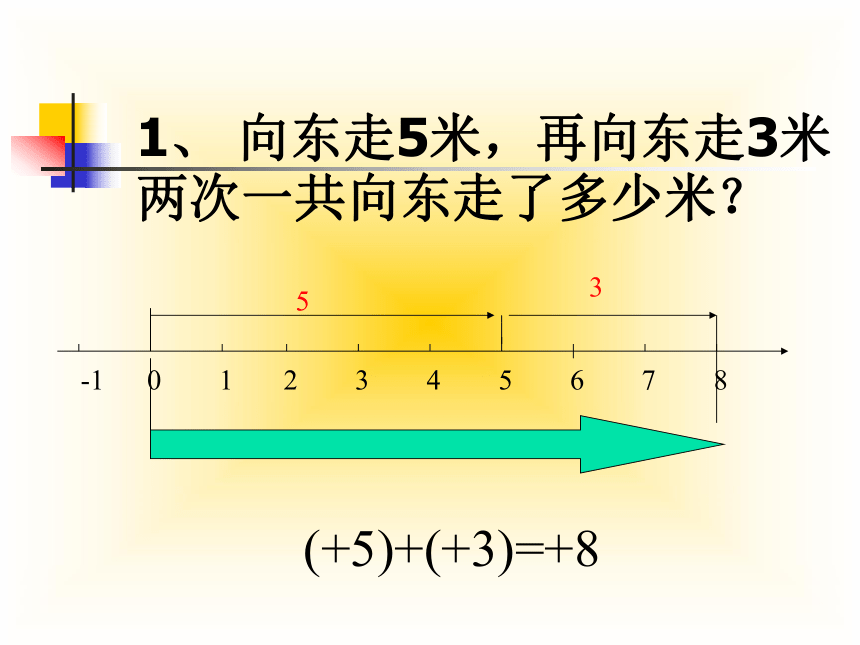
1、
向东走5米,再向东走3米两次一共向东走了多少米?
-1
0
1
2
3
4
5
6
7
8
(+5)+(+3)=+8
5
3
2、向西走5米,再向西走3米两次一共向东走了多少米?
-8
-7
-6
-5
-4
-3
-2
-1
0
1
-
3
-
5
(-5)+(-3)=
-8
3、
向东走5米,再向西走5米,两次一共
向东走了多少米?
(+5)+(-5)=0
-1
0
1
2
3
4
5
6
-
5
5
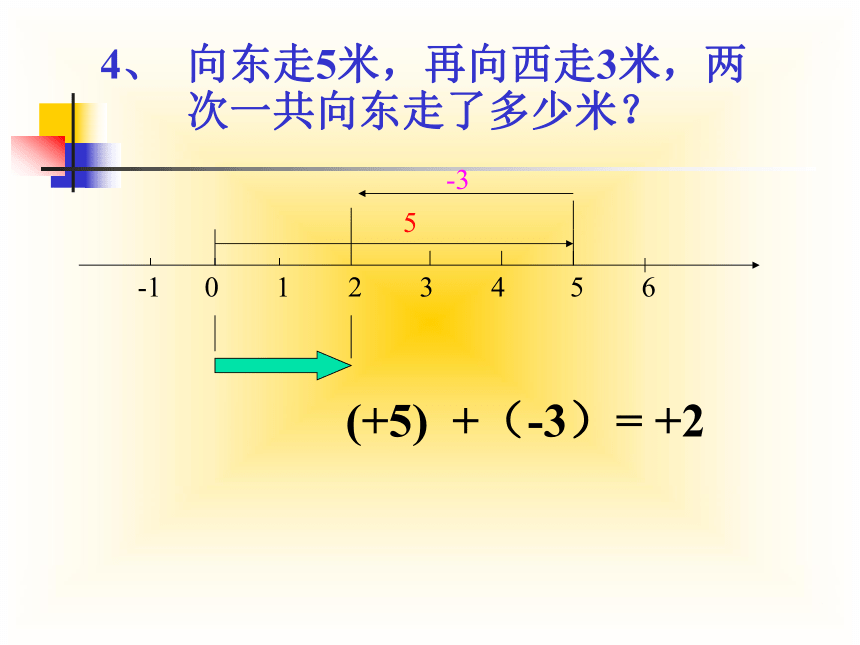
4、
向东走5米,再向西走3米,两
次一共向东走了多少米?
(+5)
+(-3)=
+2
-1
0
1
2
3
4
5
6
5
-3
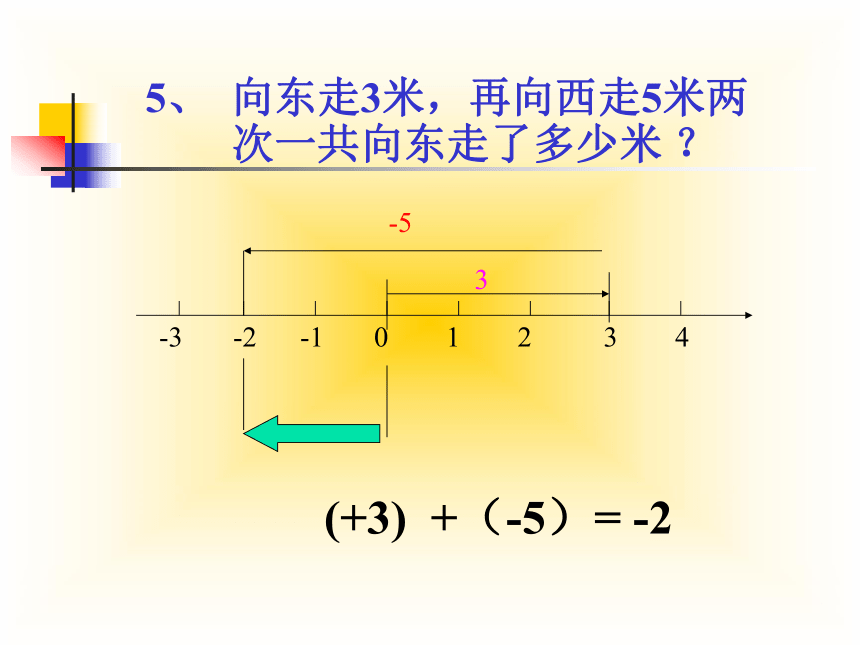
5、
向东走3米,再向西走5米两
次一共向东走了多少米
?
(+3)
+(-5)=
-2
-3
-2
-1
0
1
2
3
4
3
-5
6、
向西走5米,再向东走0米,
两次一共向东走了多少米?
(-5)+
0
=
-5
-5
-4
-3
-2
-1
0
1
-5
同号两数相加:(+5)
+
(+3)
=
+8
(-5)+(-3)=-8
异号两数相加:
+5
+(-3)=
+2
+3
+(-5)=
-2
+5
+(-5)=
0
一数和零相加
(-5)+
0
=
-5
对于上面三种运动结果,我们得到式子:
+3
+(-5)=
-2
+5
+(-5)=
0
(-5)+
5
=
0
思考:
①两个有理数相加,和的符号怎样确定?
②和的数值怎样确定?
③一个有理数同0相加,和是多少?
1、同号两数相加,取相同的符号,并把绝对值相加。
2、绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。互为相反数的两个数相加得0。
3、一个数同0相加,仍得这个数。
有理数加法法则
例如:
(-4)+(-5
)
(同号两数相加)
=-(
)
(取相同的符号)
=-(4
+
5)
(把绝对值相加)
=-
9
(-2)+
6
(绝对值不相等的
异号两数相加)
=+(
)
(取绝对值较大的
加数符号)
=+(6-2)
(用较大的绝对值减去
较小的绝对值)
=
4
练习一
(口答)
1、(+4)+(-7)
2、(-8)+(-3)
3、(-9)+(+5)
4、(-6)+(+6)
5、(-7)+0
6、
8
+(-1)
7、(-7)+1
8、
0+(-10)
(1)
(-3)+(-9)
(2)
(-1/2)+(+1/3)
例:
计算
解:
(1)(-3)+
(-9)
=-(3+9)
=-
12
(2)(-1/2)+(+1/3)=-(1/2-1/3)
=-
1/6
练习二
计算:
(1)
15
+(-22)
(2)(-13)+(-8)
(3)(-0.9)+1.5
(4)
2.7+(-3.5)
(5)
1/2+(-2/3)
(6)(-1/4)+(-1/4)
小结:
1、掌握有理数的加法法则,正确地进
行加法运算。
2、两个有理数相加,首先判断加法类
型,再确定和的符号,最后确定和的绝对值。
1、如果向东走5米记作+5米,
那么向西走3米记作__.
2、已知a=-5,b=+3,
︱a
︳+︱b︱=__
已知a=-5,b=+3,
︱a︱-︱b︱=__
前提诊测
1、
向东走5米,再向东走3米两次一共向东走了多少米?
-1
0
1
2
3
4
5
6
7
8
(+5)+(+3)=+8
5
3
2、向西走5米,再向西走3米两次一共向东走了多少米?
-8
-7
-6
-5
-4
-3
-2
-1
0
1
-
3
-
5
(-5)+(-3)=
-8
3、
向东走5米,再向西走5米,两次一共
向东走了多少米?
(+5)+(-5)=0
-1
0
1
2
3
4
5
6
-
5
5
4、
向东走5米,再向西走3米,两
次一共向东走了多少米?
(+5)
+(-3)=
+2
-1
0
1
2
3
4
5
6
5
-3
5、
向东走3米,再向西走5米两
次一共向东走了多少米
?
(+3)
+(-5)=
-2
-3
-2
-1
0
1
2
3
4
3
-5
6、
向西走5米,再向东走0米,
两次一共向东走了多少米?
(-5)+
0
=
-5
-5
-4
-3
-2
-1
0
1
-5
同号两数相加:(+5)
+
(+3)
=
+8
(-5)+(-3)=-8
异号两数相加:
+5
+(-3)=
+2
+3
+(-5)=
-2
+5
+(-5)=
0
一数和零相加
(-5)+
0
=
-5
对于上面三种运动结果,我们得到式子:
+3
+(-5)=
-2
+5
+(-5)=
0
(-5)+
5
=
0
思考:
①两个有理数相加,和的符号怎样确定?
②和的数值怎样确定?
③一个有理数同0相加,和是多少?
1、同号两数相加,取相同的符号,并把绝对值相加。
2、绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。互为相反数的两个数相加得0。
3、一个数同0相加,仍得这个数。
有理数加法法则
例如:
(-4)+(-5
)
(同号两数相加)
=-(
)
(取相同的符号)
=-(4
+
5)
(把绝对值相加)
=-
9
(-2)+
6
(绝对值不相等的
异号两数相加)
=+(
)
(取绝对值较大的
加数符号)
=+(6-2)
(用较大的绝对值减去
较小的绝对值)
=
4
练习一
(口答)
1、(+4)+(-7)
2、(-8)+(-3)
3、(-9)+(+5)
4、(-6)+(+6)
5、(-7)+0
6、
8
+(-1)
7、(-7)+1
8、
0+(-10)
(1)
(-3)+(-9)
(2)
(-1/2)+(+1/3)
例:
计算
解:
(1)(-3)+
(-9)
=-(3+9)
=-
12
(2)(-1/2)+(+1/3)=-(1/2-1/3)
=-
1/6
练习二
计算:
(1)
15
+(-22)
(2)(-13)+(-8)
(3)(-0.9)+1.5
(4)
2.7+(-3.5)
(5)
1/2+(-2/3)
(6)(-1/4)+(-1/4)
小结:
1、掌握有理数的加法法则,正确地进
行加法运算。
2、两个有理数相加,首先判断加法类
型,再确定和的符号,最后确定和的绝对值。
