湘教版九年级下册数学:1.1 二次函数课件(共16张PPT)
文档属性
| 名称 | 湘教版九年级下册数学:1.1 二次函数课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
情境激疑
美妙的弧线
1.从实际情境中建立两个变量之间的二次函数关系。体验如何用数学方法描述变量之间的数量关系。
2.理解二次函数的概念,掌握二次函数的一般形式。通过观察、操作、交流归纳等数学活动加深对二次函数概念的理解。
学习目标
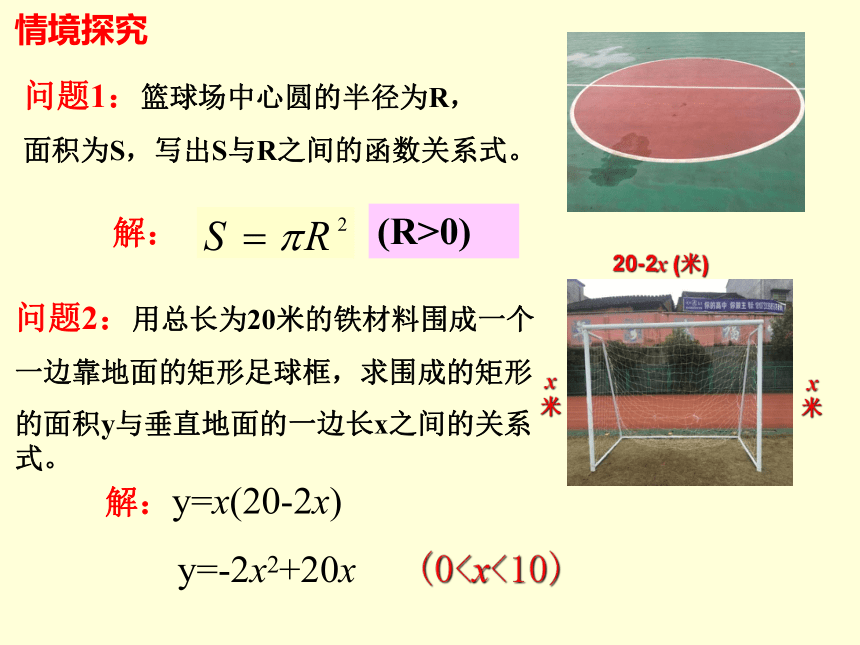
问题1:篮球场中心圆的半径为R,
面积为S,写出S与R之间的函数关系式。
问题2:用总长为20米的铁材料围成一个
一边靠地面的矩形足球框,求围成的矩形
的面积y与垂直地面的一边长x之间的关系式。
x米
20-2x
(米)
x米
情境探究
问题3:随着足球事业的发展,今年株洲校园足球人数已达4000人,年平均增长率为x,预计2019年人数将达y人,写出y关于x的函数关系式。
情境探究
第一年人数:
4000人
第二年人数:
4000(1
+
x)2人
第三年人数:
4000(1
+
x)人
得到的三个函数关系式有什么特点?
温馨提示:分组交流,互相帮助!
(1)右边都是关于x的整式.
(2)自变量x的最高次数是2.
观
察:
y=-2x2+20x
合作解疑
讨论:
1、定义:如果函数解析式是关于自变量的二次多项式,这样的函数叫二次函数。
2、一般形式:y=ax2+bx+c(a、b、c为常数,a≠0)
a为二次项系数,
b为一次项系数,c为常数项。
1.函数表达式为自变量的整式。
2.化简后自变量的最高次数是2。
收获新知
3.二次项系数a不能为0。
二次函数的特殊形式:
(1)当b=0时,
y=ax2+c
(2)当c=0时,
y=ax2+bx
(3)当b=0,c=0时,
y=ax2
快乐砸蛋
1.下列函数中,哪些是二次函数?
1.下列函数中,哪些是二次函数?
1.下列函数中,哪些是二次函数?
快乐砸蛋
是
不是
是
不是
先化简后判断
例1:y=(m+3)x
(1)
m取什么值时,此函数是正比例函数?
(2)
m取什么值时,此函数是反比例函数?
(3)
m取什么值时,此函数是二次函数?
m2-7
小试牛刀
例2:若函数
为二次函数,求m的值。
解:因为该函数为二次函数,
则
解(1)得:m=2或-1
解(2)得:
所以m=2
交流展示
如图,正方形ABCD的边长为1,E、F分别是边BC和CD上的动点(不与正方形的顶点重合),不管E、F怎样动,始终保持AE⊥EF。设BE=x,DF=y,则y是x的函数,函数关系式是( )
A、y=x+1
B、y=x-1
C、y=x2-x+1
D、y=x2-x-1
挑战自我
C
回味无穷
1.定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.其中,是x自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
y=ax?+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax?(a≠0,b=0,c=0,).
(2)y=ax?+c(a≠0,b=0,c≠0).
(3)y=ax?+bx(a≠0,b≠0,c=0).
2.定义的实质是:ax?+bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.
1、m为___时,函数y=(m-1)
是二次函数。
2、已知函数y=(a-2)x2+4x+3不是二次函数,则
=__.
3、已知函数y=(m2-9)x2+(m+3)x+5
是一个一次函数,则2m
=_____
-1
16
8
随堂检测
情境激疑
美妙的弧线
1.从实际情境中建立两个变量之间的二次函数关系。体验如何用数学方法描述变量之间的数量关系。
2.理解二次函数的概念,掌握二次函数的一般形式。通过观察、操作、交流归纳等数学活动加深对二次函数概念的理解。
学习目标
问题1:篮球场中心圆的半径为R,
面积为S,写出S与R之间的函数关系式。
问题2:用总长为20米的铁材料围成一个
一边靠地面的矩形足球框,求围成的矩形
的面积y与垂直地面的一边长x之间的关系式。
x米
20-2x
(米)
x米
情境探究
问题3:随着足球事业的发展,今年株洲校园足球人数已达4000人,年平均增长率为x,预计2019年人数将达y人,写出y关于x的函数关系式。
情境探究
第一年人数:
4000人
第二年人数:
4000(1
+
x)2人
第三年人数:
4000(1
+
x)人
得到的三个函数关系式有什么特点?
温馨提示:分组交流,互相帮助!
(1)右边都是关于x的整式.
(2)自变量x的最高次数是2.
观
察:
y=-2x2+20x
合作解疑
讨论:
1、定义:如果函数解析式是关于自变量的二次多项式,这样的函数叫二次函数。
2、一般形式:y=ax2+bx+c(a、b、c为常数,a≠0)
a为二次项系数,
b为一次项系数,c为常数项。
1.函数表达式为自变量的整式。
2.化简后自变量的最高次数是2。
收获新知
3.二次项系数a不能为0。
二次函数的特殊形式:
(1)当b=0时,
y=ax2+c
(2)当c=0时,
y=ax2+bx
(3)当b=0,c=0时,
y=ax2
快乐砸蛋
1.下列函数中,哪些是二次函数?
1.下列函数中,哪些是二次函数?
1.下列函数中,哪些是二次函数?
快乐砸蛋
是
不是
是
不是
先化简后判断
例1:y=(m+3)x
(1)
m取什么值时,此函数是正比例函数?
(2)
m取什么值时,此函数是反比例函数?
(3)
m取什么值时,此函数是二次函数?
m2-7
小试牛刀
例2:若函数
为二次函数,求m的值。
解:因为该函数为二次函数,
则
解(1)得:m=2或-1
解(2)得:
所以m=2
交流展示
如图,正方形ABCD的边长为1,E、F分别是边BC和CD上的动点(不与正方形的顶点重合),不管E、F怎样动,始终保持AE⊥EF。设BE=x,DF=y,则y是x的函数,函数关系式是( )
A、y=x+1
B、y=x-1
C、y=x2-x+1
D、y=x2-x-1
挑战自我
C
回味无穷
1.定义:一般地,形如y=ax?+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.其中,是x自变量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
y=ax?+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax?(a≠0,b=0,c=0,).
(2)y=ax?+c(a≠0,b=0,c≠0).
(3)y=ax?+bx(a≠0,b≠0,c=0).
2.定义的实质是:ax?+bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.
1、m为___时,函数y=(m-1)
是二次函数。
2、已知函数y=(a-2)x2+4x+3不是二次函数,则
=__.
3、已知函数y=(m2-9)x2+(m+3)x+5
是一个一次函数,则2m
=_____
-1
16
8
随堂检测
