人教版九年级下册数学 课件: 28.2.1 解直角三角形的应用 (共14张)
文档属性
| 名称 | 人教版九年级下册数学 课件: 28.2.1 解直角三角形的应用 (共14张) |

|
|
| 格式 | zip | ||
| 文件大小 | 559.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 00:00:00 | ||
图片预览

文档简介
(共14张PPT)
解直角三角形的应用
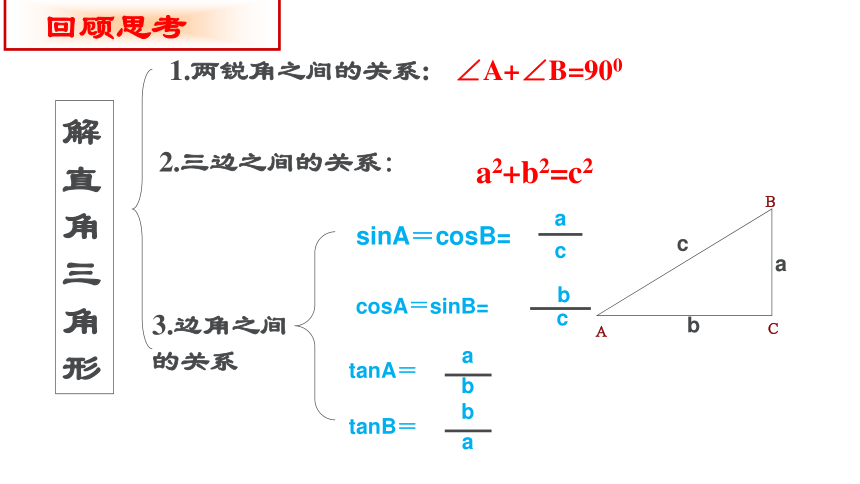
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=900
a2+b2=c2
A
C
B
a
b
c
sinA=cosB=
a
c
cosA=sinB=
b
c
tanA=
a
b
回顾思考
tanB=
b
a
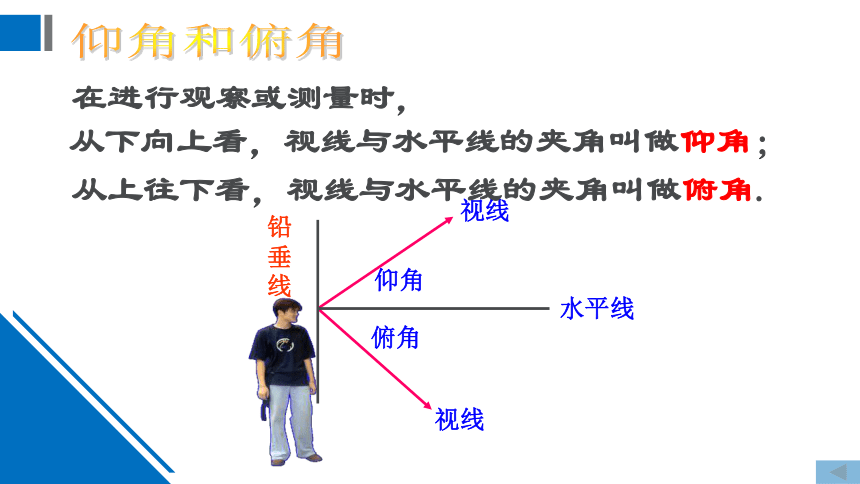
铅垂线
水平线
视线
视线
仰角
俯角
在进行观察或测量时,
仰角和俯角
从上往下看,视线与水平线的夹角叫做俯角.
从下向上看,视线与水平线的夹角叫做仰角;
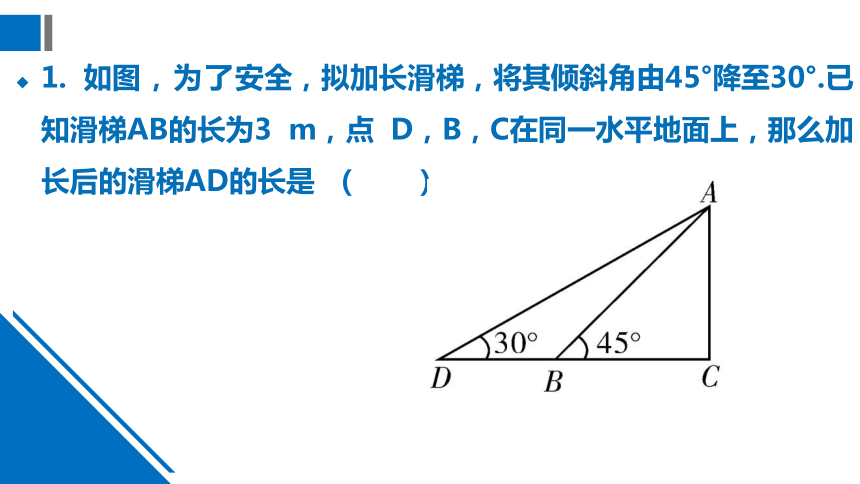
1.
如图,为了安全,拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3
m,点
D,B,C在同一水平地面上,那么加长后的滑梯AD的长是
(
)。
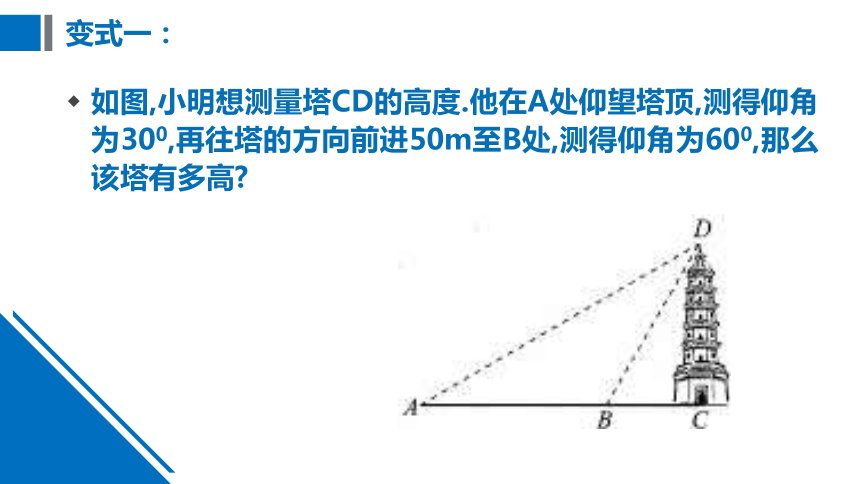
变式一:
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高?
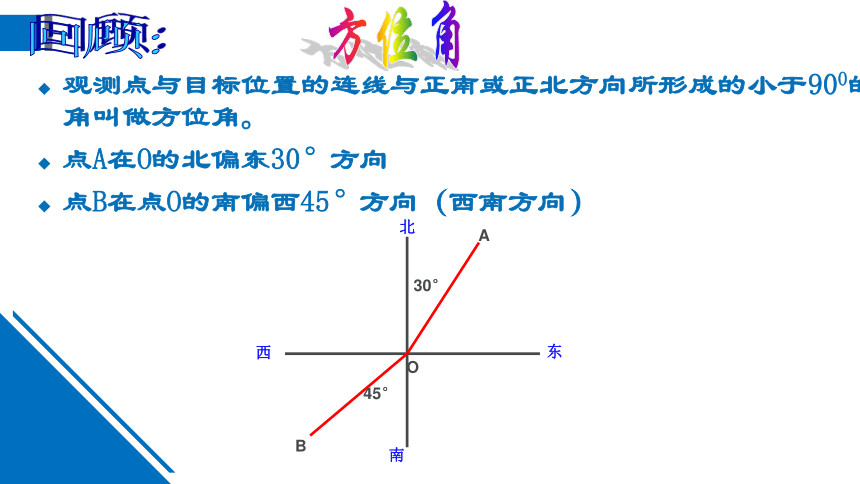
观测点与目标位置的连线与正南或正北方向所形成的小于900的角叫做方位角。
点A在O的北偏东30°方向
点B在点O的南偏西45°方向(西南方向)
30°
45°
B
O
A
东
西
北
南
回顾:
方位角
A
B
D
C
N
N1
24海里
X
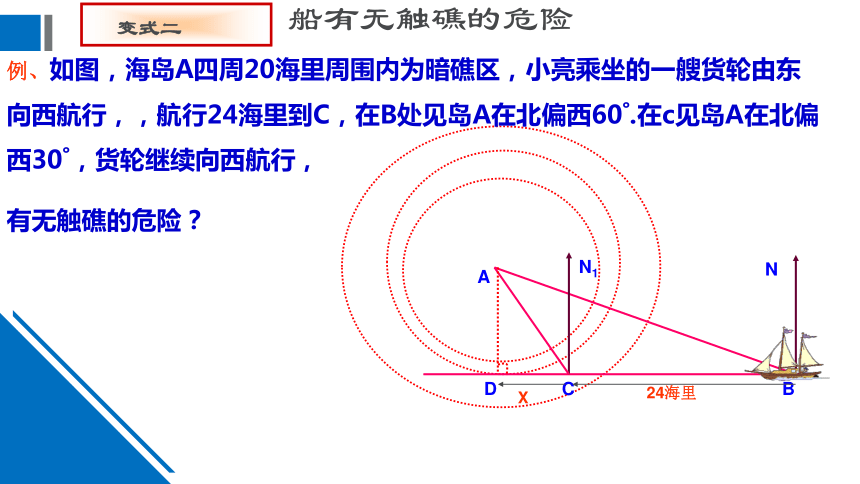
例、如图,海岛A四周20海里周围内为暗礁区,小亮乘坐的一艘货轮由东向西航行,,航行24海里到C,在B处见岛A在北偏西60?.在c见岛A在北偏西30?,货轮继续向西航行,
有无触礁的危险?
船有无触礁的危险
变式二
答:货轮无触礁危险。
在Rt△ADC中,
∵
tan∠DCA=------
∴AD=
tan600x=
x
在Rt△ADB中,
∵
tan30?=
----
=
--------
AD≈12×1.732
=20.784
>
20
解:过点A作AD⊥BC于D,
A
B
D
C
N
N1
24海里
X
AD
DC
AD
BD
3
x
√
X=12
X+24
设CD=x,则BD=X+24
例、如图,海岛A四周20海里周围内为暗礁区,小亮乘坐的一艘货轮由东向西航行,,航行24海里到C,在B处见岛A在北偏西60?.在c见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?
60°
30°
P
B
C
A
80
变式三
如图,在数学活动课中,小敏为了测量旗杆AB的高度,站在教学楼上的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的水平距离CD为9
m,则旗杆的高度是多少?
当堂检测
通过这几道习题你能发现什么?
以4人小组为单位,分享你的发现。
模型一
模型二
我的收获
模型三
试一试
?
悟性的高低取决于有无悟“心”,其实,人与
人的差别就在于你是否去思考,去发现.
解直角三角形的应用
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=900
a2+b2=c2
A
C
B
a
b
c
sinA=cosB=
a
c
cosA=sinB=
b
c
tanA=
a
b
回顾思考
tanB=
b
a
铅垂线
水平线
视线
视线
仰角
俯角
在进行观察或测量时,
仰角和俯角
从上往下看,视线与水平线的夹角叫做俯角.
从下向上看,视线与水平线的夹角叫做仰角;
1.
如图,为了安全,拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3
m,点
D,B,C在同一水平地面上,那么加长后的滑梯AD的长是
(
)。
变式一:
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高?
观测点与目标位置的连线与正南或正北方向所形成的小于900的角叫做方位角。
点A在O的北偏东30°方向
点B在点O的南偏西45°方向(西南方向)
30°
45°
B
O
A
东
西
北
南
回顾:
方位角
A
B
D
C
N
N1
24海里
X
例、如图,海岛A四周20海里周围内为暗礁区,小亮乘坐的一艘货轮由东向西航行,,航行24海里到C,在B处见岛A在北偏西60?.在c见岛A在北偏西30?,货轮继续向西航行,
有无触礁的危险?
船有无触礁的危险
变式二
答:货轮无触礁危险。
在Rt△ADC中,
∵
tan∠DCA=------
∴AD=
tan600x=
x
在Rt△ADB中,
∵
tan30?=
----
=
--------
AD≈12×1.732
=20.784
>
20
解:过点A作AD⊥BC于D,
A
B
D
C
N
N1
24海里
X
AD
DC
AD
BD
3
x
√
X=12
X+24
设CD=x,则BD=X+24
例、如图,海岛A四周20海里周围内为暗礁区,小亮乘坐的一艘货轮由东向西航行,,航行24海里到C,在B处见岛A在北偏西60?.在c见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?
60°
30°
P
B
C
A
80
变式三
如图,在数学活动课中,小敏为了测量旗杆AB的高度,站在教学楼上的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的水平距离CD为9
m,则旗杆的高度是多少?
当堂检测
通过这几道习题你能发现什么?
以4人小组为单位,分享你的发现。
模型一
模型二
我的收获
模型三
试一试
?
悟性的高低取决于有无悟“心”,其实,人与
人的差别就在于你是否去思考,去发现.
