人教版九年级下册数学课件:27.3 位似——在平面直角坐标系中画位似图形(共25张)
文档属性
| 名称 | 人教版九年级下册数学课件:27.3 位似——在平面直角坐标系中画位似图形(共25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
在平面直角坐标系中画位似图形
寄语:数学并不神秘,不是只有天才才能学好数学,只要通过努力,掌握适当的方法,人人都能学会数学。
27.3.2
平面坐标系中的位似
D
E
F
A
O
B
C
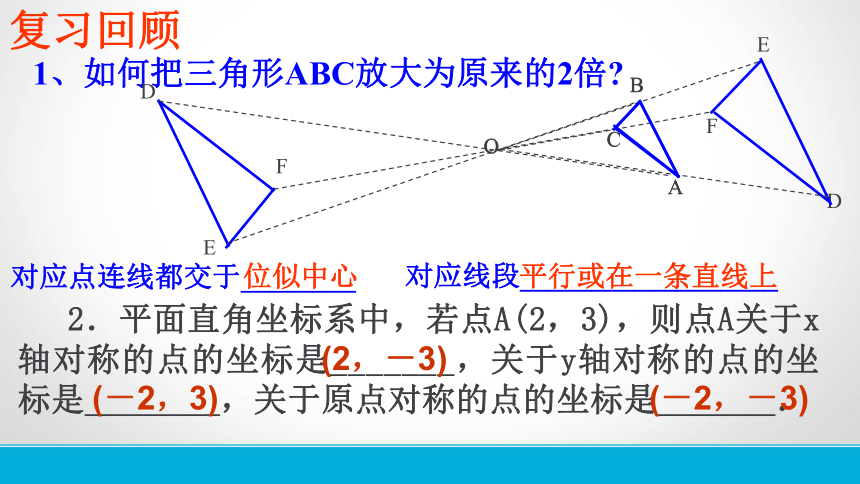
1、如何把三角形ABC放大为原来的2倍?
D
E
F
A
O
B
C
复习回顾
对应点连线都交于________
对应线段__________________
位似中心
平行或在一条直线上
2.平面直角坐标系中,若点A(2,3),则点A关于x轴对称的点的坐标是_______,关于y轴对称的点的坐标是________,关于原点对称的点的坐标是_______.
(2,-3)
(-2,3)
(-2,-3)
1、如果把位似图形放到直角坐标系中,又如何去探究位似变换与坐标之间的关系呢?
接下来想一想?
O
x
y
A(6,3)
5
B(6,0)
A′
B′
③找
的对应点
B″
A″
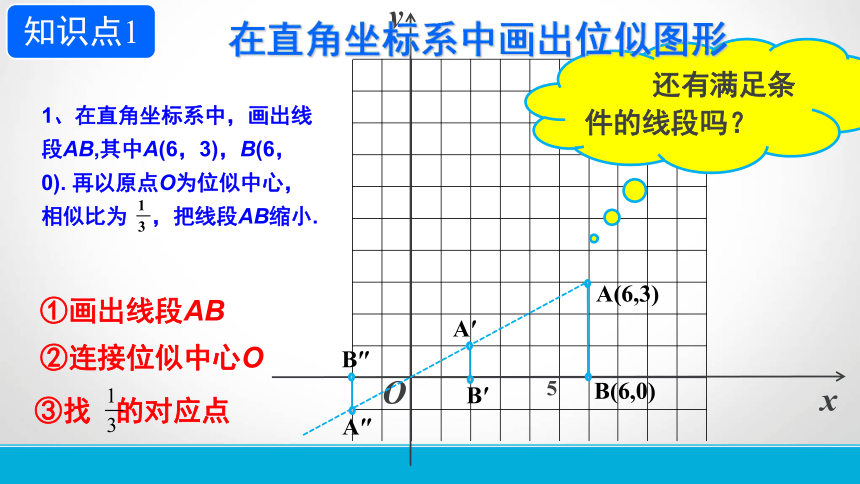
还有满足条件的线段吗?
1、在直角坐标系中,画出线段AB,其中A(6,3),B(6,0).
再以原点O为位似中心,相似比为
,把线段AB缩小.
知识点1
在直角坐标系中画出位似图形
①画出线段AB
②连接位似中心O
O
x
y
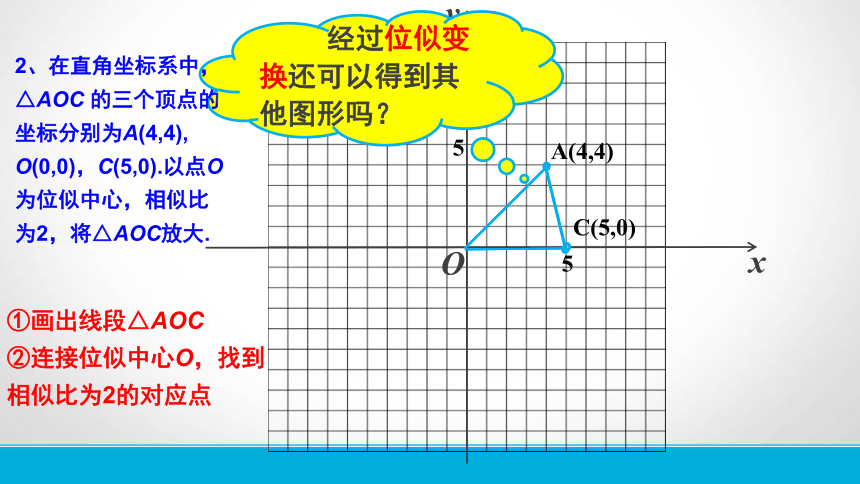
①画出线段△AOC
②连接位似中心O,找到相似比为2的对应点
A(4,4)
C(5,0)
5
5
经过位似变换还可以得到其他图形吗?
2、在直角坐标系中,△AOC
的三个顶点的坐标分别为A(4,4),
O(0,0),C(5,0).以点O为位似中心,相似比为2,将△AOC放大.
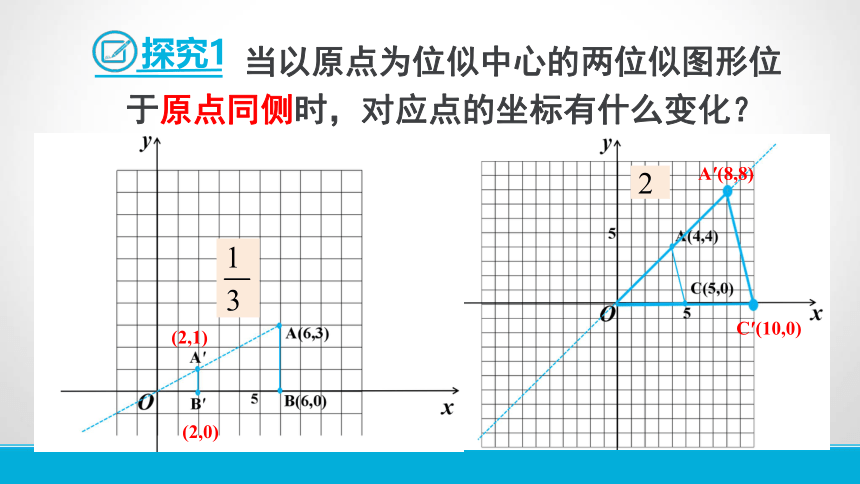
当以原点为位似中心的两位似图形位于原点同侧时,对应点的坐标有什么变化?
探究1
(2,1)
(2,0)
A′(8,8)
C′(10,0)
规律:在平面直角坐标系中,如果以原点为位似中心,新图形与原图形的相似比为k,那么当两图形位于原点同侧时,与原图形上的点(x
,
y)对应的位似图形上的点的坐标是
.
(kx
,
ky)
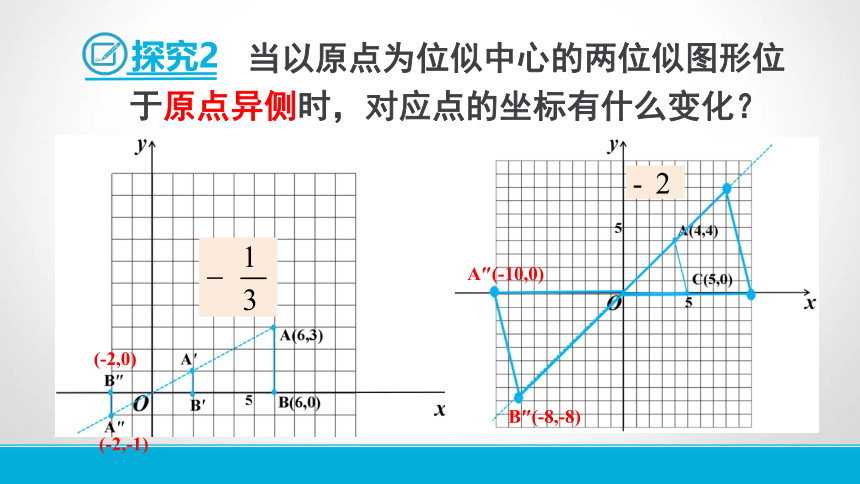
探究2
当以原点为位似中心的两位似图形位于原点异侧时,对应点的坐标有什么变化?
(-2,0)
(-2,-1)
A″(-10,0)
B″(-8,-8)
规律:在平面直角坐标系中,如果以原点为位似中心,新图形与原图形的相似比为k,那么当两图形位于原点异侧时,与原图形上的点(x
,
y)对应的位似图形上的点的坐标是
.
(-kx
,
-ky)
一般地,在平面直角坐标系中,如果以原点为位似中心,新图形与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
位似图形的坐标规律
x
O
y
-2
2
2
4
6
A
B
还可以得到其他图形吗?
A′(-3,6)
B′(-3,0)
A″
B″
典例精析
例
如图,△ABO三个
顶点的坐标分别为
A(-2,4),
B(-2,0),
O(0,0).
以原点O
为位似中心,
画出一个
三角形,
使它与△ABO
的相似比为
.
1.如图表示△AOB和把它缩小后得到的△OCD,求△AOB与△COD的相似比。
解:相似比为OB:OD=5:2.
A
B
5
5
C
D
练习
2.如图,△ABO三个顶点的坐标分别为A(4,-5),
B(6,0),
O(0,0).
以原点O为位似中心,把这个三角形放大为原来的2倍,得到△A′B′O′.写出△A′B′O′三个顶点的坐标.
6
-5
A
B
6
-5
A
B
A(4,-5),
B(6,0)
A′(8,-10),
B′(12,0)
A″(-8,10),
B″(-12,0)
至此,我们已经学习了平移、轴对称、旋转和位似等图形的变化方式.你能在下图所示的图案中找到它们吗?
平移、轴对称、旋转、位似变换的坐标变化规律
平移变换
轴对称变换
旋转变换
位似变换
对应点的横坐标或纵坐标加上(或减去)平移的单位长度
以x
轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以y
轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数
一个图形绕原点旋转180°
,则旋转前后两个图形对应点的横坐标与纵坐标都互为相反数
当以原点为位似中心时,变换前后两个图形对应点的横坐标、纵坐标之比的绝对值等于相似比
随堂演练
基础巩固
1.某学习小组在讨论“变化的鱼”时,
知道大鱼与小鱼是位似图形(如图所示),
则小鱼上的点(a,
b)对应大鱼上的点(
)
A.(-2a,
-2b)
B.(-a,
-2b)
C.(-2b,
-2a)
D.(-2a,
-b)
A
2.△ABC三个顶点坐标分别为A(-2,-2),B(-4,-2),C(-6,-4),以原点为位似中心,将△ABC放大后得到的△DEF与△ABC的相似比为2∶1,这时△DEF中点D的坐标是
.
(-4,-4)或(4,4)
综合应用
如图所示,
图中的小方格都是边长为1的正方形,
△ABC与△A′B′C′是以O为位似中心的位似图形,
它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)直接写出△ABC与△A′B′C′
的相似比;
相似比为2∶1
x
y
O
6
12
(3)以位似中心O为坐标原点,
以格线所在直线为坐标轴建立平面直角坐标系,
画出△A′B′C′关于点O
中心对称的△A″B″C″,
并直接写出△A″B″C″各顶点的坐标.
x
y
O
6
12
A″(6,0),
B″(3,-2),
C″(4,-4).
课堂小结
目前已经学了哪些变换?有什么区别与联系?
平移、轴对称、旋转
还有
位似变换
位似与平移、轴对称、旋转三种变换的联系和区别:
联系:位似、平移、轴对称、旋转都是图形变换的基本形式;
区别:平移、轴对称、旋转三种图形变换都是全等变换,而位似变换是相似(扩大或缩小)变换.
若
①以原点为位似中心;
②新图形与原图形的相似比为k;
③原图形上的点(x,y);
则对应的位似图形上的点的坐标为
(kx,ky)或(-kx,-ky).
坐标系中的位似变换规律:
寄语:愿同学们在人生的坐标系中,以知识为位似中心,放大梦想,缩小困难,用数学知识画出精彩的图形!
在平面直角坐标系中画位似图形
寄语:数学并不神秘,不是只有天才才能学好数学,只要通过努力,掌握适当的方法,人人都能学会数学。
27.3.2
平面坐标系中的位似
D
E
F
A
O
B
C
1、如何把三角形ABC放大为原来的2倍?
D
E
F
A
O
B
C
复习回顾
对应点连线都交于________
对应线段__________________
位似中心
平行或在一条直线上
2.平面直角坐标系中,若点A(2,3),则点A关于x轴对称的点的坐标是_______,关于y轴对称的点的坐标是________,关于原点对称的点的坐标是_______.
(2,-3)
(-2,3)
(-2,-3)
1、如果把位似图形放到直角坐标系中,又如何去探究位似变换与坐标之间的关系呢?
接下来想一想?
O
x
y
A(6,3)
5
B(6,0)
A′
B′
③找
的对应点
B″
A″
还有满足条件的线段吗?
1、在直角坐标系中,画出线段AB,其中A(6,3),B(6,0).
再以原点O为位似中心,相似比为
,把线段AB缩小.
知识点1
在直角坐标系中画出位似图形
①画出线段AB
②连接位似中心O
O
x
y
①画出线段△AOC
②连接位似中心O,找到相似比为2的对应点
A(4,4)
C(5,0)
5
5
经过位似变换还可以得到其他图形吗?
2、在直角坐标系中,△AOC
的三个顶点的坐标分别为A(4,4),
O(0,0),C(5,0).以点O为位似中心,相似比为2,将△AOC放大.
当以原点为位似中心的两位似图形位于原点同侧时,对应点的坐标有什么变化?
探究1
(2,1)
(2,0)
A′(8,8)
C′(10,0)
规律:在平面直角坐标系中,如果以原点为位似中心,新图形与原图形的相似比为k,那么当两图形位于原点同侧时,与原图形上的点(x
,
y)对应的位似图形上的点的坐标是
.
(kx
,
ky)
探究2
当以原点为位似中心的两位似图形位于原点异侧时,对应点的坐标有什么变化?
(-2,0)
(-2,-1)
A″(-10,0)
B″(-8,-8)
规律:在平面直角坐标系中,如果以原点为位似中心,新图形与原图形的相似比为k,那么当两图形位于原点异侧时,与原图形上的点(x
,
y)对应的位似图形上的点的坐标是
.
(-kx
,
-ky)
一般地,在平面直角坐标系中,如果以原点为位似中心,新图形与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
位似图形的坐标规律
x
O
y
-2
2
2
4
6
A
B
还可以得到其他图形吗?
A′(-3,6)
B′(-3,0)
A″
B″
典例精析
例
如图,△ABO三个
顶点的坐标分别为
A(-2,4),
B(-2,0),
O(0,0).
以原点O
为位似中心,
画出一个
三角形,
使它与△ABO
的相似比为
.
1.如图表示△AOB和把它缩小后得到的△OCD,求△AOB与△COD的相似比。
解:相似比为OB:OD=5:2.
A
B
5
5
C
D
练习
2.如图,△ABO三个顶点的坐标分别为A(4,-5),
B(6,0),
O(0,0).
以原点O为位似中心,把这个三角形放大为原来的2倍,得到△A′B′O′.写出△A′B′O′三个顶点的坐标.
6
-5
A
B
6
-5
A
B
A(4,-5),
B(6,0)
A′(8,-10),
B′(12,0)
A″(-8,10),
B″(-12,0)
至此,我们已经学习了平移、轴对称、旋转和位似等图形的变化方式.你能在下图所示的图案中找到它们吗?
平移、轴对称、旋转、位似变换的坐标变化规律
平移变换
轴对称变换
旋转变换
位似变换
对应点的横坐标或纵坐标加上(或减去)平移的单位长度
以x
轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以y
轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数
一个图形绕原点旋转180°
,则旋转前后两个图形对应点的横坐标与纵坐标都互为相反数
当以原点为位似中心时,变换前后两个图形对应点的横坐标、纵坐标之比的绝对值等于相似比
随堂演练
基础巩固
1.某学习小组在讨论“变化的鱼”时,
知道大鱼与小鱼是位似图形(如图所示),
则小鱼上的点(a,
b)对应大鱼上的点(
)
A.(-2a,
-2b)
B.(-a,
-2b)
C.(-2b,
-2a)
D.(-2a,
-b)
A
2.△ABC三个顶点坐标分别为A(-2,-2),B(-4,-2),C(-6,-4),以原点为位似中心,将△ABC放大后得到的△DEF与△ABC的相似比为2∶1,这时△DEF中点D的坐标是
.
(-4,-4)或(4,4)
综合应用
如图所示,
图中的小方格都是边长为1的正方形,
△ABC与△A′B′C′是以O为位似中心的位似图形,
它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)直接写出△ABC与△A′B′C′
的相似比;
相似比为2∶1
x
y
O
6
12
(3)以位似中心O为坐标原点,
以格线所在直线为坐标轴建立平面直角坐标系,
画出△A′B′C′关于点O
中心对称的△A″B″C″,
并直接写出△A″B″C″各顶点的坐标.
x
y
O
6
12
A″(6,0),
B″(3,-2),
C″(4,-4).
课堂小结
目前已经学了哪些变换?有什么区别与联系?
平移、轴对称、旋转
还有
位似变换
位似与平移、轴对称、旋转三种变换的联系和区别:
联系:位似、平移、轴对称、旋转都是图形变换的基本形式;
区别:平移、轴对称、旋转三种图形变换都是全等变换,而位似变换是相似(扩大或缩小)变换.
若
①以原点为位似中心;
②新图形与原图形的相似比为k;
③原图形上的点(x,y);
则对应的位似图形上的点的坐标为
(kx,ky)或(-kx,-ky).
坐标系中的位似变换规律:
寄语:愿同学们在人生的坐标系中,以知识为位似中心,放大梦想,缩小困难,用数学知识画出精彩的图形!
