湘教版九年级下册数学课件:2.4 过不共线三点作圆(共17张)
文档属性
| 名称 | 湘教版九年级下册数学课件:2.4 过不共线三点作圆(共17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
2.4
过不共线三点作圆
湘教版
九年级下册
第2章
圆
长沙马王堆一号汉墓的发掘,在我国的考古界算得上惊人的发现,在世界考古学史上,也产生了深远的影响。一位考古学家在马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家将这个破损的圆形瓷器复原,以便于进行深入的研究吗?
学习了今天的新课,你就知道该怎样做了。
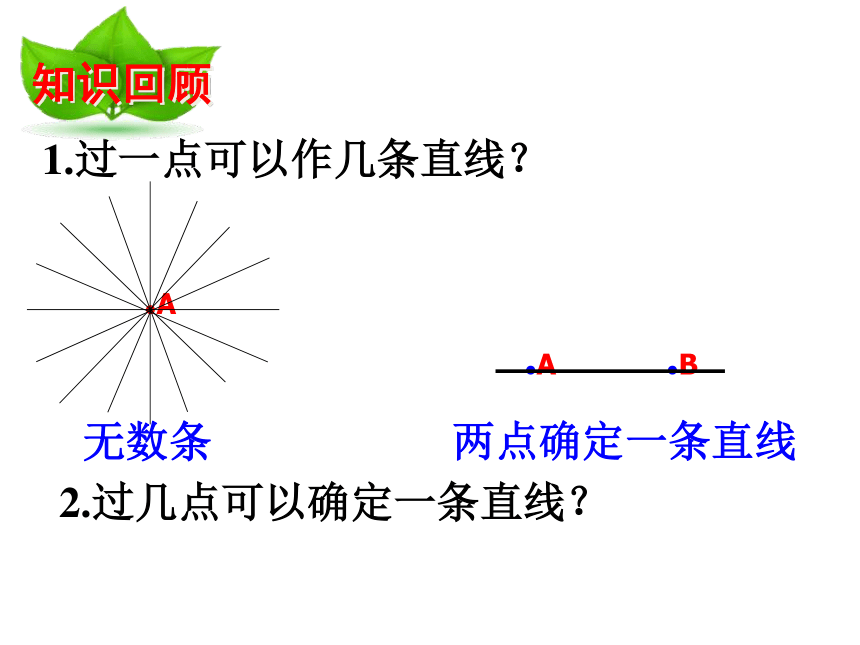
1.过一点可以作几条直线?
2.过几点可以确定一条直线?
●A
●A
●B
无数条
两点确定一条直线
请思考下列问题:
1、作一个圆的关键是什么?
2、线段垂直平分线的性质与判定是什么?
3、过一个点可以作几个圆,过两点可以作几个圆,那么过三点呢?
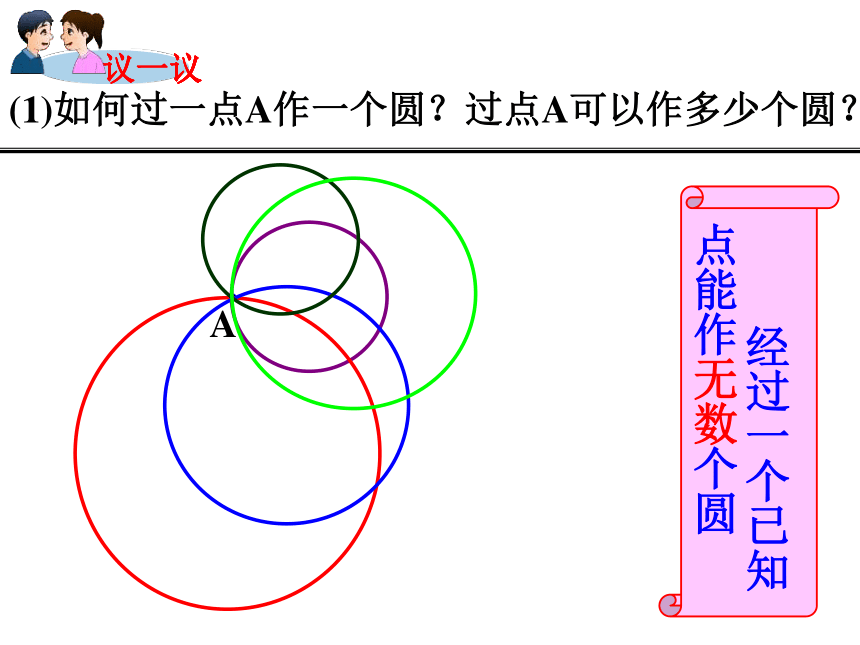
(1)如何过一点A作一个圆?过点A可以作多少个圆?
A
经过一个已知点能作无数个圆
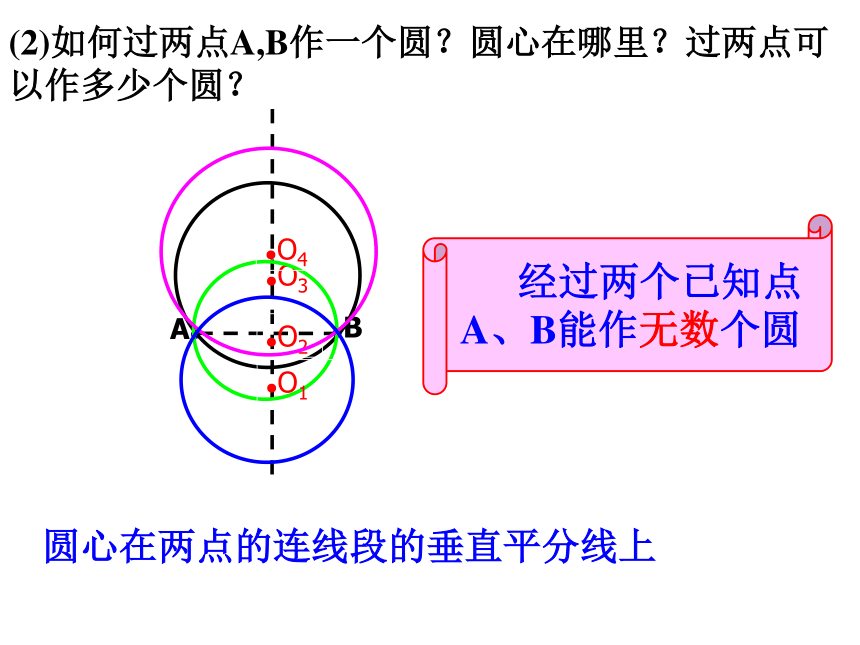
经过两个已知点A、B能作无数个圆
A●
●B
(2)如何过两点A,B作一个圆?圆心在哪里?过两点可以作多少个圆?
圆心在两点的连线段的垂直平分线上
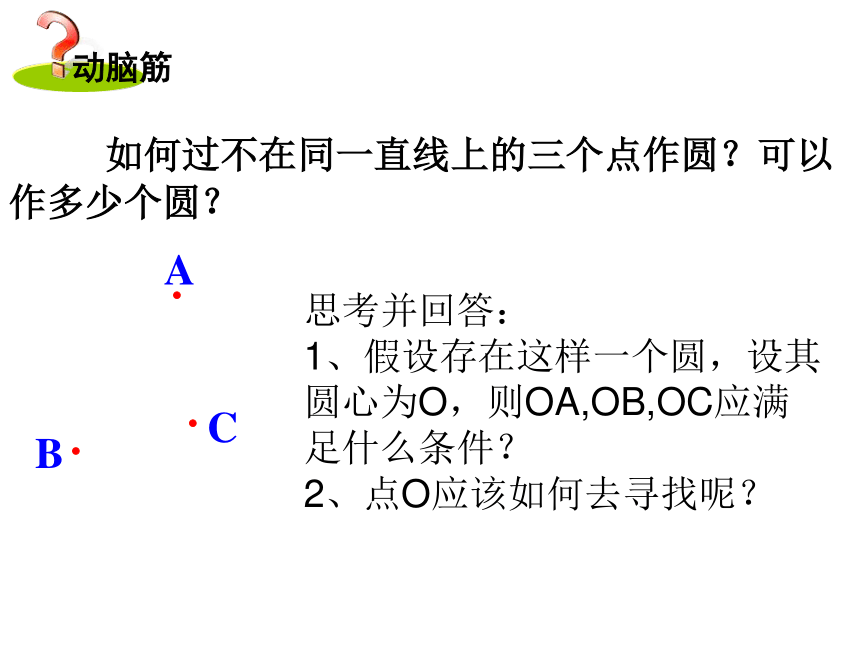
如何过不在同一直线上的三个点作圆?可以作多少个圆?
思考并回答:
1、假设存在这样一个圆,设其圆心为O,则OA,OB,OC应满足什么条件?
2、点O应该如何去寻找呢?
已知:不在同一直线上的三点A、B、C.
求作:
⊙O,使它经过点A、B、C.
3.以O为圆心,OA为半径作圆。
O
E
F
N
M
A
B
C
作法:
1.连结AB,作线段AB的垂直
平分线EF;
2.连接AC,作线段AC的垂直
平分线MN,交EF于点O;
则⊙O就是所求作的圆。
∟
∟
过不在同一直线上的三点有且只可以作一个圆.
由此可以得出什么结论?
A
B
C
过在同一直线上的三点A,B,C可以作一个圆吗?
∟
∟
不可以
现在你知道了怎样要将一个如图所示的破损的圆盘复原了吗?
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OA长为半径作圆。
因此⊙O即为所求的圆。
A
B
C
O
经过△ABC的三个顶点可以作一个圆吗?
●O
通过图形,能不能说出三角形的外接圆,三角形的外心,圆的内接三角形的有关概念?
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
如图:
⊙O是△ABC的外接圆,
点O是△ABC的外心,
△ABC是⊙O的内接三角形。
思考下列问题:
1、如何作三角形的外心?
2、三角形的外心有何性质?
结论:三角形的外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离都等于半径。
分别作出锐角三角形、直角三角形、钝角三角形外心,观察他们的位置有何不同。
三角形的外心位置
锐角三角形的外心位于三角形的内部.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形的外部.
三角形的外心位置
某一个城市在一块空地新建了三个居民小区,它
们分别为A、B、C,且三个小区不在同一直线上,
要想规划一所中学,使这所中学到三个小区的距
离相等。请问同学们这所中学建在哪个位置?你
怎么确定这个位置呢?
●
●
●
B
A
C
1.通过本课的学习,你有什么收获?还有什么问题?
2.确定圆的条件——
不在同一直线上的三点
圆心、半径
3.
锐角三角形
在三角形的内部
直角三角形
--外心的位置---
在斜边上
钝角三角形
在三角形的外部
2.4
过不共线三点作圆
湘教版
九年级下册
第2章
圆
长沙马王堆一号汉墓的发掘,在我国的考古界算得上惊人的发现,在世界考古学史上,也产生了深远的影响。一位考古学家在马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家将这个破损的圆形瓷器复原,以便于进行深入的研究吗?
学习了今天的新课,你就知道该怎样做了。
1.过一点可以作几条直线?
2.过几点可以确定一条直线?
●A
●A
●B
无数条
两点确定一条直线
请思考下列问题:
1、作一个圆的关键是什么?
2、线段垂直平分线的性质与判定是什么?
3、过一个点可以作几个圆,过两点可以作几个圆,那么过三点呢?
(1)如何过一点A作一个圆?过点A可以作多少个圆?
A
经过一个已知点能作无数个圆
经过两个已知点A、B能作无数个圆
A●
●B
(2)如何过两点A,B作一个圆?圆心在哪里?过两点可以作多少个圆?
圆心在两点的连线段的垂直平分线上
如何过不在同一直线上的三个点作圆?可以作多少个圆?
思考并回答:
1、假设存在这样一个圆,设其圆心为O,则OA,OB,OC应满足什么条件?
2、点O应该如何去寻找呢?
已知:不在同一直线上的三点A、B、C.
求作:
⊙O,使它经过点A、B、C.
3.以O为圆心,OA为半径作圆。
O
E
F
N
M
A
B
C
作法:
1.连结AB,作线段AB的垂直
平分线EF;
2.连接AC,作线段AC的垂直
平分线MN,交EF于点O;
则⊙O就是所求作的圆。
∟
∟
过不在同一直线上的三点有且只可以作一个圆.
由此可以得出什么结论?
A
B
C
过在同一直线上的三点A,B,C可以作一个圆吗?
∟
∟
不可以
现在你知道了怎样要将一个如图所示的破损的圆盘复原了吗?
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OA长为半径作圆。
因此⊙O即为所求的圆。
A
B
C
O
经过△ABC的三个顶点可以作一个圆吗?
●O
通过图形,能不能说出三角形的外接圆,三角形的外心,圆的内接三角形的有关概念?
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
如图:
⊙O是△ABC的外接圆,
点O是△ABC的外心,
△ABC是⊙O的内接三角形。
思考下列问题:
1、如何作三角形的外心?
2、三角形的外心有何性质?
结论:三角形的外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离都等于半径。
分别作出锐角三角形、直角三角形、钝角三角形外心,观察他们的位置有何不同。
三角形的外心位置
锐角三角形的外心位于三角形的内部.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形的外部.
三角形的外心位置
某一个城市在一块空地新建了三个居民小区,它
们分别为A、B、C,且三个小区不在同一直线上,
要想规划一所中学,使这所中学到三个小区的距
离相等。请问同学们这所中学建在哪个位置?你
怎么确定这个位置呢?
●
●
●
B
A
C
1.通过本课的学习,你有什么收获?还有什么问题?
2.确定圆的条件——
不在同一直线上的三点
圆心、半径
3.
锐角三角形
在三角形的内部
直角三角形
--外心的位置---
在斜边上
钝角三角形
在三角形的外部
