初中数学人教版七年级数学上3.4 实际问题与一元一次方程 课件(共48张PPT)
文档属性
| 名称 | 初中数学人教版七年级数学上3.4 实际问题与一元一次方程 课件(共48张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 13:27:30 | ||
图片预览









文档简介
(共48张PPT)
第三章
一元一次方程
3.4
实际问题与一元一次方程
①相遇问题:
甲走的路程+乙走的路程
=甲乙两出发地的路程
练1:甲乙两地相距230千米,一辆卡车和一辆客车分别以50千米/小时和40千米/小时的速度从两地出发,相向而行,若卡车早出发1小时,则问客车出发后几小时两车相遇?
卡车后行
230千米
客车行的路程
卡车先行
相遇
卡车先行的S+后行的S+客车行驶的S=230千米
解:设客车出发后
小时两车相遇。
答:客车出发后2小时两车相遇。
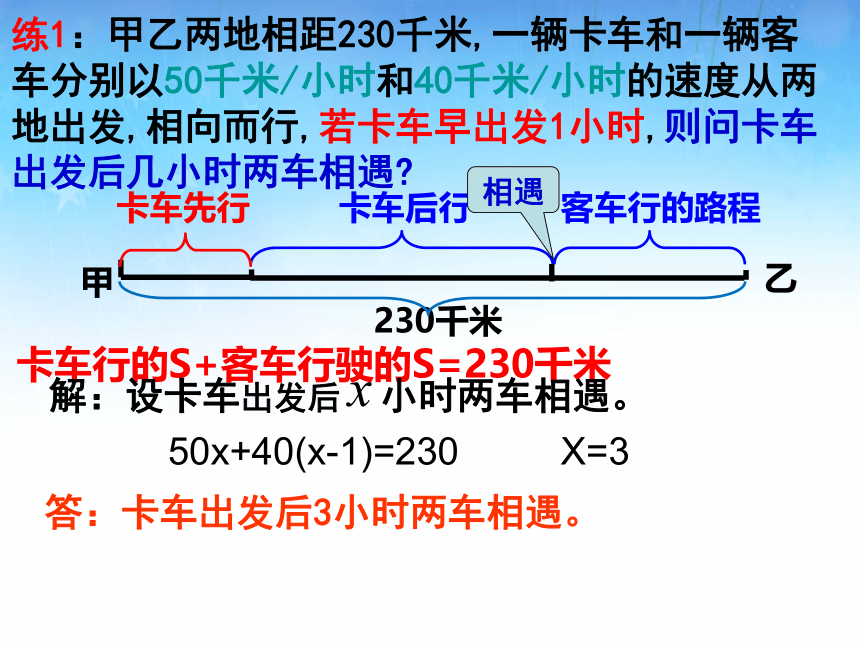
练1:甲乙两地相距230千米,一辆卡车和一辆客车分别以50千米/小时和40千米/小时的速度从两地出发,相向而行,若卡车早出发1小时,则问卡车出发后几小时两车相遇?
卡车后行
230千米
客车行的路程
卡车先行
相遇
卡车行的S+客车行驶的S=230千米
解:设卡车出发后
小时两车相遇。
答:卡车出发后3小时两车相遇。
50x+40(x-1)=230
X=3
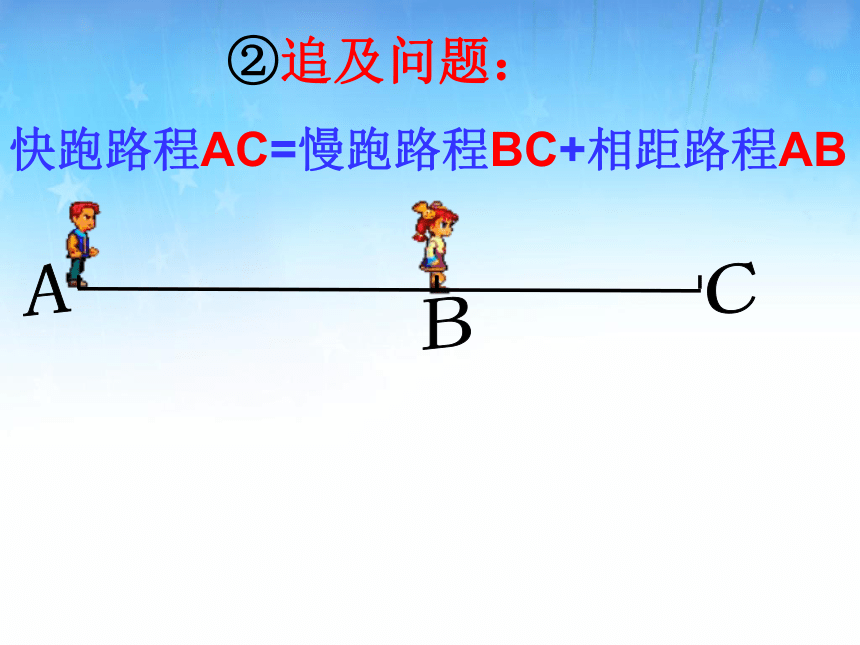
②追及问题:
快跑路程AC=慢跑路程BC+相距路程AB
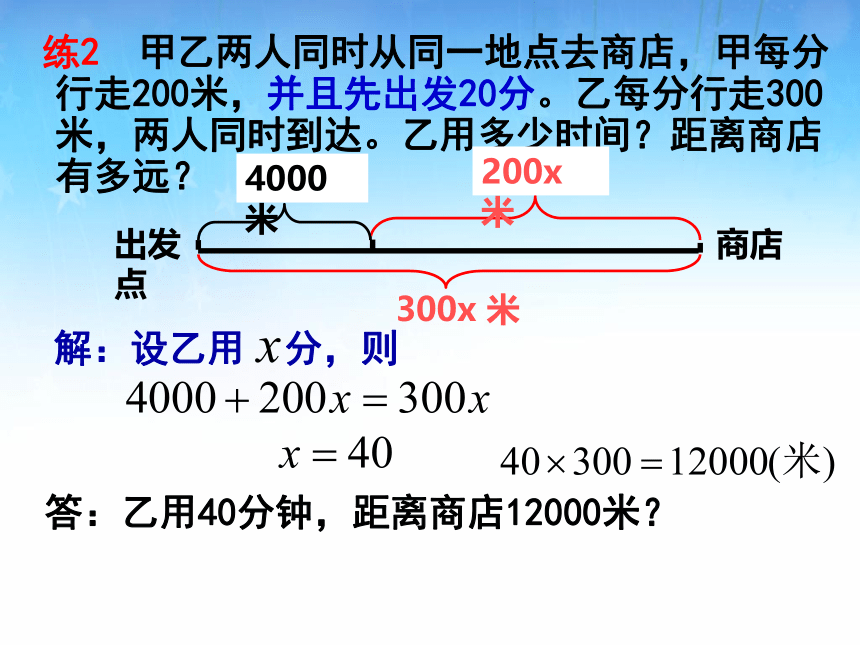
练2 甲乙两人同时从同一地点去商店,甲每分行走200米,并且先出发20分。乙每分行走300米,两人同时到达。乙用多少时间?距离商店有多远?
解:设乙用
分,则
答:乙用40分钟,距离商店12000米?
300x
米
4000米
200x
米
练2:甲乙两人同时从同一地点去商店,甲每分行走200米,并且先出发20分。乙每分行走300米,两人同时到达。甲用多少时间?距离商店有多远?
乙走(x-20)分
甲先走20分钟
甲后走(x-20)分
解设甲用了X分
200x=300(x-20)
X=60
答:甲用60分钟,距离商店12000米?
某人计划骑车以每小时12千米的速度由A地到B地,这样便可在规定的时间到达B地,但他因事将原计划的时间推迟了20分,便只好以每小时15千米的速度前进,结果比规定时间早4分钟到达B地,求A、B两地间的距离。
设由A地到B地规定的时间是
x
小时
12x=
方法二:设由A、B两地的距离是
x
千米
甲、乙两人同时从A地前往相距25.5千米的B地,甲骑自行车,乙步行,甲的速度比乙的速度的2倍还快2千米/时,甲先到达B地后,立即由B地返回,在途中遇到乙,这时距他们出发时已过了3小时。求两人的速度。
解:设乙的速度是
x
千米/时,则
3x+3
(2x+2)=25.5×2
航行问题:
飞机的飞行
顺风飞行
逆风飞行
轮船的航行:
顺水航行
逆水航行
速度关系:
逆水速度=船在静水中的速度-水速
顺水速度=船在静水中的速度+水速
逆风速度=在无风中的速度-风速
顺风速度=在无风中的速度+风速
例1:
一条船在两个码头之间航行。顺水时需要4.5小时,逆水返回需要5小时20分钟,水流速度是1千米/时,这两个码头相距多少千米?
一轮船往返于甲乙两码头,顺水航行需要3小时,逆水航行比顺水航行多45分钟。若轮船在静水中的速度为每小时24千米,求水流速度。
例2.一小船由A顺流到B需行驶6小时,由B逆流到A需行驶8小时,一天,小船由A顺流到达B发现一救生圈中途落水,立即返回,1小时后找到救生圈,若水流速度是2千米/时。
(1)小船在静水中的速度是多少?
(2)救生圈是何时掉入水中的?
某船从A码头顺流航行到B码头,然后逆流返行到C码头,共行20小时,已知船在静水中的速度为7.5千米/时,水流的速度为2.5千米/时,若A与C的距离比A与B的距离短40千米,求A与B的距离。
解:设A与B的距离是x千米
②
当C在BA的延长线上时
解得x=120
解得x=56
答:A与B的距离是120千米或56千米。
①
当C在A、B之间时
乙
甲
乙
甲
环形背向相遇问题
环形同向相遇问题
例3
甲、乙两人在400米的环形跑道上散步,甲每分钟走110米,乙每分钟走90米,两人同时从一个地点出发,几分钟后两人第一次相遇?
分析:在环形跑道上运动,分两种情况:
已知:V甲〉V乙
图一所示实为
问题
相遇
图二所示实为
问题
追击
甲乙程和=周长
快的路程-慢的路程=周长
第10次相遇呢?
总结:在环形跑道上运动,分两种情况:
甲的行程+乙的行程=跑道的周长
(2)同向而行:
甲的行程-乙的行程=跑道的周长
想一想
若把上题中的“第一次”相遇改为“第二次”
相遇需要时间又是多少呢?若改为“第n次”相遇呢?
(1)背向而行:
甲、乙两人在6千米的环形跑道上竞走,甲的速度是乙的速度7/5倍,从同一地出发同向而行,经35分钟后,他们第一次相遇。问甲、乙两人的速度是多少?
分析:在环形跑道上运动,相向而行,
第一次相遇时,速度快者比速度慢者
恰好多走了一圈。
例4:在钟表面上两点到三点之间,什么
时候分针和时针重合?
分析:用追及问题来解决来问题。
分针走的度数—时针走的=差距
6x-0.5x=60
解:设分针与时针重合需要x分
5.5x=60
练习:
在3点钟和4点钟之间,钟表上的
时针和分针什么时间重合?
3
12
1
2
6
5
4
分针走的度数—时针走的=差距
6x-0.5x=90
解:设分针与时针重合需要x分
5.5x=90
措车问题:
游行队伍在大街上以每小时3千米的速度前进,一个骑自行车的人以每小时15千米的速度向游行队伍迎面驶来,他从队头骑到队尾用去2分钟,求游行队伍的长度。
算术法:
人走路程+队伍走的路程=队伍的长
措车问题:
游行队伍在大街上以每小时3千米的速度前进,一个骑自行车的人以每小时15千米的速度向游行队伍迎面驶来,游行队伍的长度为600米,求他从队头骑到队尾用的时间?
同向措车问题:
长为600米的游行队伍在大街上以每小时3千米的速度前进,第二队伍以每小时15千米的速度同向来行驶,该游行队伍的长度为300米,求第二队从队头接触到队尾离开所用的时间?
相向措车问题:
长为600米的游行队伍在大街上以每小时3千米的速度前进,第二队伍以每小时15千米的速度迎面行驶,该游行队伍的长度为300米,求两队从队头接触到队尾离开所用的时间?
与铁路平行的一条公路上有一行人与骑自行车的人同时向南行进。行人的速度是每小时3.6km,骑自行车的人的速度是每小时10.8km。如果一列火车从他们背后开来,它通过行人的时间是22秒,通过骑自行车的人的时间是26秒。⑴
行人的速度为每秒多少米?
⑵
这列火车的车长是多少米?
等量关系:
①
两种情形下火车的速度相等
②
两种情形下火车的车长相等
在时间已知的情况下,设速度列路程等式的方程,设路程列速度等式的方程。
解:⑴
行人的速度是:3.6km/时=3600米÷3600秒=1米/秒
骑自行车的人的速度是:10.8km/时=10800米÷3600秒=3米/秒
⑵
方法一:设火车的速度是x米/秒,则
26×(x-3)=22×(x-1)
解得x=4
方法二:设火车的车长是x米,则
工程问题
工程问题中的数量关系:
1)
工作效率=
2)工作总量=工作效率×工作时间
3)工作时间=
4)各队合作工作效率=各队工作效率之和
5)全部工作量之和=各队工作量之和
例
修筑一条公路,甲工程队单独承包要80天完成,乙工程队单独承包要120天完成
1)现在由两个工程队合作承包,几天可以完成?
2)如果甲、乙两工程队合作了30天后,因甲工作队另有任务,
剩下工作由乙工作队完成,则修好这条公路共需要几天?
解:
1)设两工程队合作需要x天完成。
2)设修好这条公路共需要
y
天完成。
等量关系:
甲30天工作量+乙队y天的工作量
=
1
答:两工程队合作需要48天完成,修好这条公路还需75天。
等量关系:甲工作量+乙工作量=1
依题意得
依题意得
y=75
x=48
一件工作,甲独做15天完成,乙独做30天完成,甲先做5天之后乙又做了10天,剩余工作由甲、乙二人合作完成,需几天?
某工厂计划26小时生产一批零件,后因每小时多生产5件,用24小时,不但完成了任务,而
且还比原计划多生产了60件,问原计划生产多少零件?
利息问题
例
:小明的爸爸前年存了年利率为2.43%的两年期定期储蓄。今
年到期后,扣除利息税20%,所得利息正好为小明买了一个价值48.6元的计算器,问小明爸爸前年存了多少钱?
解:设小明爸爸前年存了x元。
依题意得:2
×
2.43%x
(1-
20%)=
48.6
x
=
1250
答:小明爸爸前年存了1250元钱
等量关系:利息-利息税=应得利息
利息
=
本金
×
年利率
×
期数
利息税
=
本金
×
年利率
×
期数×税率(20%)
利息问题
练习:某公司存入银行甲、乙两种不同性质的存款共20万元。甲种存款的年利率为1.4%,乙种存款的年利率为3.7%,该公司一年共得利息6250元,求甲、乙两种存款各多少元?
解:设甲种存款为x万元。则乙种存款为(20
-
x)万元
根据题意得:
解方程得:
x
=
5
所以
20
–
x
=
15
答:甲种存款为5万元,乙种存款为15万元
调配问题
例:某部队开展支农活动,甲队27人,乙队19人,现另调26人去支援,使甲队是乙队的2倍,问应调往甲队、乙队各多少人?
解:设调往甲队x人,则调往乙队(26-x)人
根据题意,得方程:
解方程得:x
=
21
答:调往甲队21人。调往乙队5人。
甲、乙两车间各有工人若干,如果从乙车间调100人到甲车间,那么甲车间的人数是乙车间剩余人数的6倍;如果从甲车间调100人到乙车间,这时两车间的人数相等,求原来甲乙车间的人数。
配套问题
等量关系式:
生产出来的两种产品总量成比例
例:包装厂有工人42人,每个工人平均每小时可以生产圆形铁片120片,或长方形铁片80片,将两张圆形铁片与和一张长方形铁片可配套成一个密封圆桶,问如何安排工人生产圆形或长方形铁片能合理地将铁片配套?
某车间有28名工人生产螺栓和螺母,每人每小时平均能生产螺栓12个或螺母18个,应如何分配生产螺栓和螺母的工人,才能使螺栓和螺母正好配套(一个螺栓配两个螺母)?
机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮与3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?
日历数字问题
例1:日历中2×2方块的四个数的和是72,求这四个数。
解:设四个数中最小的数为x,
解方程,得:x
=
14
答:这四个数分别为14,15,21,22。
例2:一个两位数,个位数字与十位数字的和是11,若交换十位数字与个位数字的位置,则新数比原数小9,求原两位数。
练习
1、一个两位数,十位数与个位上的数字之和为11,如果把十位上的数字与个位上的数字对调,那么得到的数比原来的数大63,求原来的两位数?
2、一个两位数,十位上的数比个位上的数小1,十位上与个位上的数字之和为这个数的,求这个两位数?
市场经济问题
市场经济问题
一家商店将某种服装按进价提高40%后标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的进价是多少?
某商店开张为吸引顾客,所有商品一律按八折优惠出售,已知某种旅游鞋每双进价为60元,八折出售后,商家所获利润率为40%。问这种鞋的标价是多少元?优惠价是多少?
工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.该工艺品每件的进价、标价分别是多少元?
某高校共有5个大餐厅和2个小餐厅.经过测试:同时开放1个大餐厅、2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅、1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅、1个小餐厅分别可供多少名学生就餐;
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由.
典型例题
例1:小明家的灯泡坏了,去商店买,现有两种灯泡可供选择,其中一种是10瓦(即0.01千瓦)的节能灯,售价是60元;另一种是60瓦(即0.06千瓦)的白炽灯,两种灯的照明效果一样,使用寿命都可以达到3000小时,节能灯售价高,但是较省电;白炽灯售价低,但是用电多,如果电费的单价是0.5元/千瓦时,选哪种灯可以节省费用(灯的售价加电费)?
解析:
1、问题中的基本等量关系有哪些?
(1)总费用=灯的售价+
;
(2)电费=灯的千瓦数×
×
。
2、列式表示费用:
设照明时间是t小时,则节能灯的费用=
;
白炽灯的费用=
。
3、哪一种灯的费用低呢?用特殊值验证一下。
当t=2000时,节能灯的费用=
;白炽灯的费用=
。当t=2500时,节能灯的费用=
;白炽灯的费用=
。
4、照明多少小时用这两种灯的费用相等?
5、如果计划照明时间3500小时,则需要购买两个灯,试设计你认为能省钱的选灯方案。
练习:
1、某牛奶厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元;制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获取利润2000元;该工厂的生产能力是:如果制成酸奶,每天可加工3吨;制成奶片,每天可加工1吨,受人员限制,两种加工方式不能同时进行;受气温限制,这批牛奶必须在4天内全部销售或加工完毕。为此,该厂设计了两种方案,方案一:尽可能多地制成奶片,其余的直接销售鲜奶;方案二:将一部分制成奶片,其余的制成酸奶销售,并恰好4天完成,你认为选择哪种方案获利多呢?
解:方案一:尽可能多地做奶片,可做
吨,获利
元。
方案二:设x天生产奶片,则
天生产酸奶,列方程得
。
解得x=
。∴生产奶片
吨,生产酸奶
吨,共获利
元。
(或设x吨鲜奶制成奶片,则其余
吨鲜奶制成酸奶,列方程得
。解得x=
。∴共获利
元。)
∵
,
∴
。
2、某市百货商店元月一日搞促销活动,购物不超过200元不给优惠;超过200元,而不足500元按9折优惠;超过500元,其中500元按9折优惠,超过部分按8折优惠,某人两次购物分别用了134元和466元,
问:(1)此人两次购物,其所购物品打折前是多少钱?
(2)在此活动中,他节省了多少钱?
(3)若此人将两次购物的钱合起来购相同的商品,能省
钱吗?说明你的理由。
第三章
一元一次方程
3.4
实际问题与一元一次方程
①相遇问题:
甲走的路程+乙走的路程
=甲乙两出发地的路程
练1:甲乙两地相距230千米,一辆卡车和一辆客车分别以50千米/小时和40千米/小时的速度从两地出发,相向而行,若卡车早出发1小时,则问客车出发后几小时两车相遇?
卡车后行
230千米
客车行的路程
卡车先行
相遇
卡车先行的S+后行的S+客车行驶的S=230千米
解:设客车出发后
小时两车相遇。
答:客车出发后2小时两车相遇。
练1:甲乙两地相距230千米,一辆卡车和一辆客车分别以50千米/小时和40千米/小时的速度从两地出发,相向而行,若卡车早出发1小时,则问卡车出发后几小时两车相遇?
卡车后行
230千米
客车行的路程
卡车先行
相遇
卡车行的S+客车行驶的S=230千米
解:设卡车出发后
小时两车相遇。
答:卡车出发后3小时两车相遇。
50x+40(x-1)=230
X=3
②追及问题:
快跑路程AC=慢跑路程BC+相距路程AB
练2 甲乙两人同时从同一地点去商店,甲每分行走200米,并且先出发20分。乙每分行走300米,两人同时到达。乙用多少时间?距离商店有多远?
解:设乙用
分,则
答:乙用40分钟,距离商店12000米?
300x
米
4000米
200x
米
练2:甲乙两人同时从同一地点去商店,甲每分行走200米,并且先出发20分。乙每分行走300米,两人同时到达。甲用多少时间?距离商店有多远?
乙走(x-20)分
甲先走20分钟
甲后走(x-20)分
解设甲用了X分
200x=300(x-20)
X=60
答:甲用60分钟,距离商店12000米?
某人计划骑车以每小时12千米的速度由A地到B地,这样便可在规定的时间到达B地,但他因事将原计划的时间推迟了20分,便只好以每小时15千米的速度前进,结果比规定时间早4分钟到达B地,求A、B两地间的距离。
设由A地到B地规定的时间是
x
小时
12x=
方法二:设由A、B两地的距离是
x
千米
甲、乙两人同时从A地前往相距25.5千米的B地,甲骑自行车,乙步行,甲的速度比乙的速度的2倍还快2千米/时,甲先到达B地后,立即由B地返回,在途中遇到乙,这时距他们出发时已过了3小时。求两人的速度。
解:设乙的速度是
x
千米/时,则
3x+3
(2x+2)=25.5×2
航行问题:
飞机的飞行
顺风飞行
逆风飞行
轮船的航行:
顺水航行
逆水航行
速度关系:
逆水速度=船在静水中的速度-水速
顺水速度=船在静水中的速度+水速
逆风速度=在无风中的速度-风速
顺风速度=在无风中的速度+风速
例1:
一条船在两个码头之间航行。顺水时需要4.5小时,逆水返回需要5小时20分钟,水流速度是1千米/时,这两个码头相距多少千米?
一轮船往返于甲乙两码头,顺水航行需要3小时,逆水航行比顺水航行多45分钟。若轮船在静水中的速度为每小时24千米,求水流速度。
例2.一小船由A顺流到B需行驶6小时,由B逆流到A需行驶8小时,一天,小船由A顺流到达B发现一救生圈中途落水,立即返回,1小时后找到救生圈,若水流速度是2千米/时。
(1)小船在静水中的速度是多少?
(2)救生圈是何时掉入水中的?
某船从A码头顺流航行到B码头,然后逆流返行到C码头,共行20小时,已知船在静水中的速度为7.5千米/时,水流的速度为2.5千米/时,若A与C的距离比A与B的距离短40千米,求A与B的距离。
解:设A与B的距离是x千米
②
当C在BA的延长线上时
解得x=120
解得x=56
答:A与B的距离是120千米或56千米。
①
当C在A、B之间时
乙
甲
乙
甲
环形背向相遇问题
环形同向相遇问题
例3
甲、乙两人在400米的环形跑道上散步,甲每分钟走110米,乙每分钟走90米,两人同时从一个地点出发,几分钟后两人第一次相遇?
分析:在环形跑道上运动,分两种情况:
已知:V甲〉V乙
图一所示实为
问题
相遇
图二所示实为
问题
追击
甲乙程和=周长
快的路程-慢的路程=周长
第10次相遇呢?
总结:在环形跑道上运动,分两种情况:
甲的行程+乙的行程=跑道的周长
(2)同向而行:
甲的行程-乙的行程=跑道的周长
想一想
若把上题中的“第一次”相遇改为“第二次”
相遇需要时间又是多少呢?若改为“第n次”相遇呢?
(1)背向而行:
甲、乙两人在6千米的环形跑道上竞走,甲的速度是乙的速度7/5倍,从同一地出发同向而行,经35分钟后,他们第一次相遇。问甲、乙两人的速度是多少?
分析:在环形跑道上运动,相向而行,
第一次相遇时,速度快者比速度慢者
恰好多走了一圈。
例4:在钟表面上两点到三点之间,什么
时候分针和时针重合?
分析:用追及问题来解决来问题。
分针走的度数—时针走的=差距
6x-0.5x=60
解:设分针与时针重合需要x分
5.5x=60
练习:
在3点钟和4点钟之间,钟表上的
时针和分针什么时间重合?
3
12
1
2
6
5
4
分针走的度数—时针走的=差距
6x-0.5x=90
解:设分针与时针重合需要x分
5.5x=90
措车问题:
游行队伍在大街上以每小时3千米的速度前进,一个骑自行车的人以每小时15千米的速度向游行队伍迎面驶来,他从队头骑到队尾用去2分钟,求游行队伍的长度。
算术法:
人走路程+队伍走的路程=队伍的长
措车问题:
游行队伍在大街上以每小时3千米的速度前进,一个骑自行车的人以每小时15千米的速度向游行队伍迎面驶来,游行队伍的长度为600米,求他从队头骑到队尾用的时间?
同向措车问题:
长为600米的游行队伍在大街上以每小时3千米的速度前进,第二队伍以每小时15千米的速度同向来行驶,该游行队伍的长度为300米,求第二队从队头接触到队尾离开所用的时间?
相向措车问题:
长为600米的游行队伍在大街上以每小时3千米的速度前进,第二队伍以每小时15千米的速度迎面行驶,该游行队伍的长度为300米,求两队从队头接触到队尾离开所用的时间?
与铁路平行的一条公路上有一行人与骑自行车的人同时向南行进。行人的速度是每小时3.6km,骑自行车的人的速度是每小时10.8km。如果一列火车从他们背后开来,它通过行人的时间是22秒,通过骑自行车的人的时间是26秒。⑴
行人的速度为每秒多少米?
⑵
这列火车的车长是多少米?
等量关系:
①
两种情形下火车的速度相等
②
两种情形下火车的车长相等
在时间已知的情况下,设速度列路程等式的方程,设路程列速度等式的方程。
解:⑴
行人的速度是:3.6km/时=3600米÷3600秒=1米/秒
骑自行车的人的速度是:10.8km/时=10800米÷3600秒=3米/秒
⑵
方法一:设火车的速度是x米/秒,则
26×(x-3)=22×(x-1)
解得x=4
方法二:设火车的车长是x米,则
工程问题
工程问题中的数量关系:
1)
工作效率=
2)工作总量=工作效率×工作时间
3)工作时间=
4)各队合作工作效率=各队工作效率之和
5)全部工作量之和=各队工作量之和
例
修筑一条公路,甲工程队单独承包要80天完成,乙工程队单独承包要120天完成
1)现在由两个工程队合作承包,几天可以完成?
2)如果甲、乙两工程队合作了30天后,因甲工作队另有任务,
剩下工作由乙工作队完成,则修好这条公路共需要几天?
解:
1)设两工程队合作需要x天完成。
2)设修好这条公路共需要
y
天完成。
等量关系:
甲30天工作量+乙队y天的工作量
=
1
答:两工程队合作需要48天完成,修好这条公路还需75天。
等量关系:甲工作量+乙工作量=1
依题意得
依题意得
y=75
x=48
一件工作,甲独做15天完成,乙独做30天完成,甲先做5天之后乙又做了10天,剩余工作由甲、乙二人合作完成,需几天?
某工厂计划26小时生产一批零件,后因每小时多生产5件,用24小时,不但完成了任务,而
且还比原计划多生产了60件,问原计划生产多少零件?
利息问题
例
:小明的爸爸前年存了年利率为2.43%的两年期定期储蓄。今
年到期后,扣除利息税20%,所得利息正好为小明买了一个价值48.6元的计算器,问小明爸爸前年存了多少钱?
解:设小明爸爸前年存了x元。
依题意得:2
×
2.43%x
(1-
20%)=
48.6
x
=
1250
答:小明爸爸前年存了1250元钱
等量关系:利息-利息税=应得利息
利息
=
本金
×
年利率
×
期数
利息税
=
本金
×
年利率
×
期数×税率(20%)
利息问题
练习:某公司存入银行甲、乙两种不同性质的存款共20万元。甲种存款的年利率为1.4%,乙种存款的年利率为3.7%,该公司一年共得利息6250元,求甲、乙两种存款各多少元?
解:设甲种存款为x万元。则乙种存款为(20
-
x)万元
根据题意得:
解方程得:
x
=
5
所以
20
–
x
=
15
答:甲种存款为5万元,乙种存款为15万元
调配问题
例:某部队开展支农活动,甲队27人,乙队19人,现另调26人去支援,使甲队是乙队的2倍,问应调往甲队、乙队各多少人?
解:设调往甲队x人,则调往乙队(26-x)人
根据题意,得方程:
解方程得:x
=
21
答:调往甲队21人。调往乙队5人。
甲、乙两车间各有工人若干,如果从乙车间调100人到甲车间,那么甲车间的人数是乙车间剩余人数的6倍;如果从甲车间调100人到乙车间,这时两车间的人数相等,求原来甲乙车间的人数。
配套问题
等量关系式:
生产出来的两种产品总量成比例
例:包装厂有工人42人,每个工人平均每小时可以生产圆形铁片120片,或长方形铁片80片,将两张圆形铁片与和一张长方形铁片可配套成一个密封圆桶,问如何安排工人生产圆形或长方形铁片能合理地将铁片配套?
某车间有28名工人生产螺栓和螺母,每人每小时平均能生产螺栓12个或螺母18个,应如何分配生产螺栓和螺母的工人,才能使螺栓和螺母正好配套(一个螺栓配两个螺母)?
机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮与3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?
日历数字问题
例1:日历中2×2方块的四个数的和是72,求这四个数。
解:设四个数中最小的数为x,
解方程,得:x
=
14
答:这四个数分别为14,15,21,22。
例2:一个两位数,个位数字与十位数字的和是11,若交换十位数字与个位数字的位置,则新数比原数小9,求原两位数。
练习
1、一个两位数,十位数与个位上的数字之和为11,如果把十位上的数字与个位上的数字对调,那么得到的数比原来的数大63,求原来的两位数?
2、一个两位数,十位上的数比个位上的数小1,十位上与个位上的数字之和为这个数的,求这个两位数?
市场经济问题
市场经济问题
一家商店将某种服装按进价提高40%后标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的进价是多少?
某商店开张为吸引顾客,所有商品一律按八折优惠出售,已知某种旅游鞋每双进价为60元,八折出售后,商家所获利润率为40%。问这种鞋的标价是多少元?优惠价是多少?
工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.该工艺品每件的进价、标价分别是多少元?
某高校共有5个大餐厅和2个小餐厅.经过测试:同时开放1个大餐厅、2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅、1个小餐厅,可供2280名学生就餐.
(1)求1个大餐厅、1个小餐厅分别可供多少名学生就餐;
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由.
典型例题
例1:小明家的灯泡坏了,去商店买,现有两种灯泡可供选择,其中一种是10瓦(即0.01千瓦)的节能灯,售价是60元;另一种是60瓦(即0.06千瓦)的白炽灯,两种灯的照明效果一样,使用寿命都可以达到3000小时,节能灯售价高,但是较省电;白炽灯售价低,但是用电多,如果电费的单价是0.5元/千瓦时,选哪种灯可以节省费用(灯的售价加电费)?
解析:
1、问题中的基本等量关系有哪些?
(1)总费用=灯的售价+
;
(2)电费=灯的千瓦数×
×
。
2、列式表示费用:
设照明时间是t小时,则节能灯的费用=
;
白炽灯的费用=
。
3、哪一种灯的费用低呢?用特殊值验证一下。
当t=2000时,节能灯的费用=
;白炽灯的费用=
。当t=2500时,节能灯的费用=
;白炽灯的费用=
。
4、照明多少小时用这两种灯的费用相等?
5、如果计划照明时间3500小时,则需要购买两个灯,试设计你认为能省钱的选灯方案。
练习:
1、某牛奶厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元;制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获取利润2000元;该工厂的生产能力是:如果制成酸奶,每天可加工3吨;制成奶片,每天可加工1吨,受人员限制,两种加工方式不能同时进行;受气温限制,这批牛奶必须在4天内全部销售或加工完毕。为此,该厂设计了两种方案,方案一:尽可能多地制成奶片,其余的直接销售鲜奶;方案二:将一部分制成奶片,其余的制成酸奶销售,并恰好4天完成,你认为选择哪种方案获利多呢?
解:方案一:尽可能多地做奶片,可做
吨,获利
元。
方案二:设x天生产奶片,则
天生产酸奶,列方程得
。
解得x=
。∴生产奶片
吨,生产酸奶
吨,共获利
元。
(或设x吨鲜奶制成奶片,则其余
吨鲜奶制成酸奶,列方程得
。解得x=
。∴共获利
元。)
∵
,
∴
。
2、某市百货商店元月一日搞促销活动,购物不超过200元不给优惠;超过200元,而不足500元按9折优惠;超过500元,其中500元按9折优惠,超过部分按8折优惠,某人两次购物分别用了134元和466元,
问:(1)此人两次购物,其所购物品打折前是多少钱?
(2)在此活动中,他节省了多少钱?
(3)若此人将两次购物的钱合起来购相同的商品,能省
钱吗?说明你的理由。
