冀教版七下数学9.1三角形的边教学课件(25张ppt)
文档属性
| 名称 | 冀教版七下数学9.1三角形的边教学课件(25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
三角形的边
观察思考:以下的图中,都出现了什么几何图形?这种几何图形有什么特点?如何定义它?
如何定义三角形?
由3条不在同一直线上的线段,首尾顺次相接组成的图形叫做三角形.
三角形的定义
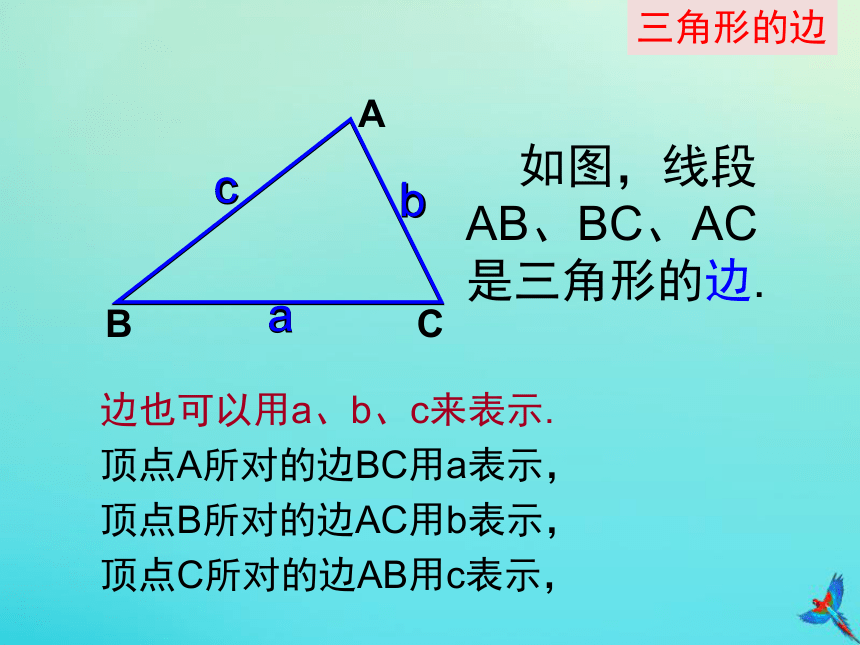
如图,线段AB、BC、AC是三角形的边.
b
c
a
边也可以用a、b、c来表示.
顶点A所对的边BC用a表示,
顶点B所对的边AC用b表示,
顶点C所对的边AB用c表示,
三角形的边
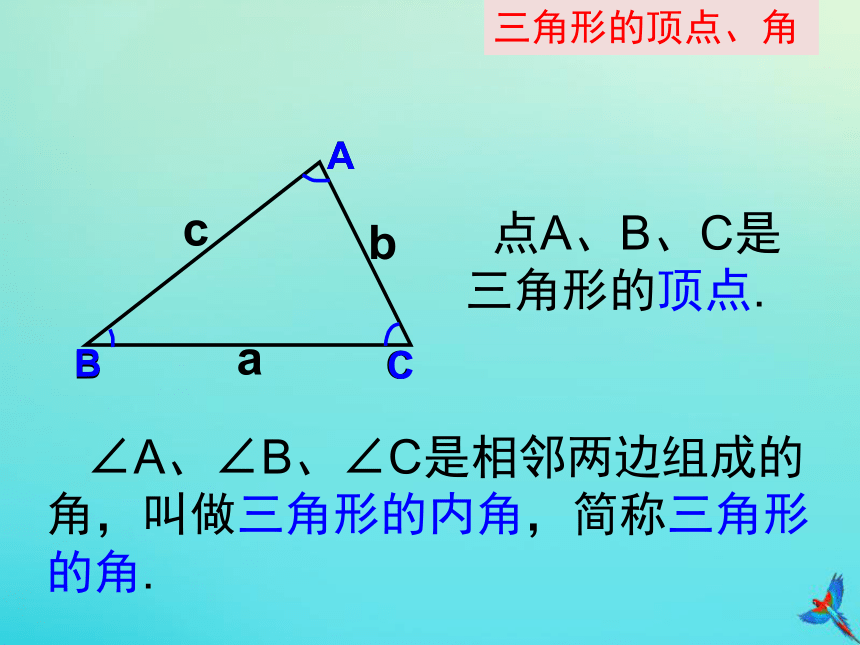
∠A、∠B、∠C是相邻两边组成的角,叫做三角形的内角,简称三角形的角.
点A、B、C是三角形的顶点.
C
A
B
三角形的顶点、角
在
ABC中,AB边所对的角是:
∠A所对的边是:
∠C
BC
★再说几个对边与对角的关系试试.
△ABC
△OPQ
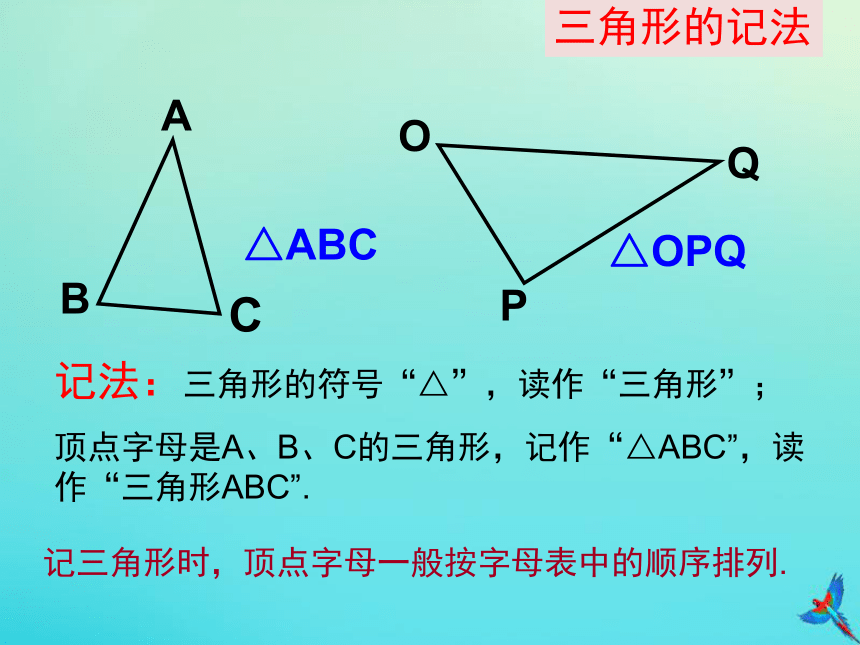
记法:三角形的符号“△”,读作“三角形”;
顶点字母是A、B、C的三角形,记作“△ABC”,读作“三角形ABC”.
记三角形时,顶点字母一般按字母表中的顺序排列.
三角形的记法
图中有几个三角形?用符号表示这些三角形.
△ABC
△ABE
△BCD
△BCE
△ECD
5个
做一做
某村庄和小学分别位于两条交叉的大路边(如图).可是,每年冬天麦田弄不好就会走出一条小路来.你说小学生为什么会这样走呢?
麦
田
两点之间的所有连线中,线段最短
在A点的小狗,为了尽快吃到B点的香肠,它选择A
B路线,而不选择A
C
B路线,难道小狗也懂数学?
C
B
A
谈谈你的想法!
请拿出准备好的长度分别为:5cm,6cm,11cm,12cm的纸条各一根,从中任取三根看能不能摆成一个三角形?
从4根中取出3根有以下几种情况:
(1)5cm,6cm,11cm
通过动手发现:
(3)
(4)
可以摆成三角形,
(1)
(2)
不能摆成三角形.
(2)5cm,6cm,12cm
(3)5cm,11cm,12cm
(4)6cm,11cm,12cm
通过实验你能发现:构成一个三角形的三边有什么规律?
动手试一试
●
●
●
A
B
C
AC
+
CB
>AB
CB
+
AB
>AC
AB
+
AC
>CB
AB
-
CB
<AC
AC
-
AB
<CB
CB
-
AC
<AB
三角形任何两边之和大于第三边
三角形三边的关系
三角形任何两边的差小于第三边
1.
张老师想制作一个三角形木架,现有两根长度为19cm和9cm的木棒,第三根的长度X的取值范围是多少?
10㎝<x<28㎝
做一做
小学时我们就已经学习了三角形的相关知识,对三角形有了初步的认识.
那么,回想一下,三角形按边可以分成哪几类?按角分呢?
思考
按角的类型分
锐角三角形
直角三角形
钝角三角形
斜三角形
三角形按角分类
按边的相等关系分
不等边三角形
等腰三角形
等边三角形
底和腰不相等的等腰三角形
三角形按边分类
1.小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
小颖有5种选法.
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm
他一步能走3米,
不可能
A
B
C
答:不能.如果此人一步能走3米多,由三角形三边的关系得,此人两腿长的和得大于3米多,这与实际情况相矛盾,所以它一步不能走3米多.
你相信吗?
(姚明腿长1.28米)
3、下列长度的三条线段能否构成三角形?为什么?
2、一个三角形的两边长分别是3和8,而第三边为奇数,则第三边长为(
).
A.
5或7
B.
7
C.
9
D.
7或9
1、如果一个三角形的三边长分别为x,2,3,那么x的取值范围是
.
(2)5,6,11
(4)6,6,7
(1)3,4,8
(3)1,2,3
5>x>1
D
×
×
×
√
随堂练习
分析:在等腰三角形中,知两边长分别是4cm和9cm,故第三边长只能取4cm或9cm.若取4cm,则4+4<9,不能构成三角形;若取9cm,4+9>4,则能构成三角形,故取9cm,则它的周长为4+9+9=22cm.
5、等腰三角形的两边长分别是4cm和9cm,则它的周长为_____cm.
4、判断对错:三条线段 a、b、c,如果
a+b>c
,则一定能构成三角形.
答:错,a、b必须为较短的两条线段.
22
通过本节课的学习谈谈你的收获?
学有所得!
三角形有基本要素
边
基本要素
角
顶点
A
B
C
(AB、BC、CA)
(∠A、∠B、∠C)
(A、B、C)
如上面的三角形ABC记作:
三角形的表示:
(用符号“△”表示)
△ABC
b
c
a
三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形.
我学会了……
1、三角形的三边关系定理:
(2)确定三角形第三边的取值范围:
两边之差<第三边<两边之和
三角形的任何两边的和大于第三边
三角形的任何两边的差小于第三边
我学会了……
三角形的边
观察思考:以下的图中,都出现了什么几何图形?这种几何图形有什么特点?如何定义它?
如何定义三角形?
由3条不在同一直线上的线段,首尾顺次相接组成的图形叫做三角形.
三角形的定义
如图,线段AB、BC、AC是三角形的边.
b
c
a
边也可以用a、b、c来表示.
顶点A所对的边BC用a表示,
顶点B所对的边AC用b表示,
顶点C所对的边AB用c表示,
三角形的边
∠A、∠B、∠C是相邻两边组成的角,叫做三角形的内角,简称三角形的角.
点A、B、C是三角形的顶点.
C
A
B
三角形的顶点、角
在
ABC中,AB边所对的角是:
∠A所对的边是:
∠C
BC
★再说几个对边与对角的关系试试.
△ABC
△OPQ
记法:三角形的符号“△”,读作“三角形”;
顶点字母是A、B、C的三角形,记作“△ABC”,读作“三角形ABC”.
记三角形时,顶点字母一般按字母表中的顺序排列.
三角形的记法
图中有几个三角形?用符号表示这些三角形.
△ABC
△ABE
△BCD
△BCE
△ECD
5个
做一做
某村庄和小学分别位于两条交叉的大路边(如图).可是,每年冬天麦田弄不好就会走出一条小路来.你说小学生为什么会这样走呢?
麦
田
两点之间的所有连线中,线段最短
在A点的小狗,为了尽快吃到B点的香肠,它选择A
B路线,而不选择A
C
B路线,难道小狗也懂数学?
C
B
A
谈谈你的想法!
请拿出准备好的长度分别为:5cm,6cm,11cm,12cm的纸条各一根,从中任取三根看能不能摆成一个三角形?
从4根中取出3根有以下几种情况:
(1)5cm,6cm,11cm
通过动手发现:
(3)
(4)
可以摆成三角形,
(1)
(2)
不能摆成三角形.
(2)5cm,6cm,12cm
(3)5cm,11cm,12cm
(4)6cm,11cm,12cm
通过实验你能发现:构成一个三角形的三边有什么规律?
动手试一试
●
●
●
A
B
C
AC
+
CB
>AB
CB
+
AB
>AC
AB
+
AC
>CB
AB
-
CB
<AC
AC
-
AB
<CB
CB
-
AC
<AB
三角形任何两边之和大于第三边
三角形三边的关系
三角形任何两边的差小于第三边
1.
张老师想制作一个三角形木架,现有两根长度为19cm和9cm的木棒,第三根的长度X的取值范围是多少?
10㎝<x<28㎝
做一做
小学时我们就已经学习了三角形的相关知识,对三角形有了初步的认识.
那么,回想一下,三角形按边可以分成哪几类?按角分呢?
思考
按角的类型分
锐角三角形
直角三角形
钝角三角形
斜三角形
三角形按角分类
按边的相等关系分
不等边三角形
等腰三角形
等边三角形
底和腰不相等的等腰三角形
三角形按边分类
1.小颖要制作一个三角形木架,现有两根长度为8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
小颖有5种选法.
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm
他一步能走3米,
不可能
A
B
C
答:不能.如果此人一步能走3米多,由三角形三边的关系得,此人两腿长的和得大于3米多,这与实际情况相矛盾,所以它一步不能走3米多.
你相信吗?
(姚明腿长1.28米)
3、下列长度的三条线段能否构成三角形?为什么?
2、一个三角形的两边长分别是3和8,而第三边为奇数,则第三边长为(
).
A.
5或7
B.
7
C.
9
D.
7或9
1、如果一个三角形的三边长分别为x,2,3,那么x的取值范围是
.
(2)5,6,11
(4)6,6,7
(1)3,4,8
(3)1,2,3
5>x>1
D
×
×
×
√
随堂练习
分析:在等腰三角形中,知两边长分别是4cm和9cm,故第三边长只能取4cm或9cm.若取4cm,则4+4<9,不能构成三角形;若取9cm,4+9>4,则能构成三角形,故取9cm,则它的周长为4+9+9=22cm.
5、等腰三角形的两边长分别是4cm和9cm,则它的周长为_____cm.
4、判断对错:三条线段 a、b、c,如果
a+b>c
,则一定能构成三角形.
答:错,a、b必须为较短的两条线段.
22
通过本节课的学习谈谈你的收获?
学有所得!
三角形有基本要素
边
基本要素
角
顶点
A
B
C
(AB、BC、CA)
(∠A、∠B、∠C)
(A、B、C)
如上面的三角形ABC记作:
三角形的表示:
(用符号“△”表示)
△ABC
b
c
a
三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形.
我学会了……
1、三角形的三边关系定理:
(2)确定三角形第三边的取值范围:
两边之差<第三边<两边之和
三角形的任何两边的和大于第三边
三角形的任何两边的差小于第三边
我学会了……
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
