沪科版九年级下册数学 24.7 弧长与扇形面积课件(共15张PPT)
文档属性
| 名称 | 沪科版九年级下册数学 24.7 弧长与扇形面积课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 12:55:47 | ||
图片预览




文档简介
(共15张PPT)
24.7弧长和扇形面积(1)
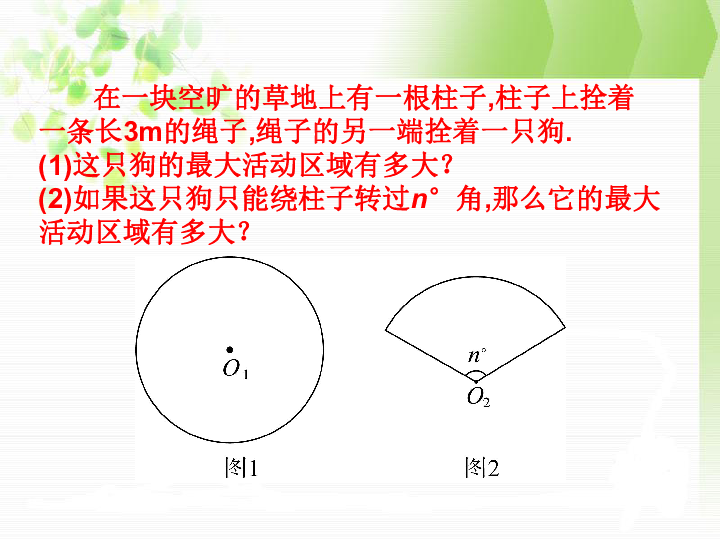
在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?
例1
一滑轮装置如图24-63,滑轮的半径R=10cm,当重物上升15.7cm时,问滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度?(假设绳索与滑轮之间没有滑动,π取3.14)
答:滑轮按逆时针方向旋转的角度约为90°.
解
设半径OA绕轴心O按逆时针方向旋转n°,则
解方程,得
n≈90.
例2
古希腊埃拉托塞尼曾给出一个估算地球周长
(或子午圈长)的简单方法.如图24-64,点S和点A分别表示埃及的赛伊尼和亚历山大两地,亚历山大在赛伊尼的北方,两地的经度大致相同,两地的实际距离为5000希腊里(1希腊里≈158.5m).当太阳光线在赛伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射方向的角为α,实际测得α是7.2°,由此估算出了地球的周长,你能进行计算吗?
解
因为太阳光线可看作平行的,所以圆心角∠AOS=α=7.2°.
设地球的周长(即⊙O的周长)为C,则
(希腊里)
答:地球的周长约为39625km.
我们知道,地球周长约为40000m.可见,2000前,埃拉托塞尼的估算结果已经相当精确了.
≈39625(km)
圆柱与圆锥的侧面积
探究新知
探究新知
圆锥的底面半径、高线、母线长三者之间的关系:
例如:已知一个圆锥的高为6cm,半径为8cm,则这个圆锥的母长为_______
10cm
h
r
O
2.圆锥的母线l
1.圆锥的高h
点击概念
圆锥是由一个底面和一个侧面围成的,它的底面是一个圆,侧面是一个曲面.
(思考:圆锥的母线有几条?)
3.底面半径r
h
r
O
准备好的圆锥模型沿着母线剪开,观察圆锥的侧面展开图.
探究新知
h
r
O
圆柱与圆锥的侧面积
归纳总结
思考:
探究新知
你能探究展开图中的圆心角n与
r
、
之间的关系吗?
)
n
h
r
O
例3如图24-66,圆锥形的烟囱帽,它的底面直径为80cm,母线为50cm.在一块大铁皮上剪裁时,如何画出这个烟囱帽的侧面展开图?求出该侧面展开图的面积.
解
烟囱帽的侧面展开图是扇形,如图24-67,设该扇形的面积为S.
在铁皮上画一个扇形,除需知道扇形半径l外,还需知道扇形圆心角α.由刚学过的弧长计算方法,可得
随堂练习
圆锥的侧面积为
,其轴截面是一个等边三角形,则该轴截面的面积(
)
B
.
C.
D.
A
r
h
小结:
1.圆锥的侧面积和全面积
2.
展开图中的圆心角n与r、R之间的关系:
24.7弧长和扇形面积(1)
在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?
例1
一滑轮装置如图24-63,滑轮的半径R=10cm,当重物上升15.7cm时,问滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度?(假设绳索与滑轮之间没有滑动,π取3.14)
答:滑轮按逆时针方向旋转的角度约为90°.
解
设半径OA绕轴心O按逆时针方向旋转n°,则
解方程,得
n≈90.
例2
古希腊埃拉托塞尼曾给出一个估算地球周长
(或子午圈长)的简单方法.如图24-64,点S和点A分别表示埃及的赛伊尼和亚历山大两地,亚历山大在赛伊尼的北方,两地的经度大致相同,两地的实际距离为5000希腊里(1希腊里≈158.5m).当太阳光线在赛伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射方向的角为α,实际测得α是7.2°,由此估算出了地球的周长,你能进行计算吗?
解
因为太阳光线可看作平行的,所以圆心角∠AOS=α=7.2°.
设地球的周长(即⊙O的周长)为C,则
(希腊里)
答:地球的周长约为39625km.
我们知道,地球周长约为40000m.可见,2000前,埃拉托塞尼的估算结果已经相当精确了.
≈39625(km)
圆柱与圆锥的侧面积
探究新知
探究新知
圆锥的底面半径、高线、母线长三者之间的关系:
例如:已知一个圆锥的高为6cm,半径为8cm,则这个圆锥的母长为_______
10cm
h
r
O
2.圆锥的母线l
1.圆锥的高h
点击概念
圆锥是由一个底面和一个侧面围成的,它的底面是一个圆,侧面是一个曲面.
(思考:圆锥的母线有几条?)
3.底面半径r
h
r
O
准备好的圆锥模型沿着母线剪开,观察圆锥的侧面展开图.
探究新知
h
r
O
圆柱与圆锥的侧面积
归纳总结
思考:
探究新知
你能探究展开图中的圆心角n与
r
、
之间的关系吗?
)
n
h
r
O
例3如图24-66,圆锥形的烟囱帽,它的底面直径为80cm,母线为50cm.在一块大铁皮上剪裁时,如何画出这个烟囱帽的侧面展开图?求出该侧面展开图的面积.
解
烟囱帽的侧面展开图是扇形,如图24-67,设该扇形的面积为S.
在铁皮上画一个扇形,除需知道扇形半径l外,还需知道扇形圆心角α.由刚学过的弧长计算方法,可得
随堂练习
圆锥的侧面积为
,其轴截面是一个等边三角形,则该轴截面的面积(
)
B
.
C.
D.
A
r
h
小结:
1.圆锥的侧面积和全面积
2.
展开图中的圆心角n与r、R之间的关系:
