9.4解直角三角形（4）

(共11张PPT)
温故知新
1.
2.
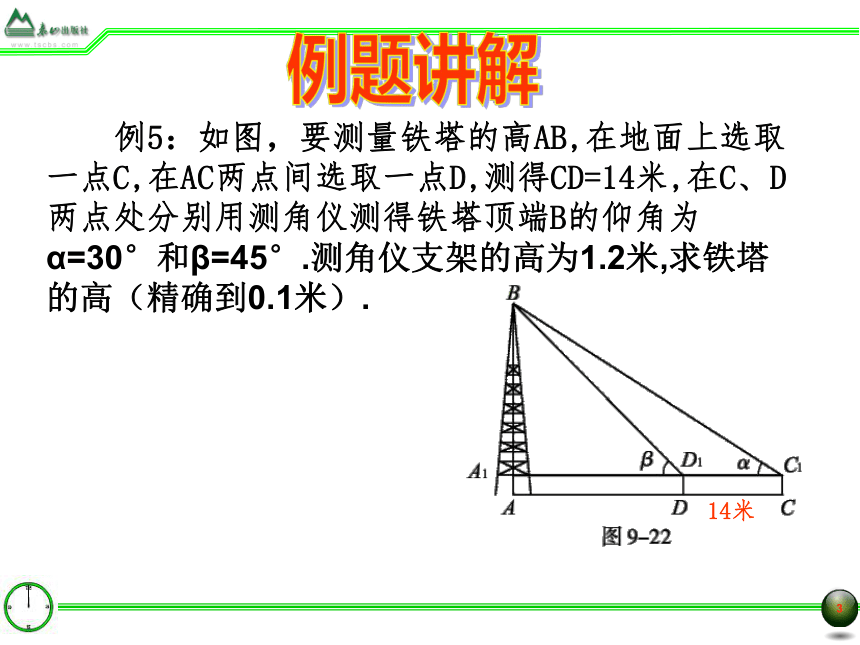
例5：如图，要测量铁塔的高AB,在地面上选取一点C,在AC两点间选取一点D,测得CD=14米,在C、D两点处分别用测角仪测得铁塔顶端B的仰角为α=30°和β=45°.测角仪支架的高为1.2米,求铁塔的高（精确到0.1米）.
14米
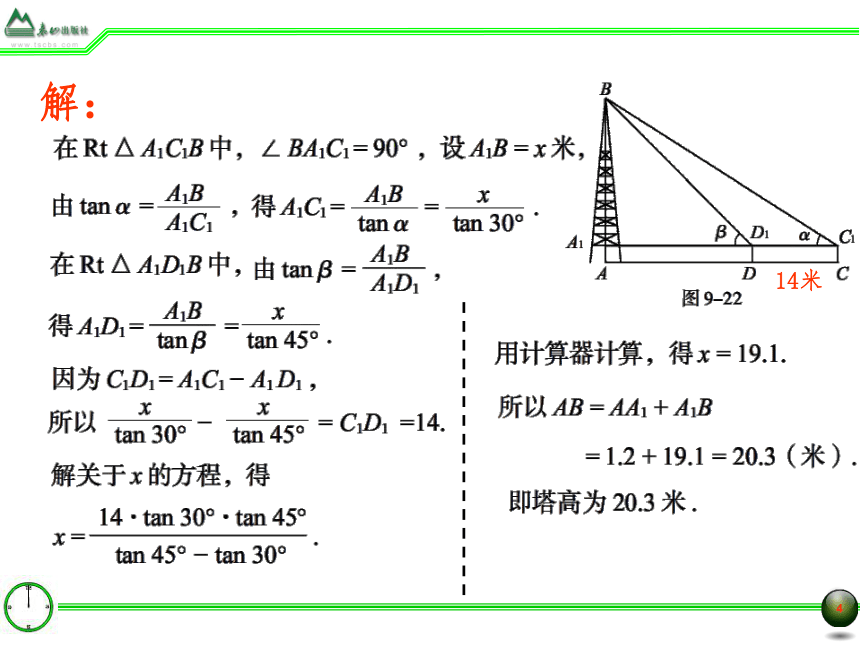
解：
14米
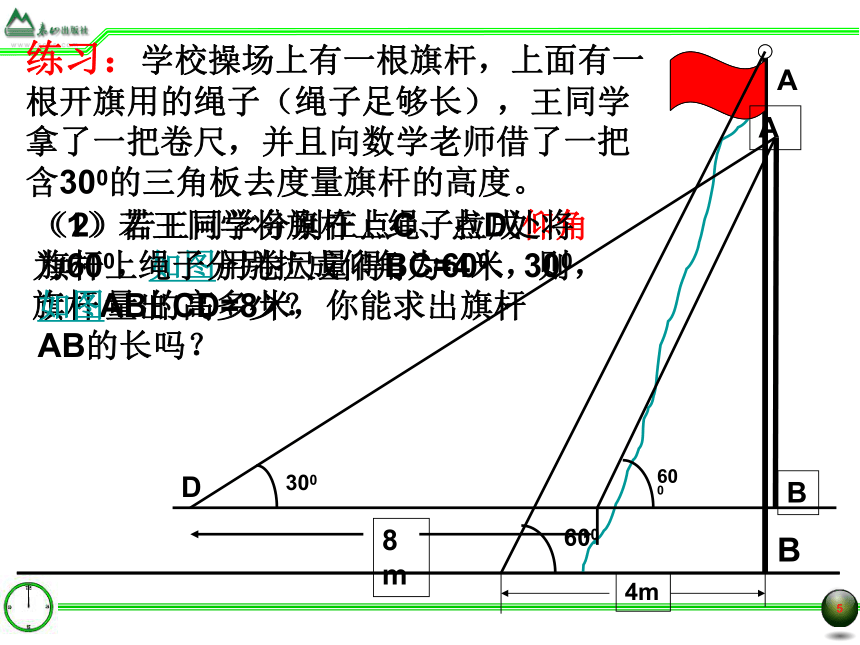
练习：学校操场上有一根旗杆，上面有一根开旗用的绳子（绳子足够长），王同学拿了一把卷尺，并且向数学老师借了一把含300的三角板去度量旗杆的高度。
（1）若王同学将旗杆上绳子拉成仰角为600，如图用卷尺量得BC=4米，则旗杆AB的高多少？
（2）若王同学分别在点C、点D处将旗杆上绳子分别拉成仰角为600、300，如图量出CD=8米，你能求出旗杆AB的长吗？
A
B
4m
600
A
B
D
8m
300
600
船有无触礁的危险？
如图,海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西550的B处,往东行驶20海里后到达该岛的南偏西250的C处.之后,货轮继续向东航行.
要解决这个问题,我们可以将其数学化,如图:
你认为货轮继续向东航行途中会有触礁的危险吗
A
B
C
D
北
东
要知道货轮继续向东航行途中有无触礁的危险,只要过点A作AD⊥BC的延长线于点D,如果AD>10海里,则无触礁的危险
┌
A
B
C
D
北
东
550
250
解:过点A作AD⊥BC的延长线于点D,如果AD>10海里,则无触礁的危险.
答:货轮继续向东航行途中没有触礁的危险.
┌
A
B
C
D
北
东
550
250
根据题意可知,∠BAD=550,∠CAD=250,BC= 20海里.设AD=x,则
20.0海里
在两个或多个直角三角形中，根据它们之间的边角关系,利用解直角三角形的知识解决实际问题.
抽象出实际问题中的直角三角形，或通过作辅助线构造直 角三角形.
1.
2.