沪科版七年级下数学:10.1.2相交线(2)垂线课件(共15张PPT)
文档属性
| 名称 | 沪科版七年级下数学:10.1.2相交线(2)垂线课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
请思考生活中相交线的特殊性
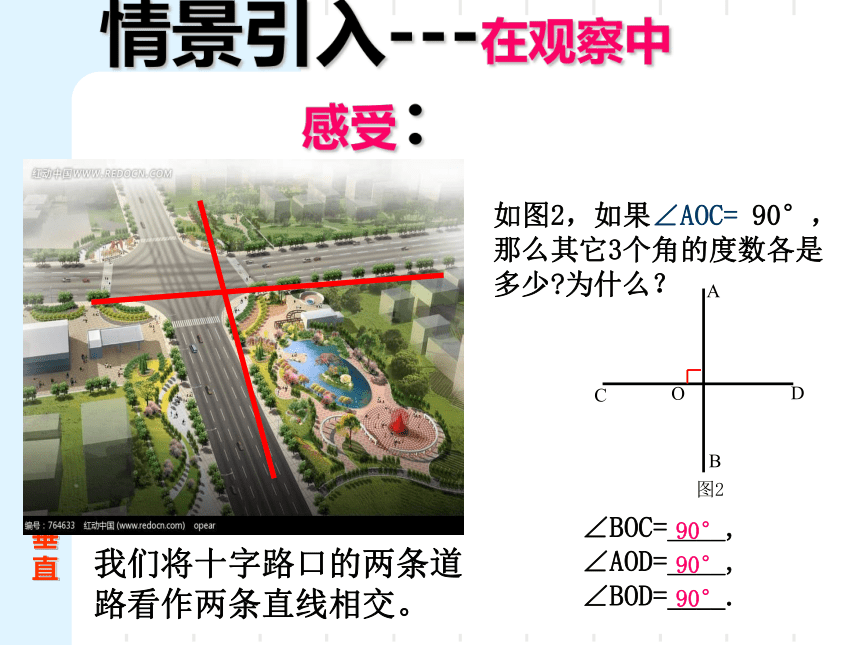
情景引入---在观察中感受:
我们将十字路口的两条道路看作两条直线相交。
如图2,如果∠AOC=
90°,那么其它3个角的度数各是多少?为什么?
∠BOC=____,
∠AOD=____,
∠BOD=____.
90°
90°
90°
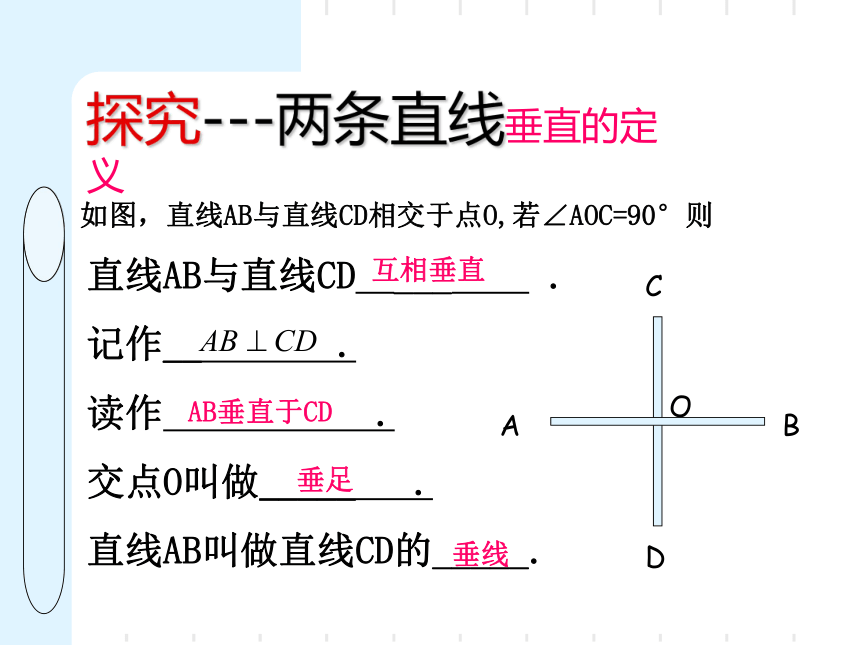
探究---两条直线垂直的定义
O
如图,直线AB与直线CD相交于点O,若∠AOC=90°则
直线AB与直线CD
___
.
记作__
.
读作
.
交点O叫做_____
.
直线AB叫做直线CD的_____.
互相垂直
垂足
垂线
AB垂直于CD
记作:_________,
垂足为___.
记作:
,垂足为____.
练一练
MN⊥EF
O
AB⊥CE
C
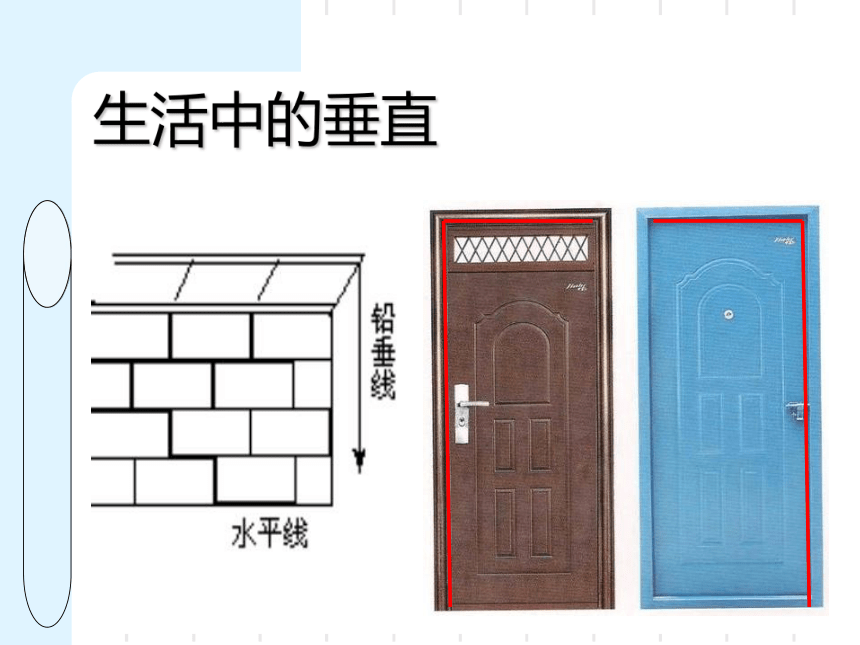
生活中的垂直
活动探究---在实践中收获:
【操作】
1、过直线L上一点画已知直线的垂线
2、过直线L外一点画已知直线的垂线
【思考】如何过一点画已知直线的垂线?
3、你能通过折纸的方法画垂线吗?
活动探究---在实践中收获:
问题:
这样过一点画L的垂线可以画几条?
1
条
注意:在连接直线外一点与直线上个点的所
连线中垂线段最短
垂线段:连接直线外一点与垂足形成的线段。
根据以上的操作,你能得出什么结论?
过一点有且只有一条直线垂直于已知直线。
归纳总结---垂线的基本事实
练一练---在应用中提升:
垂直(
OE⊥AB
)
1、如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35°
∠2=55°,请判断直线OE与AB的位置关系。为什么?
练一练---在应用中提升:
2、如图
,已知AB.
CD相交于O,
OE⊥CD
于O,∠AOC=36°,则∠BOE=
。
(A)36°
(B)
64°
(C)144°
(D)
54°
54°
3、过点P
向线段AB
所在直线引垂线,正确的是(
)
A
B
C
D
C
练一练---在应用中提升:
P
O
A
B
点到射线或线段的垂线指的是点到射线或线段所在直线的垂线
练一练---在应用中提升:
4、如图,过点P画出∠AOB两边的垂线。
交流体会---在反思中发展:
【畅谈你的心得、体会】
【谈谈你遇到的困难】
作业训练
1、课本P120练习1
P121习题2、3
2、基础训练同步
拓展---在应用中提升:
【拓展思考】如图,OA
⊥OB,
∠AOC=
∠BOD,
试分析OC与OD的位置关系?你能说明你的结论
吗?
请思考生活中相交线的特殊性
情景引入---在观察中感受:
我们将十字路口的两条道路看作两条直线相交。
如图2,如果∠AOC=
90°,那么其它3个角的度数各是多少?为什么?
∠BOC=____,
∠AOD=____,
∠BOD=____.
90°
90°
90°
探究---两条直线垂直的定义
O
如图,直线AB与直线CD相交于点O,若∠AOC=90°则
直线AB与直线CD
___
.
记作__
.
读作
.
交点O叫做_____
.
直线AB叫做直线CD的_____.
互相垂直
垂足
垂线
AB垂直于CD
记作:_________,
垂足为___.
记作:
,垂足为____.
练一练
MN⊥EF
O
AB⊥CE
C
生活中的垂直
活动探究---在实践中收获:
【操作】
1、过直线L上一点画已知直线的垂线
2、过直线L外一点画已知直线的垂线
【思考】如何过一点画已知直线的垂线?
3、你能通过折纸的方法画垂线吗?
活动探究---在实践中收获:
问题:
这样过一点画L的垂线可以画几条?
1
条
注意:在连接直线外一点与直线上个点的所
连线中垂线段最短
垂线段:连接直线外一点与垂足形成的线段。
根据以上的操作,你能得出什么结论?
过一点有且只有一条直线垂直于已知直线。
归纳总结---垂线的基本事实
练一练---在应用中提升:
垂直(
OE⊥AB
)
1、如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35°
∠2=55°,请判断直线OE与AB的位置关系。为什么?
练一练---在应用中提升:
2、如图
,已知AB.
CD相交于O,
OE⊥CD
于O,∠AOC=36°,则∠BOE=
。
(A)36°
(B)
64°
(C)144°
(D)
54°
54°
3、过点P
向线段AB
所在直线引垂线,正确的是(
)
A
B
C
D
C
练一练---在应用中提升:
P
O
A
B
点到射线或线段的垂线指的是点到射线或线段所在直线的垂线
练一练---在应用中提升:
4、如图,过点P画出∠AOB两边的垂线。
交流体会---在反思中发展:
【畅谈你的心得、体会】
【谈谈你遇到的困难】
作业训练
1、课本P120练习1
P121习题2、3
2、基础训练同步
拓展---在应用中提升:
【拓展思考】如图,OA
⊥OB,
∠AOC=
∠BOD,
试分析OC与OD的位置关系?你能说明你的结论
吗?
