北京课改版八年级下册数学16.2一元二次方程解法——开平方法课件(98张ppt)
文档属性
| 名称 | 北京课改版八年级下册数学16.2一元二次方程解法——开平方法课件(98张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 00:00:00 | ||
图片预览










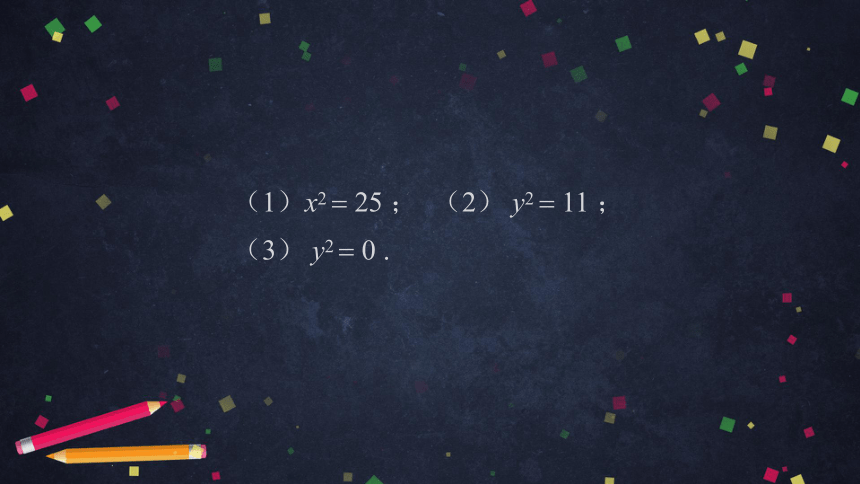

文档简介
(共98张PPT)
初二年级
数学
一元二次方程解法——开平方法
ax2+bx+c
=0(a>0)
c>0
c<0
b>0
b
=
0
b<0
x2+5x
=
0.
2x2-3
=
0;
k2-16
=
0.
y2+3y+1=
0.
7y2+5
=
0.
x2-2x+6
=
0.
2x2-2x
=
0;
3m2-4m
=
0.
3m2-3m-5
=
0;
x2-3x-10
=
0;
3x2-8x-10
=
0.
2.4m2+6m-5
=
0;
4m2+6m-5
=
0;
2a2+10a-10
=
0.
9a2
=
0;
x2
=
0.
c
=
0
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根.
平方根
也就是说,如果x2
=
a,那么x叫做a的平方根,记作x
=±
(
a≥0
)
.
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根.
平方根
也就是说,如果x2
=
a,那么x叫做a的平方根,记作x
=±
(
a≥0
)
.
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根.
平方根
求一个数a的平方根的运算叫做开平方.
你能根据平方根的意义求出下列一元二次方程的解吗?
(1)x2
=
25
;
(2)
y2
=
11
;
(3)
y2
=
0
;
(4)
x2
=
-2.
问题
解:
(1)开平方,得
x
=±5.
所以,这个方程的解是
x1=
5
或
x2
=
-5.
(1)x2
=
25.
y
=±
.
解:
(2)
开平方,得
所以,这个方程的解是
y1=
或
y2=-
.
(2)
y2
=
11.
解
:
(3)开平方,得
所以,这个方程的解是
y1
=
y2
=
0.
(3)
y2
=
0.
解:
(4)
x2=
-2;
因为对任意实数x,都有x2≥0;
所以,方程x2
=
-2无实数解.
(1)x2
=
25
;
(2)
y2
=
11
;
(3)
y2
=
0
.
形如x2
=
m(m≥0)的方程可以用开平方求出方程的解,这种解法称为开平方法.
一般形式:
.
开平方法
方程
方程解的情况
方程的解
方程
方程解的情况
方程的解
x2
=
25
x1=5
或
x2=-5
方程
方程解的情况
方程的解
x2
=
25
x1=5
或
x2=-5
两个不相等的实数解,
且两个解互为相反数.
方程
方程解的情况
方程的解
x2
=
25
y2
=
11
x1=5
或
x2=-5
y1=
或
y2=-
两个不相等的实数解,
且两个解互为相反数.
方程
方程解的情况
方程的解
两个不相等的实数解,
且两个解互为相反数.
x2
=
25
y2
=
11
x1=5
或
x2=-5
y1=
或
y2=-
两个不相等的实数解,
且两个解互为相反数.
方程
方程解的情况
方程的解
两个不相等的实数解,
且两个解互为相反数.
x2
=
25
y2
=
11
y2
=
0
x1=5
或
x2=-5
y1=
或
y2=-
y1
=
y2
=
0
两个不相等的实数解,
且两个解互为相反数.
方程
方程解的情况
方程的解
两个不相等的实数解,
且两个解互为相反数.
x2
=
25
y2
=
11
y2
=
0
x1=5
或
x2=-5
y1=
或
y2=-
y1
=
y2
=
0
两个相等的实数解,
且两个解都是零.
两个不相等的实数解,
且两个解互为相反数.
方程
方程解的情况
方程的解
两个不相等的实数解,
且两个解互为相反数.
x2
=
25
y2
=
11
y2
=
0
x2
=
-2
x1=5
或
x2=-5
y1=
或
y2=-
y1
=
y2
=
0
两个相等的实数解,
且两个解都是零.
两个不相等的实数解,
且两个解互为相反数.
无解
方程
方程解的情况
方程的解
两个不相等的实数解,
且两个解互为相反数.
x2
=
25
y2
=
11
y2
=
0
x2
=
-2
x1=5
或
x2=-5
y1=
或
y2=-
y1
=
y2
=
0
两个相等的实数解,
且两个解都是零.
两个不相等的实数解,
且两个解互为相反数.
没有实数解.
无解
m的取值
方程解的情况
方程解的表示
?
?
思考:
方程x2
=
m的解有哪些情况.
m的取值
方程解的情况
方程解的表示
?
?
思考:
方程x2
=
m的解有哪些情况.
m>0
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
?
思考:
方程x2
=
m的解有哪些情况.
m>0
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
?
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
两个相等的实数解,
且两个解都是零.
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
?
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
两个相等的实数解,
且两个解都是零.
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
x1=
x2=0?
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
两个相等的实数解,
且两个解都是零.
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
m<0
x1=
x2=0?
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
两个相等的实数解,
且两个解都是零.
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
m<0
x1=
x2=0?
没有实数解.
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
两个相等的实数解,
且两个解都是零.
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
m<0
x1=
x2=0?
没有实数解.
无解
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
两个相等的实数解,
且两个解都是零.
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
m<0
x1=
x2=0?
没有实数解.
无解
注:一元二次方程,有可能有解,也可能无解,有解必有两个.
例1.用开平方法解下列方程.
(1)x2
=121;
(2)9y2
=
25
;
(3)3a2-81=
0.
(1)x2
=121.
(1)x2
=121.
解:
(1)开平方,得
(1)x2
=121.
所以,这个方程的解是
x1=11
或
x2=
-11.
(2)9y2
=
25.
.
解:(2)方程两边同除以9,得
(2)9y2
=
25.
.
解:(2)方程两边同除以9,得
开平方,得
.
所以,这个方程的解是
.
(2)9y2
=
25.
(3)3a2-81=
0.
解:(3)
移项,得
系数化1,得
3a2
=
81.
a2
=
27.
(3)3a2-81=
0.
解:(3)
移项,得
系数化1,得
3a2
=
81.
a2
=
27.
开平方,得
.
所以,这个方程的解是
.
化成最简二次根式
(3)3a2-81=
0.
解题步骤
解题步骤
(1)将方程整理成x2
=
m的形式.
解题步骤
(1)将方程整理成x2
=
m的形式.
(2)若m≥0利用开平方法求出方程的解;
若m<0
,此方程无实数解.
解题步骤
(1)将方程整理成x2
=
m的形式.
(2)若m≥0利用开平方法求出方程的解;
若m<0
,此方程无实数解.
注:开平方后的结果要化简.
例2.用开平方法解下列方程.
(1)(x-3)2
=16
;
(2)4(t+4)2
=
9
;
(3)2(n
-2-1=
0.
(1)(x-3)2
=16.
(1)(x-3)2
=16.
将x-3看成一个整体
解:
(1)开平方,得
x-3
=±
.
x-3
=±4.
(1)(x-3)2
=16.
解:
(1)开平方,得
x-3
=±
.
x-3
=±4.
x-3
=
4
或
x-3
=
-
4.
(1)(x-3)2
=16.
解:
(1)开平方,得
x-3
=±
.
x-3
=±4.
x-3
=
4
或
x-3
=
-
4.
(1)(x-3)2
=16.
解:
(1)开平方,得
x-3
=±
.
x-3
=±4.
x-3
=
4
或
x-3
=
-
4.
所以,这个方程的解是
x1=7
,
x2=
-1.
(1)(x-3)2
=16.
(x-3)2
=16.
(ax
+
c)2
=
m
(a≠0,m≥0)
开平方
求解
开平方
求解
(2)4(t+4)2=9.
(ax
+
c)2
=
m
(a≠0,m≥0)
(t+4)2=
.
(2)4(t+4)2=9.
解:(2)方程整理,得
开平方,得
所以这个方程的解是
,
.
.
(3)
2(n
-
2-1=0.
(ax
+
c)2
=
m
(a≠0,m≥0)
解:(3)
移项
,得
2(n
-
2=1.
(3)
2(n
-
2-1=0.
解:(3)
移项
,得
2(n
-
2=1.
(3)
2(n
-
2-1=0.
整理,得
(n
-
)2=
.
解:(3)
移项
,得
2(n
-
2=1.
(3)
2(n
-
2-1=0.
整理,得
(n
-
)2=
.
开平方,得
n
-
=±
.
n
-
=±
.
由
,得
.
由
,得
.
所以这个方程的解是
n1=
,
n2=
.
解题步骤
(1)将方程整理成(ax
+
c)2
=
m
(a≠0,m≥0)的形式.
(2)利用开平方法得到两个一元一次方程
(降次).
(3)分别求这两个一元一次方程的解.
(4)这两个一元一次方程的解就是原方程的解.
一元二次方程
一元二次方程
一元二次方程
开平方
降次
一元二次方程
开平方
降次
一元一次方程
一元二次方程
开平方
降次
一元一次方程
一元二次方程
开平方
降次
一元一次方程
求解
一元二次方程
开平方
降次
一元一次方程
求解
x1,
x2
一元二次方程
开平方
降次
一元一次方程
求解
x1,
x2
练习
1.用开平方法解下列方程.
(3)
(3x+1)2
=
7
;
(4)
x2-4x+4
=
9
.
(1)
4x2=81;
(2)
(2x-3)2-25=-9;
(1)
4x2
=81.
解:(1)方程两边同时除以4,得
.
开平方,得
.
所以方程的解是
.
(1)
4x2
=81.
4x2
=
81
解:(2)移项,得
(2x-3)2=-9+25
=16
.
开平方,得
2x-3=±4
.
2x-3=4
或
2x-3=-4
.
所以方程的解是
.
(2)
(2x-3)2-25=-9.
(3)
(3x+1)2
=
7.
开平方,得
.
(3)
(3x+1)2
=
7.
解:(3)两边都乘以
,
(3x+1)2
=
5.
由
,得
.
由
,得
x
=
.
所以这个方程的解是
x1=
,x2=
.
(4)
x2-4x+4=
9.
(4)
x2-4x+4=
9.
解:方程整理,得
(x-2)2=
9.
利用完全平方公式将等号左边进行变形
(4)
x2-4x+4=
9.
解:方程整理,得
(x-2)2=
9.
利用完全平方公式将等号左边进行变形
开平方,得
x-2=±3.
x-2=3
或
x-2=-3.
(4)
x2-4x+4=
9.
解:方程整理,得
(x-2)2=
9.
利用完全平方公式将等号左边进行变形
开平方,得
x-2=±3.
所以这个方程的解是
x1=
5,x2=
-1.
x-2=3
或
x-2=-3.
2.若一元二次方程ax2=
b(a
b>0)的两个解分别是m+1与2m-4,则
=__
.
2.若一元二次方程ax2=
b(a
b>0)的两个解分别是m+1与2m-4,则
=__
.
分析:由ax2=b变形为x2=
,因为a
b>0,所以
>0
,
2.若一元二次方程ax2=
b(a
b>0)的两个解分别是m+1与2m-4,则
=__
.
分析:由ax2=b变形为x2=
,因为a
b>0,所以
>0
,所以方程
x2=
的两个解互为相反数,
2.若一元二次方程ax2=
b(a
b>0)的两个解分别是m+1与2m-4,则
=__
.
分析:由ax2=b变形为x2=
,因为a
b>0,所以
>0
,所以方程
x2=
的两个解互为相反数,
所以m+1+2m-4=0,解得m=1,
2.若一元二次方程ax2=
b(a
b>0)的两个解分别是m+1与2m-4,则
=__
.
分析:由ax2=b变形为x2=
,因为a
b>0,所以
>0
,所以方程
x2=
的两个解互为相反数,
所以m+1+2m-4=0,解得m=1,所以x1=m+1=2,x2=-2,
2.若一元二次方程ax2=
b(a
b>0)的两个解分别是m+1与2m-4,则
=_4_
.
分析:由ax2=b变形为x2=
,因为a
b>0,所以
>0
,所以方程
x2=
的两个解互为相反数,
所以m+1+2m-4=0,解得m=1,所以x1=m+1=2,x2=-2,所以
=4
.
小结
小结
1.形如x2
=
m(m≥0)的方程可以用开平方求出
方程的解,这种解法称为开平方法.
小结
1.形如x2
=
m(m≥0)的方程可以用开平方求出
方程的解,这种解法称为开平方法.
2.方程x2
=
m的解的情况.
?
?
m>0
m
=
0
m<0
方程解的情况
方程解的表示
x1=
x2=0
无解
没有实数解.
两个不相等的实数解,两个解互为相反数.
有两个相等的实数解,两个解都是0.
一元二次方程,有可能有解,也可能无解,有解必有两个.
3.利用开平方法解一元二次方程的一般步骤.
3.利用开平方法解一元二次方程的一般步骤.
(1)将方程整理成x2
=
m或(ax
+
c)2
=
m
(a≠0,m≥0)的形式;
3.利用开平方法解一元二次方程的一般步骤.
(1)将方程整理成x2
=
m或(ax
+
c)2
=
m
(a≠0,m≥0)的形式;
(2)利用开平方法得到两个一元一次方程(降次);
3.利用开平方法解一元二次方程的一般步骤.
(1)将方程整理成x2
=
m或(ax
+
c)2
=
m
(a≠0,m≥0)的形式;
(2)利用开平方法得到两个一元一次方程(降次);
(3)求这两个一元一次方程的解;
3.利用开平方法解一元二次方程的一般步骤.
(1)将方程整理成x2
=
m或(ax
+
c)2
=
m
(a≠0,m≥0)的形式;
(2)利用开平方法得到两个一元一次方程(降次);
(3)求这两个一元一次方程的解;
(4)这两个一元一次方程的解就是原方程的解;
3.利用开平方法解一元二次方程的一般步骤.
(1)将方程整理成x2
=
m或(ax
+
c)2
=
m
(a≠0,m≥0)的形式;
(2)利用开平方法得到两个一元一次方程(降次);
(3)求这两个一元一次方程的解;
(4)这两个一元一次方程的解就是原方程的解;
(5)结果要化简.
A组:1.用开平方法解下列方程.
(1)
x2-289
=
0;
(2)
3x2-75=
0.
B组:2.用开平方法解下列方程.
(1)3(a-1)2-2
=
0;
(2)121-25(y+
2=
0.
作业
祝同学们学习愉快!
初二年级
数学
一元二次方程解法——开平方法
ax2+bx+c
=0(a>0)
c>0
c<0
b>0
b
=
0
b<0
x2+5x
=
0.
2x2-3
=
0;
k2-16
=
0.
y2+3y+1=
0.
7y2+5
=
0.
x2-2x+6
=
0.
2x2-2x
=
0;
3m2-4m
=
0.
3m2-3m-5
=
0;
x2-3x-10
=
0;
3x2-8x-10
=
0.
2.4m2+6m-5
=
0;
4m2+6m-5
=
0;
2a2+10a-10
=
0.
9a2
=
0;
x2
=
0.
c
=
0
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根.
平方根
也就是说,如果x2
=
a,那么x叫做a的平方根,记作x
=±
(
a≥0
)
.
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根.
平方根
也就是说,如果x2
=
a,那么x叫做a的平方根,记作x
=±
(
a≥0
)
.
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根.
平方根
求一个数a的平方根的运算叫做开平方.
你能根据平方根的意义求出下列一元二次方程的解吗?
(1)x2
=
25
;
(2)
y2
=
11
;
(3)
y2
=
0
;
(4)
x2
=
-2.
问题
解:
(1)开平方,得
x
=±5.
所以,这个方程的解是
x1=
5
或
x2
=
-5.
(1)x2
=
25.
y
=±
.
解:
(2)
开平方,得
所以,这个方程的解是
y1=
或
y2=-
.
(2)
y2
=
11.
解
:
(3)开平方,得
所以,这个方程的解是
y1
=
y2
=
0.
(3)
y2
=
0.
解:
(4)
x2=
-2;
因为对任意实数x,都有x2≥0;
所以,方程x2
=
-2无实数解.
(1)x2
=
25
;
(2)
y2
=
11
;
(3)
y2
=
0
.
形如x2
=
m(m≥0)的方程可以用开平方求出方程的解,这种解法称为开平方法.
一般形式:
.
开平方法
方程
方程解的情况
方程的解
方程
方程解的情况
方程的解
x2
=
25
x1=5
或
x2=-5
方程
方程解的情况
方程的解
x2
=
25
x1=5
或
x2=-5
两个不相等的实数解,
且两个解互为相反数.
方程
方程解的情况
方程的解
x2
=
25
y2
=
11
x1=5
或
x2=-5
y1=
或
y2=-
两个不相等的实数解,
且两个解互为相反数.
方程
方程解的情况
方程的解
两个不相等的实数解,
且两个解互为相反数.
x2
=
25
y2
=
11
x1=5
或
x2=-5
y1=
或
y2=-
两个不相等的实数解,
且两个解互为相反数.
方程
方程解的情况
方程的解
两个不相等的实数解,
且两个解互为相反数.
x2
=
25
y2
=
11
y2
=
0
x1=5
或
x2=-5
y1=
或
y2=-
y1
=
y2
=
0
两个不相等的实数解,
且两个解互为相反数.
方程
方程解的情况
方程的解
两个不相等的实数解,
且两个解互为相反数.
x2
=
25
y2
=
11
y2
=
0
x1=5
或
x2=-5
y1=
或
y2=-
y1
=
y2
=
0
两个相等的实数解,
且两个解都是零.
两个不相等的实数解,
且两个解互为相反数.
方程
方程解的情况
方程的解
两个不相等的实数解,
且两个解互为相反数.
x2
=
25
y2
=
11
y2
=
0
x2
=
-2
x1=5
或
x2=-5
y1=
或
y2=-
y1
=
y2
=
0
两个相等的实数解,
且两个解都是零.
两个不相等的实数解,
且两个解互为相反数.
无解
方程
方程解的情况
方程的解
两个不相等的实数解,
且两个解互为相反数.
x2
=
25
y2
=
11
y2
=
0
x2
=
-2
x1=5
或
x2=-5
y1=
或
y2=-
y1
=
y2
=
0
两个相等的实数解,
且两个解都是零.
两个不相等的实数解,
且两个解互为相反数.
没有实数解.
无解
m的取值
方程解的情况
方程解的表示
?
?
思考:
方程x2
=
m的解有哪些情况.
m的取值
方程解的情况
方程解的表示
?
?
思考:
方程x2
=
m的解有哪些情况.
m>0
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
?
思考:
方程x2
=
m的解有哪些情况.
m>0
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
?
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
两个相等的实数解,
且两个解都是零.
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
?
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
两个相等的实数解,
且两个解都是零.
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
x1=
x2=0?
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
两个相等的实数解,
且两个解都是零.
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
m<0
x1=
x2=0?
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
两个相等的实数解,
且两个解都是零.
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
m<0
x1=
x2=0?
没有实数解.
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
两个相等的实数解,
且两个解都是零.
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
m<0
x1=
x2=0?
没有实数解.
无解
m的取值
方程解的情况
方程解的表示
两个不相等的实数解,
且两个解互为相反数.
?
两个相等的实数解,
且两个解都是零.
?
x1
=
或
x2
=-
思考:
方程x2
=
m的解有哪些情况.
m>0
m
=
0
m<0
x1=
x2=0?
没有实数解.
无解
注:一元二次方程,有可能有解,也可能无解,有解必有两个.
例1.用开平方法解下列方程.
(1)x2
=121;
(2)9y2
=
25
;
(3)3a2-81=
0.
(1)x2
=121.
(1)x2
=121.
解:
(1)开平方,得
(1)x2
=121.
所以,这个方程的解是
x1=11
或
x2=
-11.
(2)9y2
=
25.
.
解:(2)方程两边同除以9,得
(2)9y2
=
25.
.
解:(2)方程两边同除以9,得
开平方,得
.
所以,这个方程的解是
.
(2)9y2
=
25.
(3)3a2-81=
0.
解:(3)
移项,得
系数化1,得
3a2
=
81.
a2
=
27.
(3)3a2-81=
0.
解:(3)
移项,得
系数化1,得
3a2
=
81.
a2
=
27.
开平方,得
.
所以,这个方程的解是
.
化成最简二次根式
(3)3a2-81=
0.
解题步骤
解题步骤
(1)将方程整理成x2
=
m的形式.
解题步骤
(1)将方程整理成x2
=
m的形式.
(2)若m≥0利用开平方法求出方程的解;
若m<0
,此方程无实数解.
解题步骤
(1)将方程整理成x2
=
m的形式.
(2)若m≥0利用开平方法求出方程的解;
若m<0
,此方程无实数解.
注:开平方后的结果要化简.
例2.用开平方法解下列方程.
(1)(x-3)2
=16
;
(2)4(t+4)2
=
9
;
(3)2(n
-2-1=
0.
(1)(x-3)2
=16.
(1)(x-3)2
=16.
将x-3看成一个整体
解:
(1)开平方,得
x-3
=±
.
x-3
=±4.
(1)(x-3)2
=16.
解:
(1)开平方,得
x-3
=±
.
x-3
=±4.
x-3
=
4
或
x-3
=
-
4.
(1)(x-3)2
=16.
解:
(1)开平方,得
x-3
=±
.
x-3
=±4.
x-3
=
4
或
x-3
=
-
4.
(1)(x-3)2
=16.
解:
(1)开平方,得
x-3
=±
.
x-3
=±4.
x-3
=
4
或
x-3
=
-
4.
所以,这个方程的解是
x1=7
,
x2=
-1.
(1)(x-3)2
=16.
(x-3)2
=16.
(ax
+
c)2
=
m
(a≠0,m≥0)
开平方
求解
开平方
求解
(2)4(t+4)2=9.
(ax
+
c)2
=
m
(a≠0,m≥0)
(t+4)2=
.
(2)4(t+4)2=9.
解:(2)方程整理,得
开平方,得
所以这个方程的解是
,
.
.
(3)
2(n
-
2-1=0.
(ax
+
c)2
=
m
(a≠0,m≥0)
解:(3)
移项
,得
2(n
-
2=1.
(3)
2(n
-
2-1=0.
解:(3)
移项
,得
2(n
-
2=1.
(3)
2(n
-
2-1=0.
整理,得
(n
-
)2=
.
解:(3)
移项
,得
2(n
-
2=1.
(3)
2(n
-
2-1=0.
整理,得
(n
-
)2=
.
开平方,得
n
-
=±
.
n
-
=±
.
由
,得
.
由
,得
.
所以这个方程的解是
n1=
,
n2=
.
解题步骤
(1)将方程整理成(ax
+
c)2
=
m
(a≠0,m≥0)的形式.
(2)利用开平方法得到两个一元一次方程
(降次).
(3)分别求这两个一元一次方程的解.
(4)这两个一元一次方程的解就是原方程的解.
一元二次方程
一元二次方程
一元二次方程
开平方
降次
一元二次方程
开平方
降次
一元一次方程
一元二次方程
开平方
降次
一元一次方程
一元二次方程
开平方
降次
一元一次方程
求解
一元二次方程
开平方
降次
一元一次方程
求解
x1,
x2
一元二次方程
开平方
降次
一元一次方程
求解
x1,
x2
练习
1.用开平方法解下列方程.
(3)
(3x+1)2
=
7
;
(4)
x2-4x+4
=
9
.
(1)
4x2=81;
(2)
(2x-3)2-25=-9;
(1)
4x2
=81.
解:(1)方程两边同时除以4,得
.
开平方,得
.
所以方程的解是
.
(1)
4x2
=81.
4x2
=
81
解:(2)移项,得
(2x-3)2=-9+25
=16
.
开平方,得
2x-3=±4
.
2x-3=4
或
2x-3=-4
.
所以方程的解是
.
(2)
(2x-3)2-25=-9.
(3)
(3x+1)2
=
7.
开平方,得
.
(3)
(3x+1)2
=
7.
解:(3)两边都乘以
,
(3x+1)2
=
5.
由
,得
.
由
,得
x
=
.
所以这个方程的解是
x1=
,x2=
.
(4)
x2-4x+4=
9.
(4)
x2-4x+4=
9.
解:方程整理,得
(x-2)2=
9.
利用完全平方公式将等号左边进行变形
(4)
x2-4x+4=
9.
解:方程整理,得
(x-2)2=
9.
利用完全平方公式将等号左边进行变形
开平方,得
x-2=±3.
x-2=3
或
x-2=-3.
(4)
x2-4x+4=
9.
解:方程整理,得
(x-2)2=
9.
利用完全平方公式将等号左边进行变形
开平方,得
x-2=±3.
所以这个方程的解是
x1=
5,x2=
-1.
x-2=3
或
x-2=-3.
2.若一元二次方程ax2=
b(a
b>0)的两个解分别是m+1与2m-4,则
=__
.
2.若一元二次方程ax2=
b(a
b>0)的两个解分别是m+1与2m-4,则
=__
.
分析:由ax2=b变形为x2=
,因为a
b>0,所以
>0
,
2.若一元二次方程ax2=
b(a
b>0)的两个解分别是m+1与2m-4,则
=__
.
分析:由ax2=b变形为x2=
,因为a
b>0,所以
>0
,所以方程
x2=
的两个解互为相反数,
2.若一元二次方程ax2=
b(a
b>0)的两个解分别是m+1与2m-4,则
=__
.
分析:由ax2=b变形为x2=
,因为a
b>0,所以
>0
,所以方程
x2=
的两个解互为相反数,
所以m+1+2m-4=0,解得m=1,
2.若一元二次方程ax2=
b(a
b>0)的两个解分别是m+1与2m-4,则
=__
.
分析:由ax2=b变形为x2=
,因为a
b>0,所以
>0
,所以方程
x2=
的两个解互为相反数,
所以m+1+2m-4=0,解得m=1,所以x1=m+1=2,x2=-2,
2.若一元二次方程ax2=
b(a
b>0)的两个解分别是m+1与2m-4,则
=_4_
.
分析:由ax2=b变形为x2=
,因为a
b>0,所以
>0
,所以方程
x2=
的两个解互为相反数,
所以m+1+2m-4=0,解得m=1,所以x1=m+1=2,x2=-2,所以
=4
.
小结
小结
1.形如x2
=
m(m≥0)的方程可以用开平方求出
方程的解,这种解法称为开平方法.
小结
1.形如x2
=
m(m≥0)的方程可以用开平方求出
方程的解,这种解法称为开平方法.
2.方程x2
=
m的解的情况.
?
?
m>0
m
=
0
m<0
方程解的情况
方程解的表示
x1=
x2=0
无解
没有实数解.
两个不相等的实数解,两个解互为相反数.
有两个相等的实数解,两个解都是0.
一元二次方程,有可能有解,也可能无解,有解必有两个.
3.利用开平方法解一元二次方程的一般步骤.
3.利用开平方法解一元二次方程的一般步骤.
(1)将方程整理成x2
=
m或(ax
+
c)2
=
m
(a≠0,m≥0)的形式;
3.利用开平方法解一元二次方程的一般步骤.
(1)将方程整理成x2
=
m或(ax
+
c)2
=
m
(a≠0,m≥0)的形式;
(2)利用开平方法得到两个一元一次方程(降次);
3.利用开平方法解一元二次方程的一般步骤.
(1)将方程整理成x2
=
m或(ax
+
c)2
=
m
(a≠0,m≥0)的形式;
(2)利用开平方法得到两个一元一次方程(降次);
(3)求这两个一元一次方程的解;
3.利用开平方法解一元二次方程的一般步骤.
(1)将方程整理成x2
=
m或(ax
+
c)2
=
m
(a≠0,m≥0)的形式;
(2)利用开平方法得到两个一元一次方程(降次);
(3)求这两个一元一次方程的解;
(4)这两个一元一次方程的解就是原方程的解;
3.利用开平方法解一元二次方程的一般步骤.
(1)将方程整理成x2
=
m或(ax
+
c)2
=
m
(a≠0,m≥0)的形式;
(2)利用开平方法得到两个一元一次方程(降次);
(3)求这两个一元一次方程的解;
(4)这两个一元一次方程的解就是原方程的解;
(5)结果要化简.
A组:1.用开平方法解下列方程.
(1)
x2-289
=
0;
(2)
3x2-75=
0.
B组:2.用开平方法解下列方程.
(1)3(a-1)2-2
=
0;
(2)121-25(y+
2=
0.
作业
祝同学们学习愉快!
同课章节目录
