人教版初二数学下期19.1.2函数图象的表示方法课件(117张ppt)
文档属性
| 名称 | 人教版初二数学下期19.1.2函数图象的表示方法课件(117张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 9.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 22:51:57 | ||
图片预览


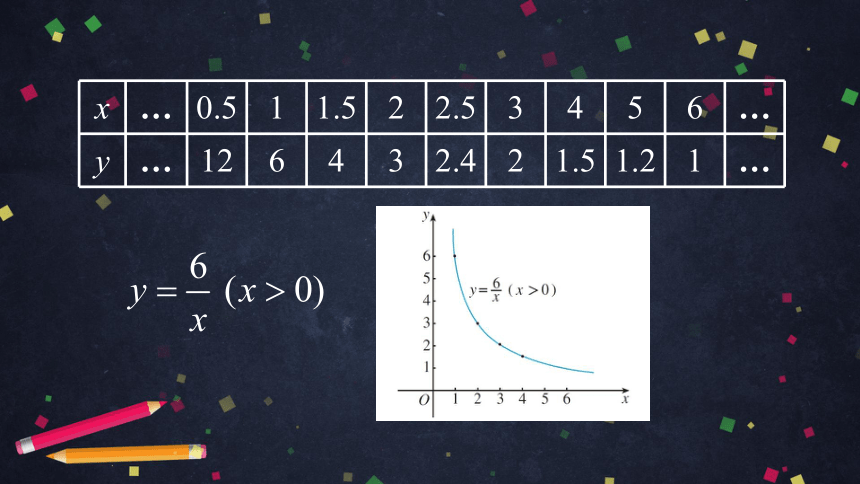

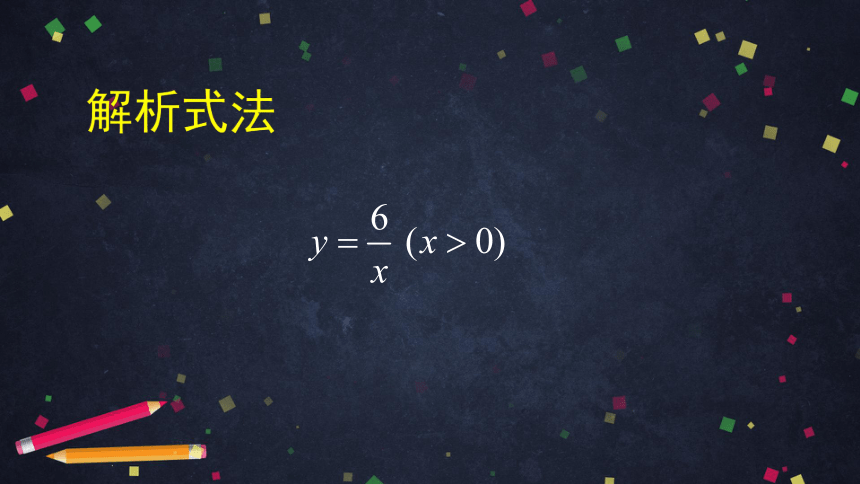


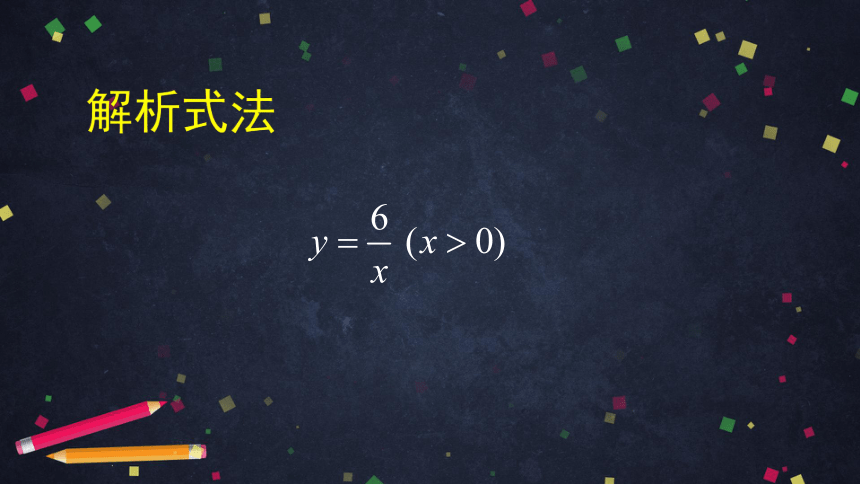

文档简介
(共117张PPT)
初二年级
数学
函数图象的表示方法
课程简介
本课程以探索简单实际问题中的数量关系和变化规律为背景,复习函数的三种表示方法,结合图象数形结合的分析简单的函数关系.提高观察数据的能力以及由所学函数知识推测事物变化趋势的能力.
x
…
0.5
1
1.5
2
2.5
3
4
5
6
…
y
…
12
6
4
3
2.4
2
1.5
1.2
1
…
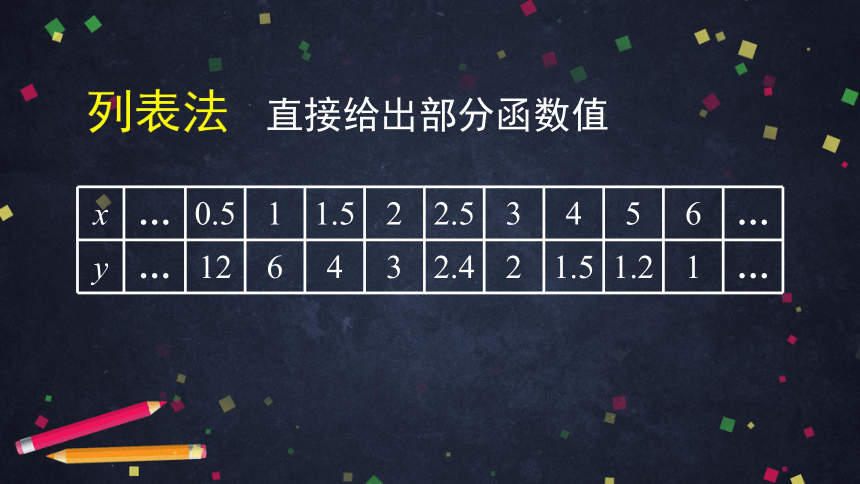
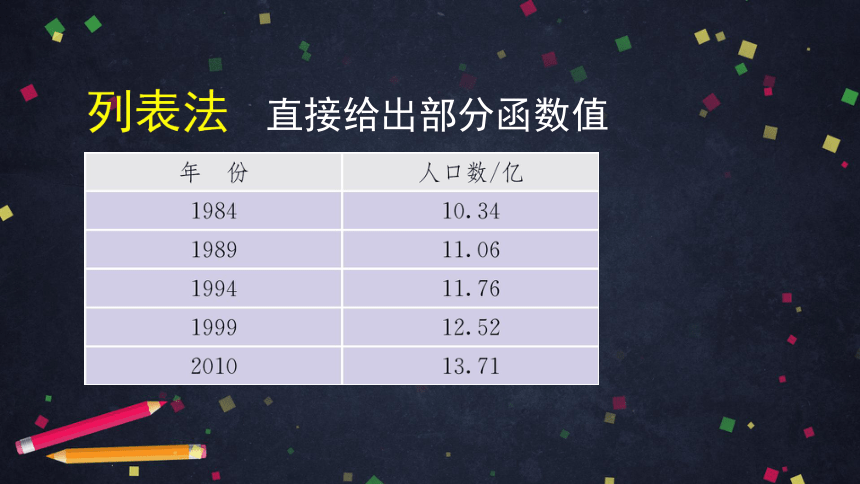
列表法
x
…
0.5
1
1.5
2
2.5
3
4
5
6
…
y
…
12
6
4
3
2.4
2
1.5
1.2
1
…
解析式法
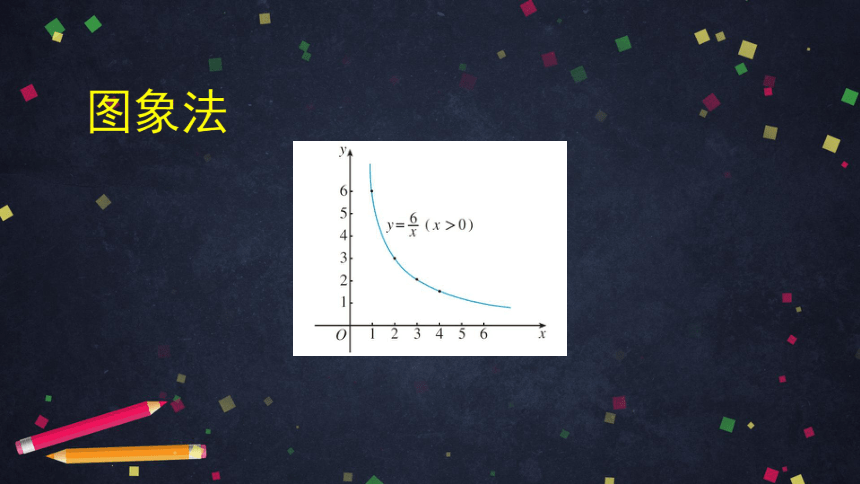
图象法
那么你认为三种表示函数的方法各有什么优点呢?
列表法
解析式法
图象法
列表法
x
…
0.5
1
1.5
2
2.5
3
4
5
6
…
y
…
12
6
4
3
2.4
2
1.5
1.2
1
…
列表法
x
…
0.5
1
1.5
2
2.5
3
4
5
6
…
y
…
12
6
4
3
2.4
2
1.5
1.2
1
…
直接给出部分函数值
列表法
直接给出部分函数值
解析式法
解析式法
明显表示对应数量关系
解析式法
明显表示对应数量关系
图象法
图象法
直观表示变化趋势
图象法
直观表示变化趋势
函数的表示方法
列表法
解析式法
图象法
直接给出部分函数值
直观表示变化趋势
明显表示对应数量关系
例
一个水库的水位在最近
5
h
内持续上涨,表中记录了这
5
h
内
6
个时间点的水位高度,其中
t
表示时间,y
表示水位高度.
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
例
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你能发现水位变化有什么规律吗?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
描出表中数据对应的点,可以看出这
6
个点在一条直线上.
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
描出表中数据对应的点,可以看出这
6
个点在一条直线上.
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)描出表中数据对应的点,可以看出这
6
个点在一条直线上.由此你能发现水位变化还有什么规律吗?
水位变化有什么规律?
水位变化有什么规律?
水位变化有什么规律?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
水位变化有什么规律?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
+0.3
水位变化有什么规律?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
+0.3
+0.3
水位变化有什么规律?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
+0.3
+0.3
+0.3
水位变化有什么规律?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
+0.3
+0.3
+0.3
+0.3
水位变化有什么规律?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
+0.3
+0.3
+0.3
+0.3
+0.3
水位变化有什么规律?
每小时水位上升
0.3
m
水位可能是始终以同一速度均匀上升的.
(2)
水位高度
y
是否为时间
t
的函数?如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
在这个时间段内水位可能是始终以同一速度均匀上升的,每小时上升
0.3
m.
(2)
水位高度
y
是否为时间
t
的函数?如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.
在这个时间段内水位可能是始终以同一速度均匀上升的,每小时上升
0.3
m.
在这个时间段内水位可能是始终以同一速度均匀上升的,每小时上升
0.3
m.
在这个时间段内水位可能是始终以同一速度均匀上升的,每小时上升
0.3
m.
在这个时间段内水位可能是始终以同一速度均匀上升的,每小时上升
0.3
m.
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
函数表示方法:列表法、解析式法、图象法
(3)
据估计这种上涨规律还会持续
2
h,预测再过
2
h
水位高度将为多少米.
(3)
当
时,
即再过
2
h
水位高度为
5.1
m.
(3)
当
时,
即再过
2
h
水位高度为
5.1
m.
练习
食用油沸点的温度远高于水的沸点温度.
小明为了用量程不超过
100℃
的温度计测量出某种食用油沸点的温度,在锅中倒入一些这种食用油,用煤气灶均匀加热,并每隔
10
s
测量一次锅中油温,测量得到的数据如下表:
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
小明还观察到,烧了110
s
时,油沸腾了.你能借助函数的表示方法,估计这种油沸点的温度是多少吗?
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
小明还观察到,烧了110
s
时,油沸腾了.你能借助函数的表示方法,估计这种油沸点的温度是多少吗?
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
当
t
=110
(s)
时,
y
=2×110+10=230
(℃)
即沸点230℃.
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
函数的表示方法
列表法
解析式法
图象法
直接给出部分函数值
直观表示变化趋势
明显表示对应数量关系
例
“漏壶”是一种古代计时器,在它内部盛一定量的水,水从壶下的小孔漏出,壶内壁有刻度,人们根据壶中水面的位置计算时间,用
x
表示漏水时间,y
表示壶底到水面的高度.
(不考虑水量变化对压力的影响)
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
例
漏水时间增加量
0
1
2
3
…
水面高度变化量
-h
-h
-h
…
例
甲
乙
漏水时间增加量
0
1
2
3
…
水面高度变化量
-h
-h
-h
…
例
甲
乙
漏水时间增加量
0
1
2
3
…
水面高度变化量
-h
-h
-h
…
例
甲
乙
漏水时间增加量
0
1
2
3
…
水面高度变化量
-h
-h
-h
…
例
甲
乙
漏水时间增加量
0
1
2
3
…
水面高度变化量
-h
-h
-h
…
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
练习
匀速的向一个容器内注水,最后把容器注满.在注水过程中,水面高度
h
随时间
t
的变化规律如图所示.
练习
这个容器的形状是下图中的哪一个?
练习
这个容器的形状是下图中的哪一个?
缓
练习
这个容器的形状是下图中的哪一个?
缓
练习
这个容器的形状是下图中的哪一个?
缓
练习
这个容器的形状是下图中的哪一个?
缓
练习
这个容器的形状是下图中的哪一个?
缓
慢
粗
练习
这个容器的形状是下图中的哪一个?
缓
慢
粗
细
快
练习
这个容器的形状是下图中的哪一个?
缓
慢
粗
细
快
练习
这个容器的形状是下图中的哪一个?
缓
慢
粗
细
快
你能画出向另外两个容器注水时水面高度关于时间
t
的函数图象草图吗?
用
x
表示漏水时间,y
表示壶底到水面的高度.
用
x
表示漏水时间,y
表示壶底到水面的高度.
课堂小结
(1)函数有哪几种表示方法?这些表示方法分别有哪些优势和不足?
课堂小结
(1)函数有哪几种表示方法?这些表示方法分别有哪些优势和不足?
(2)这些方法之间可以互相转化吗?当我们无法直接得到函数解析式时,可以通过哪些步骤的研究,把握变化规律,预测变化趋势?
课堂小结
函数的表示方法:
列表法
解析式法
图象法
课堂小结
函数的表示方法:
列表法
直接给出部分函数值
解析式法
明显表示对应数量关系
图象法
直观表示变化趋势
课堂小结
函数的表示方法:
作业1
一条小船沿直线向码头匀速前进,在0
min,2
min,4
min,6
min
时,测得小船与码头的距离分别为200
m,150
m,100
m,50
m.
小船与码头的距离
s
是时间
t
的函数吗?如果是,写出函数解析式,并画出函数图象.
如果船速不变,多长时间后小船到达码头?
作业2
通过这节课的学习,你对函数的三种表示方法有什么新的认识和了解呢?找一找,生活中你有没有见过这些表示方法呢?它们都是怎样发挥自己的特长的?请写下你的感受吧.
再
见
初二年级
数学
函数图象的表示方法
课程简介
本课程以探索简单实际问题中的数量关系和变化规律为背景,复习函数的三种表示方法,结合图象数形结合的分析简单的函数关系.提高观察数据的能力以及由所学函数知识推测事物变化趋势的能力.
x
…
0.5
1
1.5
2
2.5
3
4
5
6
…
y
…
12
6
4
3
2.4
2
1.5
1.2
1
…
列表法
x
…
0.5
1
1.5
2
2.5
3
4
5
6
…
y
…
12
6
4
3
2.4
2
1.5
1.2
1
…
解析式法
图象法
那么你认为三种表示函数的方法各有什么优点呢?
列表法
解析式法
图象法
列表法
x
…
0.5
1
1.5
2
2.5
3
4
5
6
…
y
…
12
6
4
3
2.4
2
1.5
1.2
1
…
列表法
x
…
0.5
1
1.5
2
2.5
3
4
5
6
…
y
…
12
6
4
3
2.4
2
1.5
1.2
1
…
直接给出部分函数值
列表法
直接给出部分函数值
解析式法
解析式法
明显表示对应数量关系
解析式法
明显表示对应数量关系
图象法
图象法
直观表示变化趋势
图象法
直观表示变化趋势
函数的表示方法
列表法
解析式法
图象法
直接给出部分函数值
直观表示变化趋势
明显表示对应数量关系
例
一个水库的水位在最近
5
h
内持续上涨,表中记录了这
5
h
内
6
个时间点的水位高度,其中
t
表示时间,y
表示水位高度.
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
例
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你能发现水位变化有什么规律吗?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
描出表中数据对应的点,可以看出这
6
个点在一条直线上.
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)
在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?
描出表中数据对应的点,可以看出这
6
个点在一条直线上.
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
(1)描出表中数据对应的点,可以看出这
6
个点在一条直线上.由此你能发现水位变化还有什么规律吗?
水位变化有什么规律?
水位变化有什么规律?
水位变化有什么规律?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
水位变化有什么规律?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
+0.3
水位变化有什么规律?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
+0.3
+0.3
水位变化有什么规律?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
+0.3
+0.3
+0.3
水位变化有什么规律?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
+0.3
+0.3
+0.3
+0.3
水位变化有什么规律?
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
+0.3
+0.3
+0.3
+0.3
+0.3
水位变化有什么规律?
每小时水位上升
0.3
m
水位可能是始终以同一速度均匀上升的.
(2)
水位高度
y
是否为时间
t
的函数?如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
在这个时间段内水位可能是始终以同一速度均匀上升的,每小时上升
0.3
m.
(2)
水位高度
y
是否为时间
t
的函数?如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.
在这个时间段内水位可能是始终以同一速度均匀上升的,每小时上升
0.3
m.
在这个时间段内水位可能是始终以同一速度均匀上升的,每小时上升
0.3
m.
在这个时间段内水位可能是始终以同一速度均匀上升的,每小时上升
0.3
m.
在这个时间段内水位可能是始终以同一速度均匀上升的,每小时上升
0.3
m.
t
/
h
0
1
2
3
4
5
y
/
m
3
3.3
3.6
3.9
4.2
4.5
函数表示方法:列表法、解析式法、图象法
(3)
据估计这种上涨规律还会持续
2
h,预测再过
2
h
水位高度将为多少米.
(3)
当
时,
即再过
2
h
水位高度为
5.1
m.
(3)
当
时,
即再过
2
h
水位高度为
5.1
m.
练习
食用油沸点的温度远高于水的沸点温度.
小明为了用量程不超过
100℃
的温度计测量出某种食用油沸点的温度,在锅中倒入一些这种食用油,用煤气灶均匀加热,并每隔
10
s
测量一次锅中油温,测量得到的数据如下表:
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
小明还观察到,烧了110
s
时,油沸腾了.你能借助函数的表示方法,估计这种油沸点的温度是多少吗?
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
小明还观察到,烧了110
s
时,油沸腾了.你能借助函数的表示方法,估计这种油沸点的温度是多少吗?
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
当
t
=110
(s)
时,
y
=2×110+10=230
(℃)
即沸点230℃.
练习
时间
t
/
s
0
10
20
30
40
油温
y
/
℃
10
30
50
70
90
函数的表示方法
列表法
解析式法
图象法
直接给出部分函数值
直观表示变化趋势
明显表示对应数量关系
例
“漏壶”是一种古代计时器,在它内部盛一定量的水,水从壶下的小孔漏出,壶内壁有刻度,人们根据壶中水面的位置计算时间,用
x
表示漏水时间,y
表示壶底到水面的高度.
(不考虑水量变化对压力的影响)
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
例
漏水时间增加量
0
1
2
3
…
水面高度变化量
-h
-h
-h
…
例
甲
乙
漏水时间增加量
0
1
2
3
…
水面高度变化量
-h
-h
-h
…
例
甲
乙
漏水时间增加量
0
1
2
3
…
水面高度变化量
-h
-h
-h
…
例
甲
乙
漏水时间增加量
0
1
2
3
…
水面高度变化量
-h
-h
-h
…
例
甲
乙
漏水时间增加量
0
1
2
3
…
水面高度变化量
-h
-h
-h
…
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
4
14
例
用
x
表示漏水时间,y
表示壶底到水面的高度.
练习
匀速的向一个容器内注水,最后把容器注满.在注水过程中,水面高度
h
随时间
t
的变化规律如图所示.
练习
这个容器的形状是下图中的哪一个?
练习
这个容器的形状是下图中的哪一个?
缓
练习
这个容器的形状是下图中的哪一个?
缓
练习
这个容器的形状是下图中的哪一个?
缓
练习
这个容器的形状是下图中的哪一个?
缓
练习
这个容器的形状是下图中的哪一个?
缓
慢
粗
练习
这个容器的形状是下图中的哪一个?
缓
慢
粗
细
快
练习
这个容器的形状是下图中的哪一个?
缓
慢
粗
细
快
练习
这个容器的形状是下图中的哪一个?
缓
慢
粗
细
快
你能画出向另外两个容器注水时水面高度关于时间
t
的函数图象草图吗?
用
x
表示漏水时间,y
表示壶底到水面的高度.
用
x
表示漏水时间,y
表示壶底到水面的高度.
课堂小结
(1)函数有哪几种表示方法?这些表示方法分别有哪些优势和不足?
课堂小结
(1)函数有哪几种表示方法?这些表示方法分别有哪些优势和不足?
(2)这些方法之间可以互相转化吗?当我们无法直接得到函数解析式时,可以通过哪些步骤的研究,把握变化规律,预测变化趋势?
课堂小结
函数的表示方法:
列表法
解析式法
图象法
课堂小结
函数的表示方法:
列表法
直接给出部分函数值
解析式法
明显表示对应数量关系
图象法
直观表示变化趋势
课堂小结
函数的表示方法:
作业1
一条小船沿直线向码头匀速前进,在0
min,2
min,4
min,6
min
时,测得小船与码头的距离分别为200
m,150
m,100
m,50
m.
小船与码头的距离
s
是时间
t
的函数吗?如果是,写出函数解析式,并画出函数图象.
如果船速不变,多长时间后小船到达码头?
作业2
通过这节课的学习,你对函数的三种表示方法有什么新的认识和了解呢?找一找,生活中你有没有见过这些表示方法呢?它们都是怎样发挥自己的特长的?请写下你的感受吧.
再
见
