沪教版(上海)九年级第一学期 24.1 放缩与相似形课件 (共22张PPT)
文档属性
| 名称 | 沪教版(上海)九年级第一学期 24.1 放缩与相似形课件 (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
学习数学有什么用?
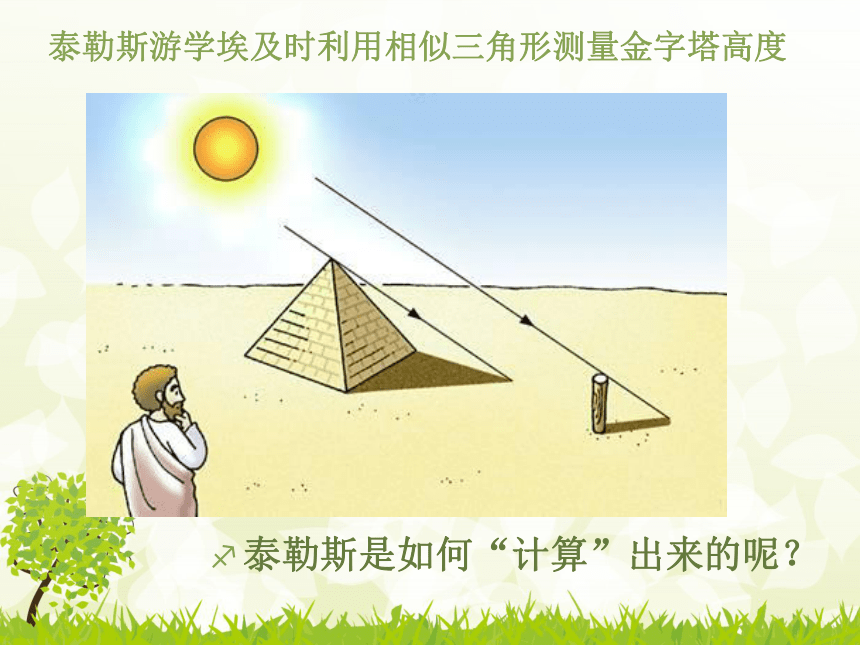
泰勒斯游学埃及时利用相似三角形测量金字塔高度
泰勒斯是如何“计算”出来的呢?
24.1放缩与相似形
第二十四章
相似三角形
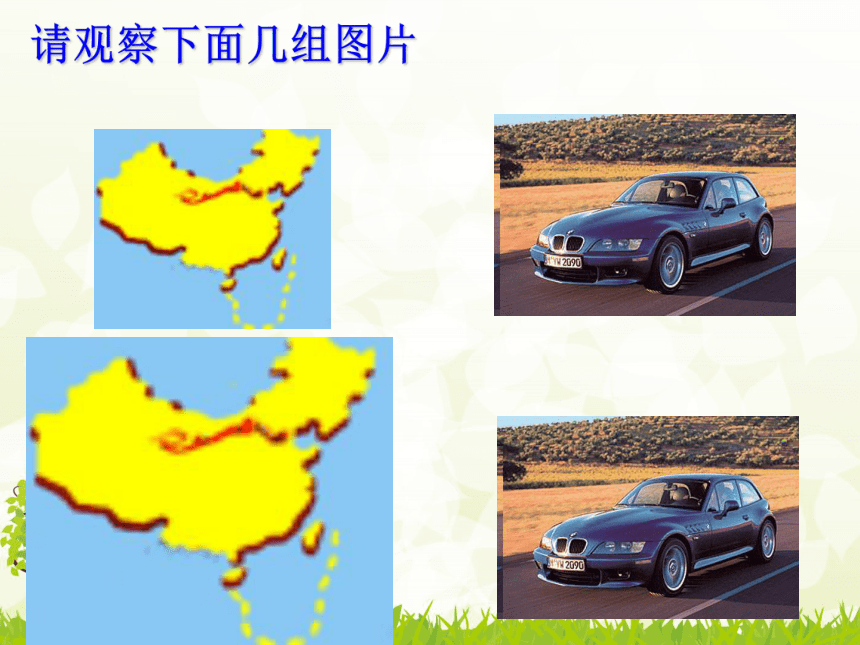
请观察下面几组图片
请观察下面几组图片
请观察下面几组图片
请观察下面几组图片
你从上述几组图片发现了什么?
它们的大小不一定相等,
形状相同.
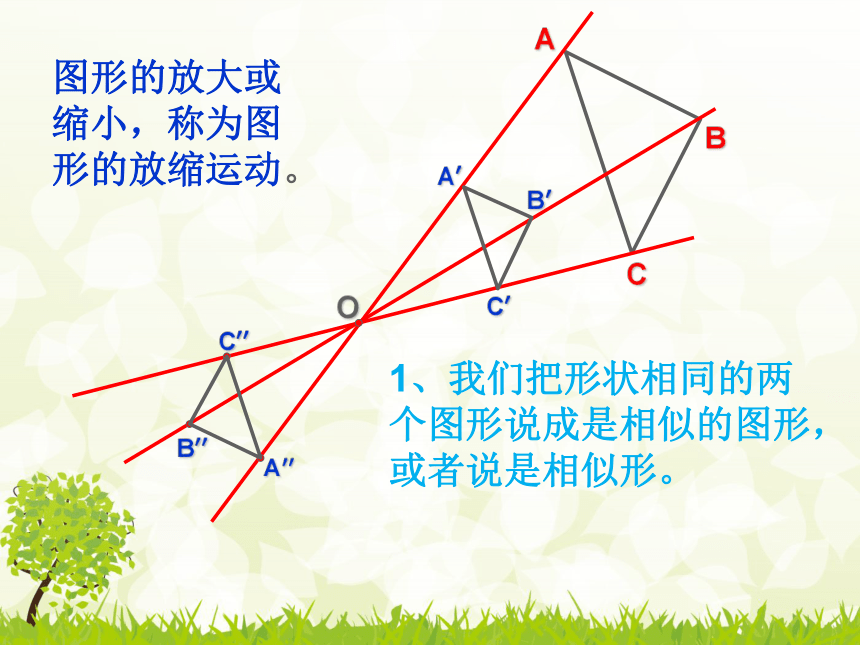
O
A
B
C
A′′
B′′
C′′
A′
B′
C′
图形的放大或缩小,称为图形的放缩运动。
1、我们把形状相同的两个图形说成是相似的图形,或者说是相似形。
形状、大小都相同的图形称为全等图形。
2、全等图形:
注:全等图形是相似图形的特殊情况。
想一想:
下列图形中,能确定相似的有(
)
A、两个半径不相等的圆
B、所有的等边三角形
C、所有的等腰三角形
D、所有的正方形
E、所有的等腰梯形
F、所有的正六边形
B
A
F
D
猜测:
如果两个图形相似,它们的对应边、对应角可能存在某种关系.
两个相似的平面图形之间有什么关系呢?为什么有些图形是相似的,而有些不是呢?相似图形有什么主要特征呢?
(1)如图所示的两个四边形是否相似?
基础训练
(2)如图,正方形的边长a=10,菱形的
边长b=5,它们相似吗?请说明理由.
基础训练
如果两个多边形相似,那么它们的对应角有什么关系?对应边呢?
相似多边形的对应角相等,对应边成比例
相似多边形的性质1:
符号语言(以四边形为例):
∵四边形ABCD与四边形A′B′C′D′相似
(如果两个多边形是相似形,
那么这两个多边形的
对应角相等对应边成比例,)
例1:在如图所示的相似四边形中,
求未知边x、
y的长度和角度a的大小.
解:由于两个四边形相似,它们的对应边成比例,对应角相等,所以
解得
x=31.5,y=27
a
=360°-(77°+83°+117°)=83°
放缩运动
图形相似的性质
相似形
相似多边形
特征
识别
对应角相等
对应边成比例
相似多边形的特征和识别:
小结:
再见
学习数学有什么用?
泰勒斯游学埃及时利用相似三角形测量金字塔高度
泰勒斯是如何“计算”出来的呢?
24.1放缩与相似形
第二十四章
相似三角形
请观察下面几组图片
请观察下面几组图片
请观察下面几组图片
请观察下面几组图片
你从上述几组图片发现了什么?
它们的大小不一定相等,
形状相同.
O
A
B
C
A′′
B′′
C′′
A′
B′
C′
图形的放大或缩小,称为图形的放缩运动。
1、我们把形状相同的两个图形说成是相似的图形,或者说是相似形。
形状、大小都相同的图形称为全等图形。
2、全等图形:
注:全等图形是相似图形的特殊情况。
想一想:
下列图形中,能确定相似的有(
)
A、两个半径不相等的圆
B、所有的等边三角形
C、所有的等腰三角形
D、所有的正方形
E、所有的等腰梯形
F、所有的正六边形
B
A
F
D
猜测:
如果两个图形相似,它们的对应边、对应角可能存在某种关系.
两个相似的平面图形之间有什么关系呢?为什么有些图形是相似的,而有些不是呢?相似图形有什么主要特征呢?
(1)如图所示的两个四边形是否相似?
基础训练
(2)如图,正方形的边长a=10,菱形的
边长b=5,它们相似吗?请说明理由.
基础训练
如果两个多边形相似,那么它们的对应角有什么关系?对应边呢?
相似多边形的对应角相等,对应边成比例
相似多边形的性质1:
符号语言(以四边形为例):
∵四边形ABCD与四边形A′B′C′D′相似
(如果两个多边形是相似形,
那么这两个多边形的
对应角相等对应边成比例,)
例1:在如图所示的相似四边形中,
求未知边x、
y的长度和角度a的大小.
解:由于两个四边形相似,它们的对应边成比例,对应角相等,所以
解得
x=31.5,y=27
a
=360°-(77°+83°+117°)=83°
放缩运动
图形相似的性质
相似形
相似多边形
特征
识别
对应角相等
对应边成比例
相似多边形的特征和识别:
小结:
再见
