湖北省黄冈地区中考数学专题辅导(1 )—(3)(1有理数与实数、2代数式 整式与分式、3方程与方程组)人教
文档属性
| 名称 | 湖北省黄冈地区中考数学专题辅导(1 )—(3)(1有理数与实数、2代数式 整式与分式、3方程与方程组)人教 | 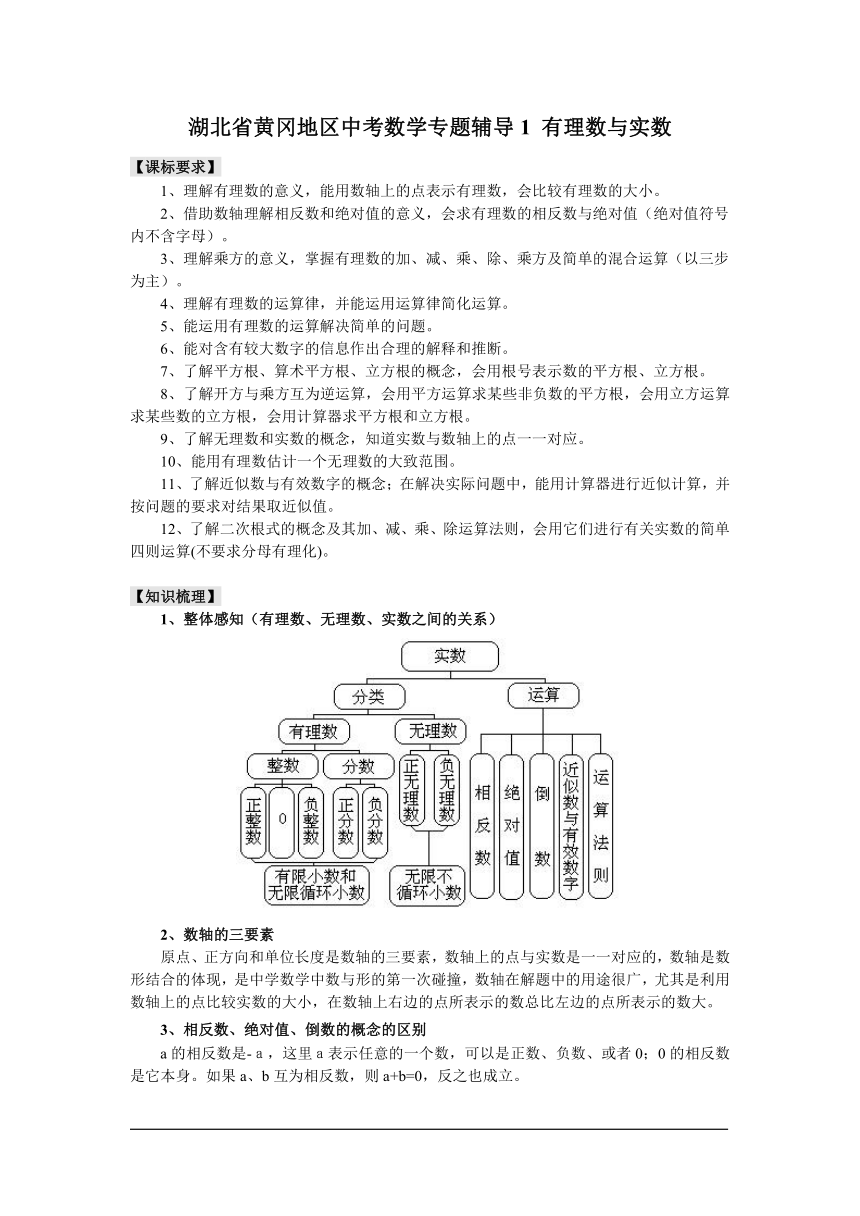 | |
| 格式 | zip | ||
| 文件大小 | 101.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-02-13 21:00:00 | ||
图片预览


文档简介
湖北省黄冈地区中考数学专题辅导1 有理数与实数
【课标要求】
1、理解有理数的意义,能用数轴上的点表示有理数,会比较有理数的大小。
2、借助数轴理解相反数和绝对值的意义,会求有理数的相反数与绝对值(绝对值符号内不含字母)。
3、理解乘方的意义,掌握有理数的加、减、乘、除、乘方及简单的混合运算(以三步为主)。
4、理解有理数的运算律,并能运用运算律简化运算。
5、能运用有理数的运算解决简单的问题。
6、能对含有较大数字的信息作出合理的解释和推断。
7、了解平方根、算术平方根、立方根的概念,会用根号表示数的平方根、立方根。
8、了解开方与乘方互为逆运算,会用平方运算求某些非负数的平方根,会用立方运算求某些数的立方根,会用计算器求平方根和立方根。
9、了解无理数和实数的概念,知道实数与数轴上的点一一对应。
10、能用有理数估计一个无理数的大致范围。
11、了解近似数与有效数字的概念;在解决实际问题中,能用计算器进行近似计算,并按问题的要求对结果取近似值。
12、了解二次根式的概念及其加、减、乘、除运算法则,会用它们进行有关实数的简单四则运算(不要求分母有理化)。
【知识梳理】
1、整体感知(有理数、无理数、实数之间的关系)
2、数轴的三要素
原点、正方向和单位长度是数轴的三要素,数轴上的点与实数是一一对应的,数轴是数形结合的体现,是中学数学中数与形的第一次碰撞,数轴在解题中的用途很广,尤其是利用数轴上的点比较实数的大小,在数轴上右边的点所表示的数总比左边的点所表示的数大。
3、相反数、绝对值、倒数的概念的区别
a的相反数是-a,这里a表示任意的一个数,可以是正数、负数、或者0;0的相反数是它本身。如果a、b互为相反数,则a+b=0,反之也成立。
a(a≠0)的倒数是,0没有倒数,倒数等于本身的数是1和-1。如果a、b互为倒数,则ab=1,反之也成立。
一个数a的绝对值就是数轴上表示数a的点到原点的距离,记作|a|,当a≥0时,|a|=a,当a<0时,|a|=-a.
4、实数的运算法则及运算率
在实数范围内可以进行加、减、乘、除、乘方和开方的运算,其中零不能做除数,负数不能开方。有理数的运算律和一切运算性质一样在实数运算中同样适用。特别地,a0=1(a≠0),a-1=(a≠0,且n是正整数)。
5、平方根、算术平方根和立方根
正数a的平方根有两个。 即±,它们互为相反数。0的平方根是0;负数没有平方根。算术平方根是指一个数正的平方根,0的算术平方根是它的本身。
立方根:一个正数只有一个正的立方根,而负数有一个负的立方根,立方根等于自身的数是0和±1。
6、二次根式及运算
形如≥0(a≥0)的式子称为二次根式,其加减法与多项式的加减法类似,其乘法运算有以下公式:·=(a≥0,b≥0),(a≥0,b>0)。
三类形式的非负数:即a≥0,|a|≥0,≥0(a≥0)。非负数有如下的性质:若干个非负数的和仍是非负数;非负数有最小值0;若干个非负数的和为0 ,则每个非负数均为0。
7、近似数、有效数字和科学记数法
一般的,一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位。一个近似数,从左边第一个非零数字起,直到精确到的数字止,所有数字都叫做这个近似数的有效数字。把一个数写成a×10 n 的形式(其中1≤a<10,n是整数),这种记数方法叫做科学记数法。
【热点解析】
实数是初中数学的基础知识,也是其他学科的重要工具。因此在近年来各地的中考试题中一直占有重要的地位。这部分试题大多数十分重视基础知识的考察,试题的呈现形式多以贴近生活实际的形式,试题的难度不大。多数来源于教材的习题或稍加变通。题型主要是填空题、选择题也有计算题,但是,计算题的难度不大,没有繁杂的计算。近几年来,部分地区还设计了开放性探索题。这部分的试题量一般占试题总量的2%~6%,分值占总分的3%~5%。
例1:(2005年吉林省)某食品包装袋上标有“净含量385克±5克”,这包食品的合格净含量范围是 380 克~390克。
分析:能否正确解答此题,关键是对“净含量”的含义的理解。
简解:这包食品的合格净含量范围是380 克~390克。
点评:本题以现实生活中学生非常熟悉的事实题材,不但考察学生对正数、负数以及对具有相反意义的量的理解和掌握,而且考察学生对负数的产生、发展与应用的认识与理解。
例2:(2005年江西省)如下图所示,按下列方法将数轴的正半轴绕在一个圆上(该圆周长为3个单位长,且在圆周的三等分点处分别标上了数字0、1、2)上:先让原点与圆周上0所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上1、2、3、4、…所对应的点分别与圆周上1、2、0、1、…所对应的点重合。这样,正半轴上的整数就与圆周上的数字建立了一种对应关系。
(1)圆周上数字a 与数轴上的数5对应,则a=_________;
(2)数轴上的一个整数点刚刚绕过圆周n圈(n为正整数)后,并落在圆周上数字1所对应的位置,这个整数是_________(用含n的代数式表示)。
分析:本题主要考察阅读理解和规律探索以及归纳概括的能力。
简解:(1)圆周上数字a 与数轴上的数5对应,则a=2;
(2)数轴上的一个整数点刚刚绕过圆周n圈(n为正整数)后,并落在圆周上数字1所对应的位置,这个整数是3n+1。
点评:本题灵活巧妙的将有理数与数轴的一一对应关系自然贴切与数字的规律探索问题有机的结合在一起。充分的体现了数形结合的思想。本题的命题方式新颖、独特,富有创新性和探索性。
例3:(2004年海口)在下面等式的□内填数,○内填运算符号,使等号成立(两个算式中的运算符号不能相同)。
□ ○ □=-6; □ ○ □=-6。
分析:由于题中条件是开放的,可以先在一个□内任填一个数,在再○内任填一个运算符号,另一个□内的数就可以求出了。
简解:答案不唯一,符合条件即可。如-2-4=-6等。
点评:本题灵活考查实数的运算知识,这种开放性题型已成为形课标下中考命题的一种时尚。
例4:已知a>0,且a2=68,你估计a的值在整数 和 之间。
分析:因为a2=68,且a>0,所以a=,而64<68<81,所以8<<9。
简解:8与9。
点评:本题考查了用有理数估计无理数大小的知识,估算是新课标要求学生必须具备的一种能力。
【实战演练】
1、(2005年盐成市)—3的绝对值是 ( )
A.3 B.3 C.1/3 D.—1/3
2、(2005年日照市)2m、m、1—m这三个实数在数轴上所对应的点从左到右依次排列,那么m的取值范围是 ( )
A.m>0 B.m> C.m<0 D.0<m<
3、(2005年南京市)9 的算术平方根是 ( )
A.—3 B.3 C.±3 D.81
4、(2005年日照市)一粒废旧纽扣电池可以使600吨水受到污染.某校团委四年来共回收废旧纽扣电池3500粒.若这3500粒废旧纽扣电池可以使m吨水受到污染,用科学记数法表示m为 ( )
A、2.1×105 B、2.1×10-5m C、2.1×106m D、2.1×10-6m
5、(2005年南京市)√10在两个连续整数a和b之间,a<√10<b,那么a,b的值分别是 。
6、(2005年日照市).已知下列等式:
① 13=12;
② 13+23=32;
③ 13+23+33=62;
④ 13+23+33+43=102 ; …… ……
由此规律知,第⑤个等式是 .
7、(2005年兰州省)观察下列等式(等式中的“!”是一种数学运算符号),
1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,…
计算:=_____
8、(2005年济宁)一个班共有44人,全部报名参加了学校组织的兴趣活动小组,参加数学兴趣活动小组
的有38人,参加物理兴趣活动小组的有35人,则既参加数学兴趣活动小组又参加物理
活动兴趣小组的有 人.
9、(2005年深圳省)在实数a、b在数轴上的位置如图所示,那么化简|a-b|-的结果是
A、2a-b B、b C、-b D、-2a+b
10、(2005年浙江)据了解,火车票价按“”的方法来确定.已知A站至H站总里程数为1 500千米,全程参考价为180元.下表是沿途各站至H站的里程数:
车站名 A B C D E F G H
各站至H站的里程数(单位:千米) 1500 1130 910 622 402 219 72 0
例如,要确定从B站至E站火车票价,其票价为(元).
(1) 求A站至F站的火车票价(结果精确到1元);
(2) 旅客王大妈乘火车去女儿家,上车过两站后拿着火车票问乘务员:我快到站了吗?乘务员看到王大妈手中票价是66元,马上说下一站就到了.请问王大妈是在哪一站下车的?(要求写出解答过程).
【方法导引】
中考首先考察基础知识和基本技能。因此,在复习时一定要从基础知识入手,理清知识网络,不要某些复习资料中的难题、偏题和怪题。要以教材中的习题、练习题为素材和源本结合现实生活进行适当的变形和延伸,从而融会贯通地掌握基础知识。
实数部分的概念比较多,易混易错,在复习时注意掌握和理解概念的性质;实数的计算是最基本的,也是最容易被忽视的问题,在复习时要特别注意计算的正确性,尤其是零指数幂、负整数指数幂的运算;注意对较大的数和较小的数取近似值,以及用科学技术法表示的理解和运用;加强对绝对值、非负数等题型的强化训练;二次根式的运算要注意法则和公式成立的条件,常与有理数的运算、三角函数知识综合在一起以计算题形式在中考中出现。
新课标下的中考题材特别关注生产、生活,从而常会先给出一定的情景,要求考生从实际问题中抽象出关于有理数运算问题,考察学生综合运用数学知识的能力。
b
O
a
【课标要求】
1、理解有理数的意义,能用数轴上的点表示有理数,会比较有理数的大小。
2、借助数轴理解相反数和绝对值的意义,会求有理数的相反数与绝对值(绝对值符号内不含字母)。
3、理解乘方的意义,掌握有理数的加、减、乘、除、乘方及简单的混合运算(以三步为主)。
4、理解有理数的运算律,并能运用运算律简化运算。
5、能运用有理数的运算解决简单的问题。
6、能对含有较大数字的信息作出合理的解释和推断。
7、了解平方根、算术平方根、立方根的概念,会用根号表示数的平方根、立方根。
8、了解开方与乘方互为逆运算,会用平方运算求某些非负数的平方根,会用立方运算求某些数的立方根,会用计算器求平方根和立方根。
9、了解无理数和实数的概念,知道实数与数轴上的点一一对应。
10、能用有理数估计一个无理数的大致范围。
11、了解近似数与有效数字的概念;在解决实际问题中,能用计算器进行近似计算,并按问题的要求对结果取近似值。
12、了解二次根式的概念及其加、减、乘、除运算法则,会用它们进行有关实数的简单四则运算(不要求分母有理化)。
【知识梳理】
1、整体感知(有理数、无理数、实数之间的关系)
2、数轴的三要素
原点、正方向和单位长度是数轴的三要素,数轴上的点与实数是一一对应的,数轴是数形结合的体现,是中学数学中数与形的第一次碰撞,数轴在解题中的用途很广,尤其是利用数轴上的点比较实数的大小,在数轴上右边的点所表示的数总比左边的点所表示的数大。
3、相反数、绝对值、倒数的概念的区别
a的相反数是-a,这里a表示任意的一个数,可以是正数、负数、或者0;0的相反数是它本身。如果a、b互为相反数,则a+b=0,反之也成立。
a(a≠0)的倒数是,0没有倒数,倒数等于本身的数是1和-1。如果a、b互为倒数,则ab=1,反之也成立。
一个数a的绝对值就是数轴上表示数a的点到原点的距离,记作|a|,当a≥0时,|a|=a,当a<0时,|a|=-a.
4、实数的运算法则及运算率
在实数范围内可以进行加、减、乘、除、乘方和开方的运算,其中零不能做除数,负数不能开方。有理数的运算律和一切运算性质一样在实数运算中同样适用。特别地,a0=1(a≠0),a-1=(a≠0,且n是正整数)。
5、平方根、算术平方根和立方根
正数a的平方根有两个。 即±,它们互为相反数。0的平方根是0;负数没有平方根。算术平方根是指一个数正的平方根,0的算术平方根是它的本身。
立方根:一个正数只有一个正的立方根,而负数有一个负的立方根,立方根等于自身的数是0和±1。
6、二次根式及运算
形如≥0(a≥0)的式子称为二次根式,其加减法与多项式的加减法类似,其乘法运算有以下公式:·=(a≥0,b≥0),(a≥0,b>0)。
三类形式的非负数:即a≥0,|a|≥0,≥0(a≥0)。非负数有如下的性质:若干个非负数的和仍是非负数;非负数有最小值0;若干个非负数的和为0 ,则每个非负数均为0。
7、近似数、有效数字和科学记数法
一般的,一个近似数四舍五入到哪一位,就说这个近似数精确到哪一位。一个近似数,从左边第一个非零数字起,直到精确到的数字止,所有数字都叫做这个近似数的有效数字。把一个数写成a×10 n 的形式(其中1≤a<10,n是整数),这种记数方法叫做科学记数法。
【热点解析】
实数是初中数学的基础知识,也是其他学科的重要工具。因此在近年来各地的中考试题中一直占有重要的地位。这部分试题大多数十分重视基础知识的考察,试题的呈现形式多以贴近生活实际的形式,试题的难度不大。多数来源于教材的习题或稍加变通。题型主要是填空题、选择题也有计算题,但是,计算题的难度不大,没有繁杂的计算。近几年来,部分地区还设计了开放性探索题。这部分的试题量一般占试题总量的2%~6%,分值占总分的3%~5%。
例1:(2005年吉林省)某食品包装袋上标有“净含量385克±5克”,这包食品的合格净含量范围是 380 克~390克。
分析:能否正确解答此题,关键是对“净含量”的含义的理解。
简解:这包食品的合格净含量范围是380 克~390克。
点评:本题以现实生活中学生非常熟悉的事实题材,不但考察学生对正数、负数以及对具有相反意义的量的理解和掌握,而且考察学生对负数的产生、发展与应用的认识与理解。
例2:(2005年江西省)如下图所示,按下列方法将数轴的正半轴绕在一个圆上(该圆周长为3个单位长,且在圆周的三等分点处分别标上了数字0、1、2)上:先让原点与圆周上0所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上1、2、3、4、…所对应的点分别与圆周上1、2、0、1、…所对应的点重合。这样,正半轴上的整数就与圆周上的数字建立了一种对应关系。
(1)圆周上数字a 与数轴上的数5对应,则a=_________;
(2)数轴上的一个整数点刚刚绕过圆周n圈(n为正整数)后,并落在圆周上数字1所对应的位置,这个整数是_________(用含n的代数式表示)。
分析:本题主要考察阅读理解和规律探索以及归纳概括的能力。
简解:(1)圆周上数字a 与数轴上的数5对应,则a=2;
(2)数轴上的一个整数点刚刚绕过圆周n圈(n为正整数)后,并落在圆周上数字1所对应的位置,这个整数是3n+1。
点评:本题灵活巧妙的将有理数与数轴的一一对应关系自然贴切与数字的规律探索问题有机的结合在一起。充分的体现了数形结合的思想。本题的命题方式新颖、独特,富有创新性和探索性。
例3:(2004年海口)在下面等式的□内填数,○内填运算符号,使等号成立(两个算式中的运算符号不能相同)。
□ ○ □=-6; □ ○ □=-6。
分析:由于题中条件是开放的,可以先在一个□内任填一个数,在再○内任填一个运算符号,另一个□内的数就可以求出了。
简解:答案不唯一,符合条件即可。如-2-4=-6等。
点评:本题灵活考查实数的运算知识,这种开放性题型已成为形课标下中考命题的一种时尚。
例4:已知a>0,且a2=68,你估计a的值在整数 和 之间。
分析:因为a2=68,且a>0,所以a=,而64<68<81,所以8<<9。
简解:8与9。
点评:本题考查了用有理数估计无理数大小的知识,估算是新课标要求学生必须具备的一种能力。
【实战演练】
1、(2005年盐成市)—3的绝对值是 ( )
A.3 B.3 C.1/3 D.—1/3
2、(2005年日照市)2m、m、1—m这三个实数在数轴上所对应的点从左到右依次排列,那么m的取值范围是 ( )
A.m>0 B.m> C.m<0 D.0<m<
3、(2005年南京市)9 的算术平方根是 ( )
A.—3 B.3 C.±3 D.81
4、(2005年日照市)一粒废旧纽扣电池可以使600吨水受到污染.某校团委四年来共回收废旧纽扣电池3500粒.若这3500粒废旧纽扣电池可以使m吨水受到污染,用科学记数法表示m为 ( )
A、2.1×105 B、2.1×10-5m C、2.1×106m D、2.1×10-6m
5、(2005年南京市)√10在两个连续整数a和b之间,a<√10<b,那么a,b的值分别是 。
6、(2005年日照市).已知下列等式:
① 13=12;
② 13+23=32;
③ 13+23+33=62;
④ 13+23+33+43=102 ; …… ……
由此规律知,第⑤个等式是 .
7、(2005年兰州省)观察下列等式(等式中的“!”是一种数学运算符号),
1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,…
计算:=_____
8、(2005年济宁)一个班共有44人,全部报名参加了学校组织的兴趣活动小组,参加数学兴趣活动小组
的有38人,参加物理兴趣活动小组的有35人,则既参加数学兴趣活动小组又参加物理
活动兴趣小组的有 人.
9、(2005年深圳省)在实数a、b在数轴上的位置如图所示,那么化简|a-b|-的结果是
A、2a-b B、b C、-b D、-2a+b
10、(2005年浙江)据了解,火车票价按“”的方法来确定.已知A站至H站总里程数为1 500千米,全程参考价为180元.下表是沿途各站至H站的里程数:
车站名 A B C D E F G H
各站至H站的里程数(单位:千米) 1500 1130 910 622 402 219 72 0
例如,要确定从B站至E站火车票价,其票价为(元).
(1) 求A站至F站的火车票价(结果精确到1元);
(2) 旅客王大妈乘火车去女儿家,上车过两站后拿着火车票问乘务员:我快到站了吗?乘务员看到王大妈手中票价是66元,马上说下一站就到了.请问王大妈是在哪一站下车的?(要求写出解答过程).
【方法导引】
中考首先考察基础知识和基本技能。因此,在复习时一定要从基础知识入手,理清知识网络,不要某些复习资料中的难题、偏题和怪题。要以教材中的习题、练习题为素材和源本结合现实生活进行适当的变形和延伸,从而融会贯通地掌握基础知识。
实数部分的概念比较多,易混易错,在复习时注意掌握和理解概念的性质;实数的计算是最基本的,也是最容易被忽视的问题,在复习时要特别注意计算的正确性,尤其是零指数幂、负整数指数幂的运算;注意对较大的数和较小的数取近似值,以及用科学技术法表示的理解和运用;加强对绝对值、非负数等题型的强化训练;二次根式的运算要注意法则和公式成立的条件,常与有理数的运算、三角函数知识综合在一起以计算题形式在中考中出现。
新课标下的中考题材特别关注生产、生活,从而常会先给出一定的情景,要求考生从实际问题中抽象出关于有理数运算问题,考察学生综合运用数学知识的能力。
b
O
a
同课章节目录
