人教新版七年级数学下册 5.3 平行线的性质 同步练习(含答案)
文档属性
| 名称 | 人教新版七年级数学下册 5.3 平行线的性质 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 121.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-07 19:34:21 | ||
图片预览


文档简介
5.3
平行线的性质
一.选择题(共8小题,满分24分,每小题3分)
1.已知直线a∥b,点M到直线a的距离是6cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为( )
A.3
cm
B.9
cm
C.3
cm或9
cm
D.6
cm
2.下列语句是命题的为( )
A.作直线AB的垂线
B.同角的余角相等吗?
C.延长线段AO到C,使OC=OA
D.两直线相交,只有一个交点
3.下列三个命题:①同角的补角相等;②如果b∥a,c∥a,那么b∥c;③如果一个角的两边分别平行于另一个角的两边,那么这两个角相等,其中是真命题的有( )
A.0个
B.1个
C.2个
D.3个
4.说明“如果x<2,那么x2<4”是假命题,可以举一个反例x的值为( )
A.﹣1
B.﹣3
C.0
D.1.5
5.小明中午放学回家自己煮面条吃,有下面几道工序:(1)洗锅盛水2分钟;(2)洗菜3分钟;(3)准备面条及佐料2分钟;(4)用锅把水烧开7分钟;(5)用烧开的水煮面条和菜要3分钟.以上各工序除(4)外,一次只能进行一道工序,小明要将面条煮好,最少用( )
A.14分钟
B.13分钟
C.12分钟
D.11分钟
6.某旅行团在一城市游览,有甲、乙、丙、丁四个景点,导游说:“①要游览甲,就得去乙;②乙、丙只能去一个;③丙、丁要么都去,要么都不去;”根据导游的说法,在下列选项中,该旅行团可能游览的景点是( )
A.甲、丙
B.甲、丁
C.乙、丁
D.丙、丁
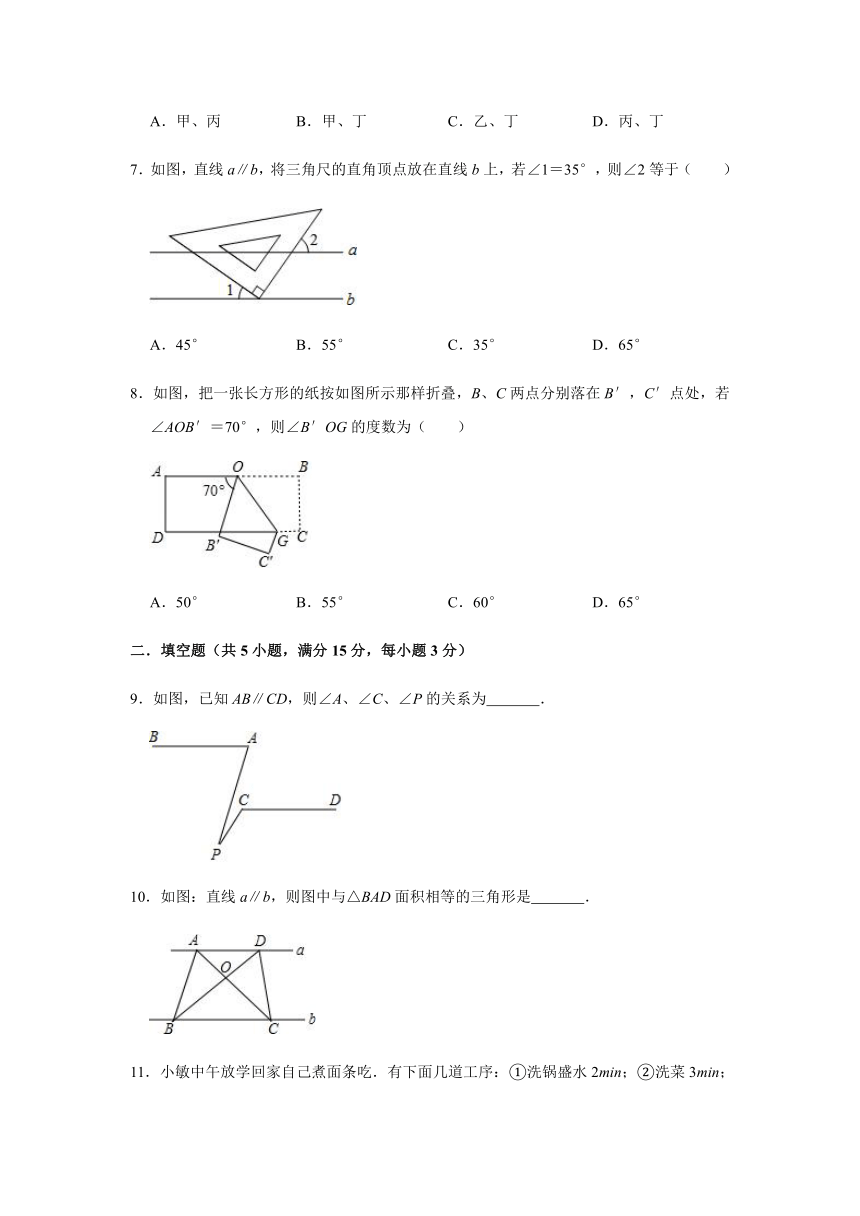
7.如图,直线a∥b,将三角尺的直角顶点放在直线b上,若∠1=35°,则∠2等于( )
A.45°
B.55°
C.35°
D.65°
8.如图,把一张长方形的纸按如图所示那样折叠,B、C两点分别落在B′,C′点处,若∠AOB′=70°,则∠B′OG的度数为( )
A.50°
B.55°
C.60°
D.65°
二.填空题(共5小题,满分15分,每小题3分)
9.如图,已知AB∥CD,则∠A、∠C、∠P的关系为
.
10.如图:直线a∥b,则图中与△BAD面积相等的三角形是
.
11.小敏中午放学回家自己煮面条吃.有下面几道工序:①洗锅盛水2min;②洗菜3min;③准备面条及佐料2min;④用锅把水烧开7min;⑤用烧开的水煮面条和菜要3min.以上各道工序,除④外,一次只能进行一道工序.小敏要将面条煮好,最少需要
min.
12.张老师把红、白、蓝各一个气球分别送给三个小朋友.根据下面三句话,请你猜一猜,他们分到的各是什么颜色的气球?
(1)小春说:“我分到的不是蓝气球.”
(2)小宇说:“我分到的不是白气球.”
(3)小华说:“我看见张老师把蓝气球和红气球分给上面两位小朋友了.”
则小春、小宇、小华分别分到
颜色的气球.
13.如图,AB∥EF,设∠C=90°,那么x,y,z的关系是
.
三.解答题(共7小题,满分52分)
14.(6分)如图,AD∥BC,∠DAC=120°,∠ACF=20°,∠EFC=140°.求证:EF∥AD.
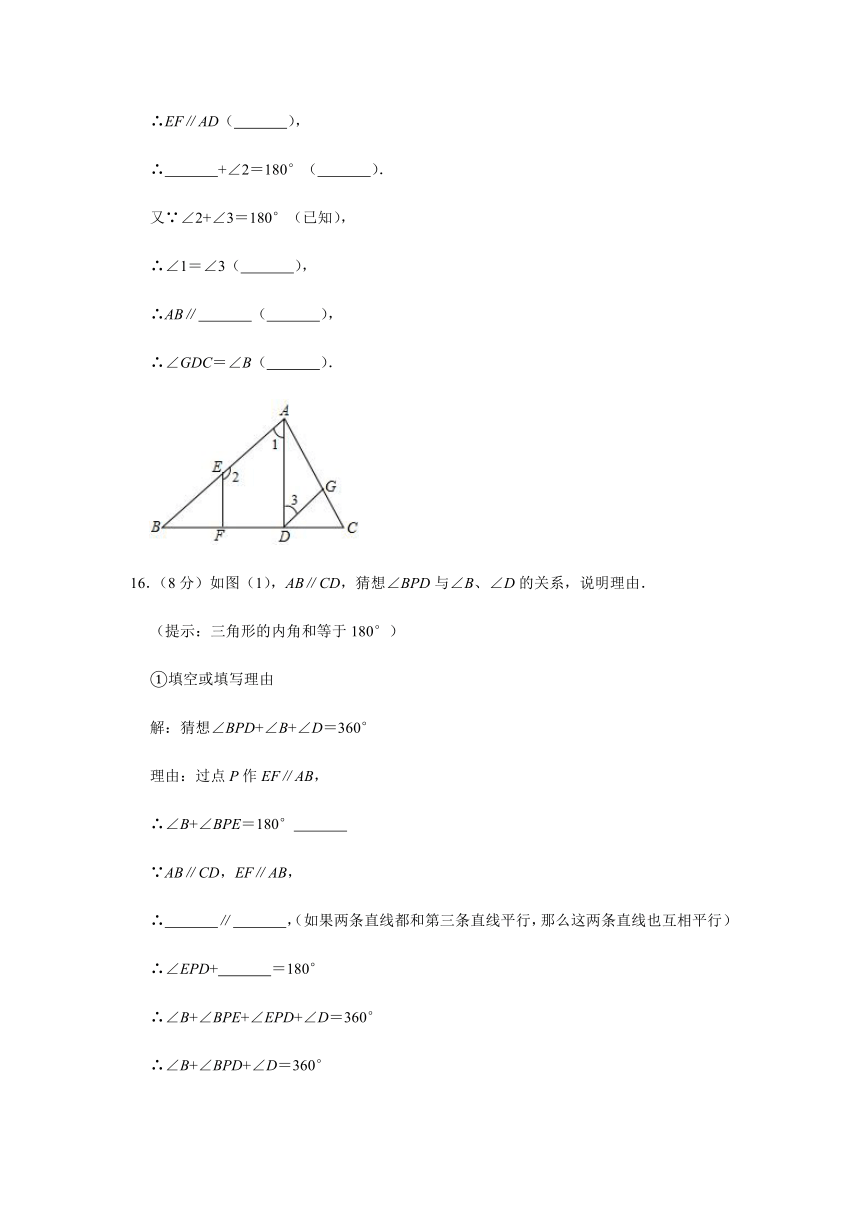
15.(6分)如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90°
,
∴EF∥AD(
),
∴
+∠2=180°(
).
又∵∠2+∠3=180°(已知),
∴∠1=∠3(
),
∴AB∥
(
),
∴∠GDC=∠B(
).
16.(8分)如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说明理由.
(提示:三角形的内角和等于180°)
①填空或填写理由
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°
∵AB∥CD,EF∥AB,
∴
∥
,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+
=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
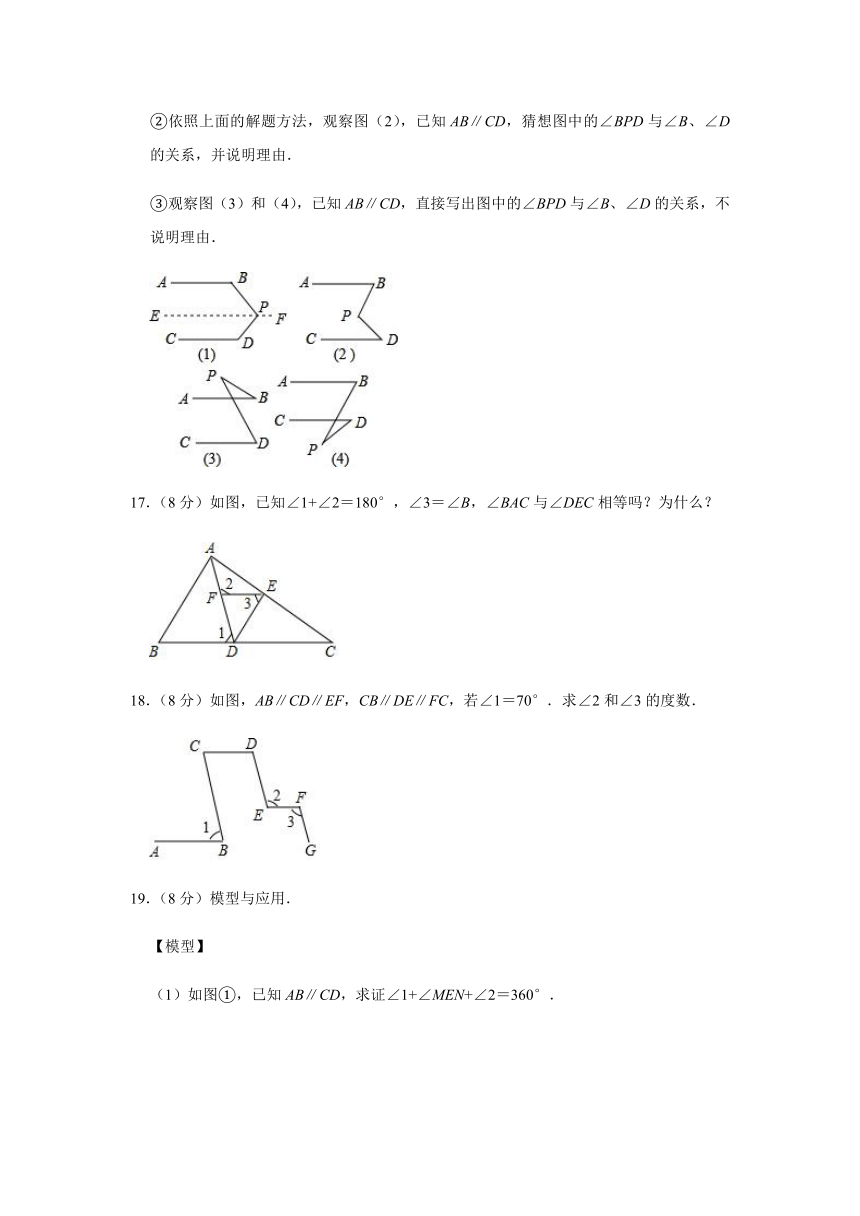
③观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B、∠D的关系,不说明理由.
17.(8分)如图,已知∠1+∠2=180°,∠3=∠B,∠BAC与∠DEC相等吗?为什么?
18.(8分)如图,AB∥CD∥EF,CB∥DE∥FC,若∠1=70°.求∠2和∠3的度数.
19.(8分)模型与应用.
【模型】
(1)如图①,已知AB∥CD,求证∠1+∠MEN+∠2=360°.
【应用】
(2)如图②,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6的度数为
.
如图③,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6+…+∠n的度数为
.
(3)如图④,已知AB∥CD,∠AM1M2的角平分线M1O与∠CMnMn﹣1的角平分线MnO交于点O,若∠M1OMn=m°.在(2)的基础上,求∠2+∠3+∠4+∠5+∠6+……+∠n﹣1的度数.(用含m、n的代数式表示)
20.(8分)(1)如图①,AB∥CD,试问∠2与∠1+∠3的关系是什么?并说明理由;
(2)如图②,AB∥CD,试问∠2+∠4与∠1+∠3+∠5的关系是什么?请直接写出结论;
(3)如图③,AB∥CD,试问∠2+∠4+∠6与∠1+∠3+∠5+∠7的关系是什么?请直接写出结论.
参考答案
一.选择题(共8小题,满分24分,每小题3分)
1.C.
2.
D.
3.
C.
4.
B.
5.
C.
6.
D.
7.
B.
8.
B.
二.填空题(共5小题,满分15分,每小题3分)
9.∠A+∠C﹣∠P=180°.
10.△CAD.
11.
12.
12.红、蓝、白.
13.
x+y﹣z=90°.
三.解答题(共7小题,满分52分)
14.证明:∵AD∥BC,
∴∠DAC+∠ACB=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠BCF=∠ACB﹣∠ACF=40°,
又∵∠EFC=140°,
∴∠BCF+∠EFC=180°,
∴EF∥BC,
∵AD∥BC,
∴EF∥AD.
15.解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90°(垂直的定义),
∴EF∥AD
(同位角相等两直线平行),
∴∠1+∠2=180°(两直线平行同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3
(同角的补角相等),
∴AB∥DG(内错角相等两直线平行),
∴∠GDC=∠B
(两直线平行同位角相等).
故答案为:垂直的定义,同位角相等两直线平行,∠1,两直线平行同旁内角互补,同角的补角相等,DG,内错角相等两直线平行,两直线平行同位角相等.
16.解:①猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴CD∥EF,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+∠CDP=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②猜想∠BPD=∠B+∠D
理由:过点P作EP∥AB,
∴∠B=∠BPE(两直线平行,同位角相等)
∵AB∥CD,EF∥AB,
∴CD∥EF,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD=∠D
∴∠BPD=∠B+∠D
③与②的作法相同,过点P作EP∥AB
(3)∠BPD+∠B=∠D,(4)∠BPD=∠B﹣∠D
17.解:∠BAC=∠DEC,理由如下:
∵∠1+∠2=180°,∠2+∠DFE=180°,
∴∠1=∠DFE,
∴EF∥BC,
∴∠3=∠EDC.
∵∠3=∠B,
∴∠EDC=∠B,
∴AB∥DE,
∴∠BAC=∠DEC.
18.解:∵AB∥CD,∠1=70°,
∴∠C=∠1=70°.
∵CB∥DE,
∴∠D=180°﹣∠C=110°.
∵CD∥EF,
∴∠2=∠D=110°.
∵DE∥FG,
∴∠3=∠2=110°.
19.(1)证明:过点E作EF∥CD,
∵AB∥CD,
∴EF∥AB,
∴∠1+∠MEF=180°,
同理∠2+∠NEF=180°,
∴∠1+∠2+∠MEN=360°;
【应用】
(2)
过E作EQ∥CD,过F作FW∥CD,过G作GR∥CD,过H作HY∥CD,
∵CD∥AB,
∴EQ∥FW∥GR∥HY∥AB∥CD,
∴∠1+∠MEQ=180°,∠QEF+∠EFW=180°,∠WFG+∠FGR=180°,∠RGH+∠GHY=180°,∠YHN+∠6=180°,
∴∠1+∠2+∠3+∠4+∠5+∠6=5×180°=900°,
同理∠1+∠2+∠3+∠4+∠5+∠6+…+∠n=180°(n﹣1),
故答案为:900°,180°(n﹣1);
(3)解:过点O作SR∥AB,
∵AB∥CD,
∴SR∥CD,
∴∠AM1O=∠M1OR
同理∠C
MnO=∠MnOR
∴∠A
M1O+∠CMnO=∠M1OR+∠MnOR,
∴∠A
M1O+∠CMnO=∠M1OMn=m°,
∵M1O平分∠AM1M2,
∴∠AM1M2=2∠A
M1O,
同理∠CMnMn﹣1=2∠CMnO,
∴∠AM1M2+∠CMnMn﹣1=2∠AM1O+2∠CMnO=2∠M1OMn=2m°,
又∵∠A
M1M2+∠2+∠3+∠4+∠5+∠6+……+∠n﹣1+∠CMnMn﹣1=180°(n﹣1),
∠2+∠3+∠4+∠5+∠6+…+∠n﹣1=(180n﹣180﹣2m)°.
20.解:(1)∠2与∠1+∠3的关系是∠2=∠1+∠3,
理由:过点E作EF∥AB,如右图所示,
∵AB∥EF,AB∥CD,
∴AB∥EF∥CD,
∴∠1=∠BEF,∠3=∠CEF,
∴∠2=∠1+∠3;
(2)由(1)可得,
∠2+∠4与∠1+∠3+∠5的关系是∠2+∠4=∠1+∠3+∠5;
(3)由(1)可得,
∠2+∠4+∠6与∠1+∠3+∠5+∠7的关系是∠2+∠4+∠6=∠1+∠3+∠5+∠7.
平行线的性质
一.选择题(共8小题,满分24分,每小题3分)
1.已知直线a∥b,点M到直线a的距离是6cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为( )
A.3
cm
B.9
cm
C.3
cm或9
cm
D.6
cm
2.下列语句是命题的为( )
A.作直线AB的垂线
B.同角的余角相等吗?
C.延长线段AO到C,使OC=OA
D.两直线相交,只有一个交点
3.下列三个命题:①同角的补角相等;②如果b∥a,c∥a,那么b∥c;③如果一个角的两边分别平行于另一个角的两边,那么这两个角相等,其中是真命题的有( )
A.0个
B.1个
C.2个
D.3个
4.说明“如果x<2,那么x2<4”是假命题,可以举一个反例x的值为( )
A.﹣1
B.﹣3
C.0
D.1.5
5.小明中午放学回家自己煮面条吃,有下面几道工序:(1)洗锅盛水2分钟;(2)洗菜3分钟;(3)准备面条及佐料2分钟;(4)用锅把水烧开7分钟;(5)用烧开的水煮面条和菜要3分钟.以上各工序除(4)外,一次只能进行一道工序,小明要将面条煮好,最少用( )
A.14分钟
B.13分钟
C.12分钟
D.11分钟
6.某旅行团在一城市游览,有甲、乙、丙、丁四个景点,导游说:“①要游览甲,就得去乙;②乙、丙只能去一个;③丙、丁要么都去,要么都不去;”根据导游的说法,在下列选项中,该旅行团可能游览的景点是( )
A.甲、丙
B.甲、丁
C.乙、丁
D.丙、丁
7.如图,直线a∥b,将三角尺的直角顶点放在直线b上,若∠1=35°,则∠2等于( )
A.45°
B.55°
C.35°
D.65°
8.如图,把一张长方形的纸按如图所示那样折叠,B、C两点分别落在B′,C′点处,若∠AOB′=70°,则∠B′OG的度数为( )
A.50°
B.55°
C.60°
D.65°
二.填空题(共5小题,满分15分,每小题3分)
9.如图,已知AB∥CD,则∠A、∠C、∠P的关系为
.
10.如图:直线a∥b,则图中与△BAD面积相等的三角形是
.
11.小敏中午放学回家自己煮面条吃.有下面几道工序:①洗锅盛水2min;②洗菜3min;③准备面条及佐料2min;④用锅把水烧开7min;⑤用烧开的水煮面条和菜要3min.以上各道工序,除④外,一次只能进行一道工序.小敏要将面条煮好,最少需要
min.
12.张老师把红、白、蓝各一个气球分别送给三个小朋友.根据下面三句话,请你猜一猜,他们分到的各是什么颜色的气球?
(1)小春说:“我分到的不是蓝气球.”
(2)小宇说:“我分到的不是白气球.”
(3)小华说:“我看见张老师把蓝气球和红气球分给上面两位小朋友了.”
则小春、小宇、小华分别分到
颜色的气球.
13.如图,AB∥EF,设∠C=90°,那么x,y,z的关系是
.
三.解答题(共7小题,满分52分)
14.(6分)如图,AD∥BC,∠DAC=120°,∠ACF=20°,∠EFC=140°.求证:EF∥AD.
15.(6分)如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90°
,
∴EF∥AD(
),
∴
+∠2=180°(
).
又∵∠2+∠3=180°(已知),
∴∠1=∠3(
),
∴AB∥
(
),
∴∠GDC=∠B(
).
16.(8分)如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说明理由.
(提示:三角形的内角和等于180°)
①填空或填写理由
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°
∵AB∥CD,EF∥AB,
∴
∥
,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+
=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
③观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B、∠D的关系,不说明理由.
17.(8分)如图,已知∠1+∠2=180°,∠3=∠B,∠BAC与∠DEC相等吗?为什么?
18.(8分)如图,AB∥CD∥EF,CB∥DE∥FC,若∠1=70°.求∠2和∠3的度数.
19.(8分)模型与应用.
【模型】
(1)如图①,已知AB∥CD,求证∠1+∠MEN+∠2=360°.
【应用】
(2)如图②,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6的度数为
.
如图③,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6+…+∠n的度数为
.
(3)如图④,已知AB∥CD,∠AM1M2的角平分线M1O与∠CMnMn﹣1的角平分线MnO交于点O,若∠M1OMn=m°.在(2)的基础上,求∠2+∠3+∠4+∠5+∠6+……+∠n﹣1的度数.(用含m、n的代数式表示)
20.(8分)(1)如图①,AB∥CD,试问∠2与∠1+∠3的关系是什么?并说明理由;
(2)如图②,AB∥CD,试问∠2+∠4与∠1+∠3+∠5的关系是什么?请直接写出结论;
(3)如图③,AB∥CD,试问∠2+∠4+∠6与∠1+∠3+∠5+∠7的关系是什么?请直接写出结论.
参考答案
一.选择题(共8小题,满分24分,每小题3分)
1.C.
2.
D.
3.
C.
4.
B.
5.
C.
6.
D.
7.
B.
8.
B.
二.填空题(共5小题,满分15分,每小题3分)
9.∠A+∠C﹣∠P=180°.
10.△CAD.
11.
12.
12.红、蓝、白.
13.
x+y﹣z=90°.
三.解答题(共7小题,满分52分)
14.证明:∵AD∥BC,
∴∠DAC+∠ACB=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠BCF=∠ACB﹣∠ACF=40°,
又∵∠EFC=140°,
∴∠BCF+∠EFC=180°,
∴EF∥BC,
∵AD∥BC,
∴EF∥AD.
15.解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90°(垂直的定义),
∴EF∥AD
(同位角相等两直线平行),
∴∠1+∠2=180°(两直线平行同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3
(同角的补角相等),
∴AB∥DG(内错角相等两直线平行),
∴∠GDC=∠B
(两直线平行同位角相等).
故答案为:垂直的定义,同位角相等两直线平行,∠1,两直线平行同旁内角互补,同角的补角相等,DG,内错角相等两直线平行,两直线平行同位角相等.
16.解:①猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴CD∥EF,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD+∠CDP=180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②猜想∠BPD=∠B+∠D
理由:过点P作EP∥AB,
∴∠B=∠BPE(两直线平行,同位角相等)
∵AB∥CD,EF∥AB,
∴CD∥EF,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠EPD=∠D
∴∠BPD=∠B+∠D
③与②的作法相同,过点P作EP∥AB
(3)∠BPD+∠B=∠D,(4)∠BPD=∠B﹣∠D
17.解:∠BAC=∠DEC,理由如下:
∵∠1+∠2=180°,∠2+∠DFE=180°,
∴∠1=∠DFE,
∴EF∥BC,
∴∠3=∠EDC.
∵∠3=∠B,
∴∠EDC=∠B,
∴AB∥DE,
∴∠BAC=∠DEC.
18.解:∵AB∥CD,∠1=70°,
∴∠C=∠1=70°.
∵CB∥DE,
∴∠D=180°﹣∠C=110°.
∵CD∥EF,
∴∠2=∠D=110°.
∵DE∥FG,
∴∠3=∠2=110°.
19.(1)证明:过点E作EF∥CD,
∵AB∥CD,
∴EF∥AB,
∴∠1+∠MEF=180°,
同理∠2+∠NEF=180°,
∴∠1+∠2+∠MEN=360°;
【应用】
(2)
过E作EQ∥CD,过F作FW∥CD,过G作GR∥CD,过H作HY∥CD,
∵CD∥AB,
∴EQ∥FW∥GR∥HY∥AB∥CD,
∴∠1+∠MEQ=180°,∠QEF+∠EFW=180°,∠WFG+∠FGR=180°,∠RGH+∠GHY=180°,∠YHN+∠6=180°,
∴∠1+∠2+∠3+∠4+∠5+∠6=5×180°=900°,
同理∠1+∠2+∠3+∠4+∠5+∠6+…+∠n=180°(n﹣1),
故答案为:900°,180°(n﹣1);
(3)解:过点O作SR∥AB,
∵AB∥CD,
∴SR∥CD,
∴∠AM1O=∠M1OR
同理∠C
MnO=∠MnOR
∴∠A
M1O+∠CMnO=∠M1OR+∠MnOR,
∴∠A
M1O+∠CMnO=∠M1OMn=m°,
∵M1O平分∠AM1M2,
∴∠AM1M2=2∠A
M1O,
同理∠CMnMn﹣1=2∠CMnO,
∴∠AM1M2+∠CMnMn﹣1=2∠AM1O+2∠CMnO=2∠M1OMn=2m°,
又∵∠A
M1M2+∠2+∠3+∠4+∠5+∠6+……+∠n﹣1+∠CMnMn﹣1=180°(n﹣1),
∠2+∠3+∠4+∠5+∠6+…+∠n﹣1=(180n﹣180﹣2m)°.
20.解:(1)∠2与∠1+∠3的关系是∠2=∠1+∠3,
理由:过点E作EF∥AB,如右图所示,
∵AB∥EF,AB∥CD,
∴AB∥EF∥CD,
∴∠1=∠BEF,∠3=∠CEF,
∴∠2=∠1+∠3;
(2)由(1)可得,
∠2+∠4与∠1+∠3+∠5的关系是∠2+∠4=∠1+∠3+∠5;
(3)由(1)可得,
∠2+∠4+∠6与∠1+∠3+∠5+∠7的关系是∠2+∠4+∠6=∠1+∠3+∠5+∠7.
