人教新版七年级数学下册 5.4 平移 同步练习卷(含答案)
文档属性
| 名称 | 人教新版七年级数学下册 5.4 平移 同步练习卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 161.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-07 00:00:00 | ||
图片预览


文档简介
5.4
平移
一.选择题(共10小题)
1.下列几组图形中,通过平移后能够重合的是( )
A.
B.
C.
D.
2.如图是一段台阶的截面示意图(AH≠GH),若要沿A﹣B﹣C﹣D﹣E﹣F﹣G铺上地毯(每个调节的宽度和高度均不同),已知图中所有拐角均为直角.须知地毯的长度,至少需要测量( )
A.2次
B.3次
C.4次
D.6次
3.下列现象中是平移的是( )
A.将一张纸沿它的中线折叠
B.电梯的上下移动
C.飞碟的快速转动
D.翻开书中的每一页纸张
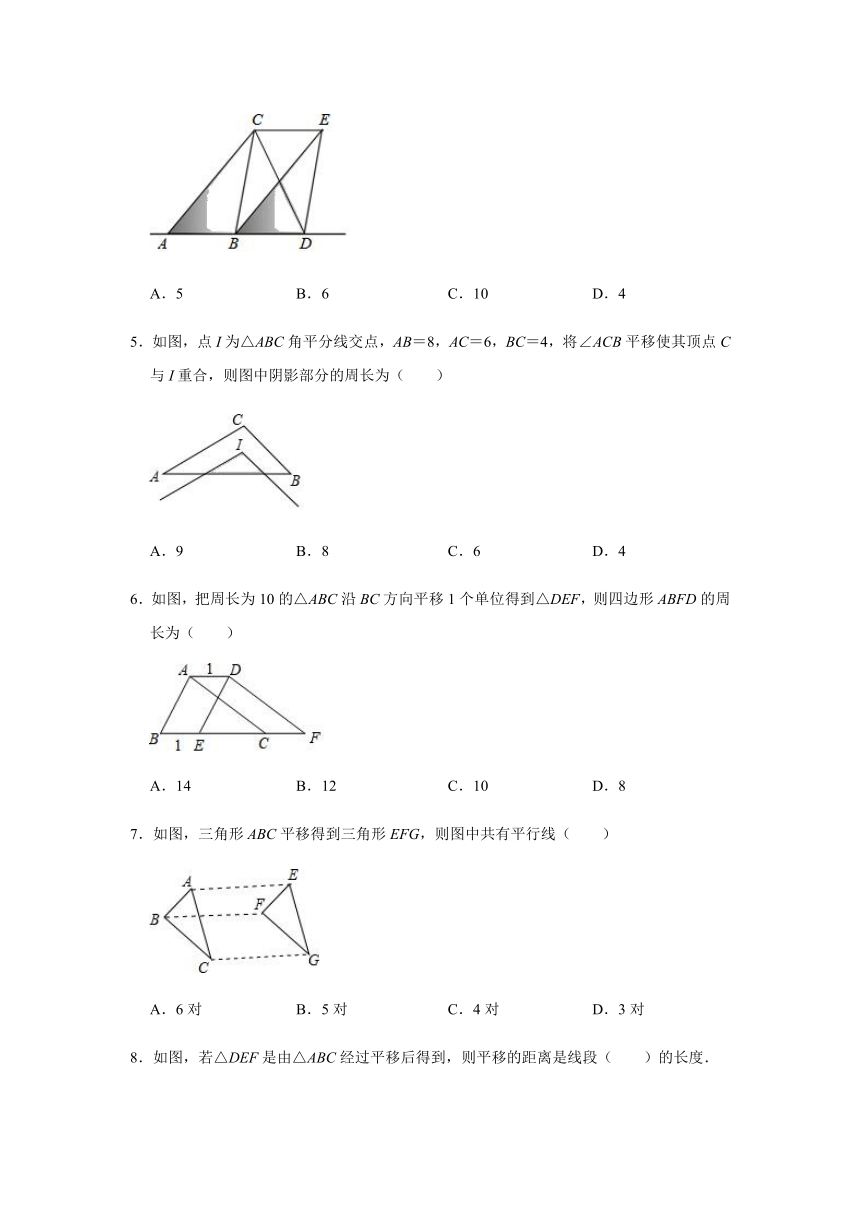
4.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD、CE,若△ACD的面积为10,则△BCE的面积为( )
A.5
B.6
C.10
D.4
5.如图,点I为△ABC角平分线交点,AB=8,AC=6,BC=4,将∠ACB平移使其顶点C与I重合,则图中阴影部分的周长为( )
A.9
B.8
C.6
D.4
6.如图,把周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.14
B.12
C.10
D.8
7.如图,三角形ABC平移得到三角形EFG,则图中共有平行线( )
A.6对
B.5对
C.4对
D.3对
8.如图,若△DEF是由△ABC经过平移后得到,则平移的距离是线段( )的长度.
A.BC
B.EF
C.EC
D.BE
9.如图,两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起,固定三角形ABC不动,将三角形DEF向右平移,当点E和点C重合时,停止移动,设DE交AC于G.给出下列结论:
①四边形ABEG的面积与CGDF的面积相等;
②AD∥EC,且AD=EC,
则( )
A.①,②都正确
B.①正确,②错误
C.①,②都错误
D.①错误,②正确
10.如图三角形ABC平移后得到三角形DEF,若AE=11,DB=5,则平移的距离是( )
A.6
B.3
C.5
D.11
二.填空题(共5小题)
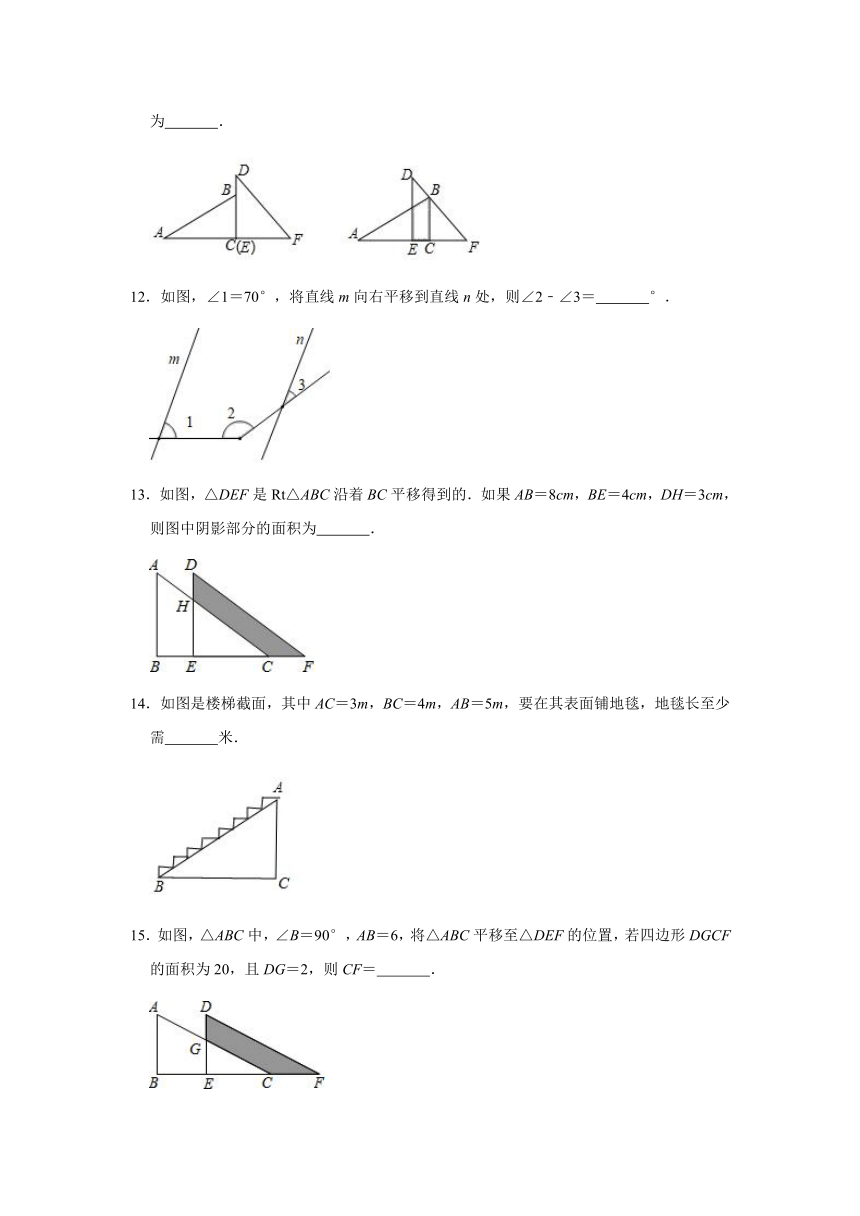
11.已知一副直角三角板如图放置,其中BC=6,EF=8,把30°的三角板向右平移,使顶点B落在45°的三角板的斜边DF上,则两个三角板重叠部分(阴影部分)的面积为
.
12.如图,∠1=70°,将直线m向右平移到直线n处,则∠2﹣∠3=
°.
13.如图,△DEF是Rt△ABC沿着BC平移得到的.如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分的面积为
.
14.如图是楼梯截面,其中AC=3m,BC=4m,AB=5m,要在其表面铺地毯,地毯长至少需
米.
15.如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为20,且DG=2,则CF=
.
三.解答题(共5小题)
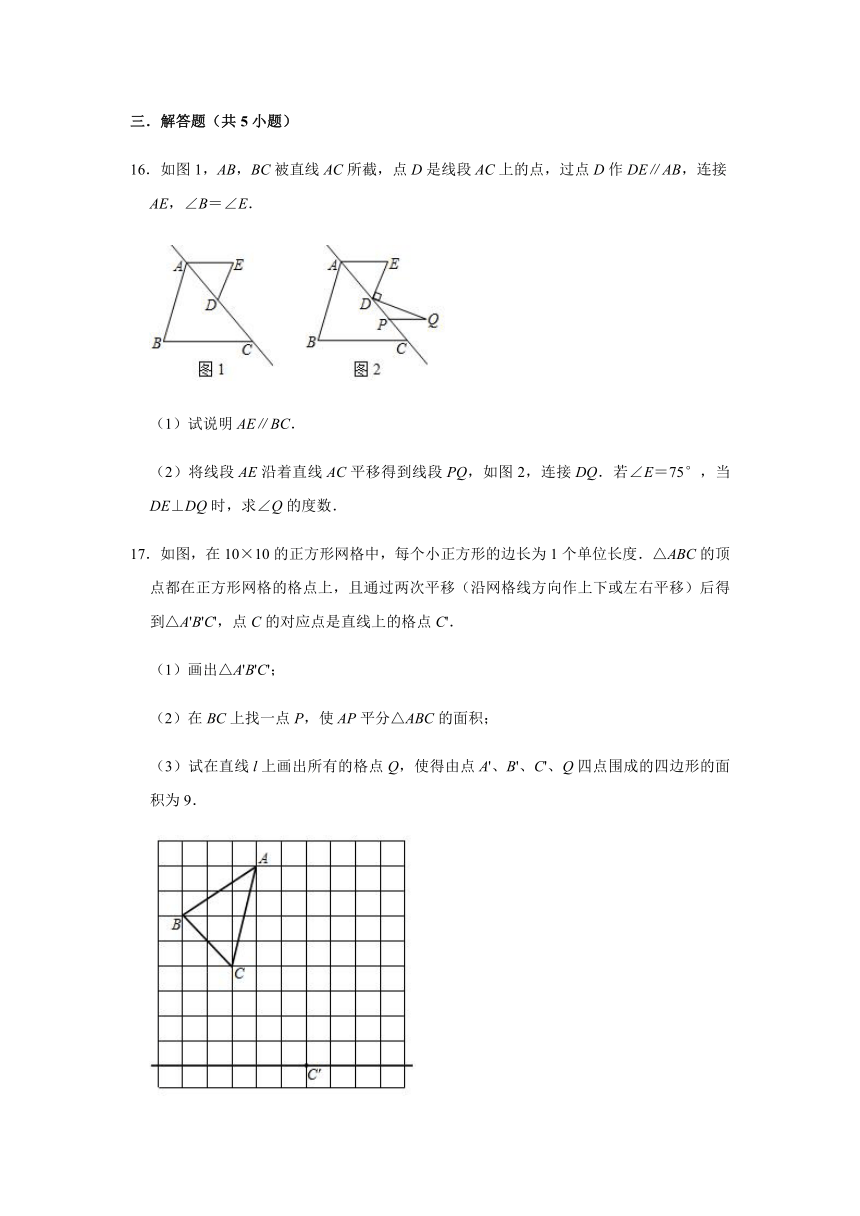
16.如图1,AB,BC被直线AC所截,点D是线段AC上的点,过点D作DE∥AB,连接AE,∠B=∠E.
(1)试说明AE∥BC.
(2)将线段AE沿着直线AC平移得到线段PQ,如图2,连接DQ.若∠E=75°,当DE⊥DQ时,求∠Q的度数.
17.如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A'B'C',点C的对应点是直线上的格点C'.
(1)画出△A'B'C';
(2)在BC上找一点P,使AP平分△ABC的面积;
(3)试在直线l上画出所有的格点Q,使得由点A'、B'、C'、Q四点围成的四边形的面积为9.
18.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
(1)请画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两条线段之间的关系是
.
(3)作直线MN,将△ABC分成两个面积相等的三角形.
19.如图,在方格纸中,每个小正方形的边长均为1个单位长度,有一个△ABC,它的三个顶点均与小正方形的顶点重合.
(1)将△ABC向右平移3个单位长度,得到△DEF(A与D、B与E、C与F对应)请在方格纸中画出△DEF;
(2)在(1)的条件下,连接AE和CE,请求出△ACE的面积S.
20.如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC向左平移5个单位得到△DEF.
(1)在正方形网格中,作出△DEF;
(2)设网格小正方形的边长为1,求平移过程中线段AC所扫过的图形面积.
参考答案
一.选择题(共10小题)
1.
D.
2.
A.
3.
B.
4.
A.
5.
B.
6.
B.
7.
A.
8.
D.
9.
B.
10.
B.
二.填空题(共5小题)
11.
12﹣.
12.
110.
13.
26cm2.
14.
7.
15.
4.
三.解答题(共5小题)
16.解:(1)∵DE∥AB,
∴∠BAE+∠E=180°,
∵∠B=∠E,
∴∠BAE+∠B=180°,
∴AE∥BC;
(2)如图2,过D作DF∥AE交AB于F,
∵PQ∥AE,
∴DF∥PQ,
∵∠E=75°,
∴∠EDF=105°,
∵DE⊥DQ,
∴∠EDQ=90°,
∴∠FDQ=360°﹣105°﹣90°=165°,
∴∠DPQ+∠QDP=165°,
∴∠Q=180°﹣165°=15°.
17.解:(1)如图所示:△A'B'C'即为所求;
(2)如图所示:点P即为所求;
(3)如图所示:点Q即为所求.
18.解:(1)平移后的△A′B′C′如图所示.
(2)根据平移的性质可知,线段AA′,CC′这两条线段之间的关系是相等且平行,
故答案为相等且平行.
(3)构造平行四边形ABCD,对角线BD所在的直线即为所求的直线MN.
19.解:(1)如图所示:
(2)由图可知,
S=5×4﹣×4×1﹣×2×4﹣×2×5=20﹣2﹣4﹣5=9.
20.解:(1)△DEF如图所示.
(2)连接CF,AD.
平移过程中线段AC所扫过的图形面积=平行四边形ADFC的面积=5×3=15.
平移
一.选择题(共10小题)
1.下列几组图形中,通过平移后能够重合的是( )
A.
B.
C.
D.
2.如图是一段台阶的截面示意图(AH≠GH),若要沿A﹣B﹣C﹣D﹣E﹣F﹣G铺上地毯(每个调节的宽度和高度均不同),已知图中所有拐角均为直角.须知地毯的长度,至少需要测量( )
A.2次
B.3次
C.4次
D.6次
3.下列现象中是平移的是( )
A.将一张纸沿它的中线折叠
B.电梯的上下移动
C.飞碟的快速转动
D.翻开书中的每一页纸张
4.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD、CE,若△ACD的面积为10,则△BCE的面积为( )
A.5
B.6
C.10
D.4
5.如图,点I为△ABC角平分线交点,AB=8,AC=6,BC=4,将∠ACB平移使其顶点C与I重合,则图中阴影部分的周长为( )
A.9
B.8
C.6
D.4
6.如图,把周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.14
B.12
C.10
D.8
7.如图,三角形ABC平移得到三角形EFG,则图中共有平行线( )
A.6对
B.5对
C.4对
D.3对
8.如图,若△DEF是由△ABC经过平移后得到,则平移的距离是线段( )的长度.
A.BC
B.EF
C.EC
D.BE
9.如图,两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起,固定三角形ABC不动,将三角形DEF向右平移,当点E和点C重合时,停止移动,设DE交AC于G.给出下列结论:
①四边形ABEG的面积与CGDF的面积相等;
②AD∥EC,且AD=EC,
则( )
A.①,②都正确
B.①正确,②错误
C.①,②都错误
D.①错误,②正确
10.如图三角形ABC平移后得到三角形DEF,若AE=11,DB=5,则平移的距离是( )
A.6
B.3
C.5
D.11
二.填空题(共5小题)
11.已知一副直角三角板如图放置,其中BC=6,EF=8,把30°的三角板向右平移,使顶点B落在45°的三角板的斜边DF上,则两个三角板重叠部分(阴影部分)的面积为
.
12.如图,∠1=70°,将直线m向右平移到直线n处,则∠2﹣∠3=
°.
13.如图,△DEF是Rt△ABC沿着BC平移得到的.如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分的面积为
.
14.如图是楼梯截面,其中AC=3m,BC=4m,AB=5m,要在其表面铺地毯,地毯长至少需
米.
15.如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为20,且DG=2,则CF=
.
三.解答题(共5小题)
16.如图1,AB,BC被直线AC所截,点D是线段AC上的点,过点D作DE∥AB,连接AE,∠B=∠E.
(1)试说明AE∥BC.
(2)将线段AE沿着直线AC平移得到线段PQ,如图2,连接DQ.若∠E=75°,当DE⊥DQ时,求∠Q的度数.
17.如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A'B'C',点C的对应点是直线上的格点C'.
(1)画出△A'B'C';
(2)在BC上找一点P,使AP平分△ABC的面积;
(3)试在直线l上画出所有的格点Q,使得由点A'、B'、C'、Q四点围成的四边形的面积为9.
18.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
(1)请画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两条线段之间的关系是
.
(3)作直线MN,将△ABC分成两个面积相等的三角形.
19.如图,在方格纸中,每个小正方形的边长均为1个单位长度,有一个△ABC,它的三个顶点均与小正方形的顶点重合.
(1)将△ABC向右平移3个单位长度,得到△DEF(A与D、B与E、C与F对应)请在方格纸中画出△DEF;
(2)在(1)的条件下,连接AE和CE,请求出△ACE的面积S.
20.如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC向左平移5个单位得到△DEF.
(1)在正方形网格中,作出△DEF;
(2)设网格小正方形的边长为1,求平移过程中线段AC所扫过的图形面积.
参考答案
一.选择题(共10小题)
1.
D.
2.
A.
3.
B.
4.
A.
5.
B.
6.
B.
7.
A.
8.
D.
9.
B.
10.
B.
二.填空题(共5小题)
11.
12﹣.
12.
110.
13.
26cm2.
14.
7.
15.
4.
三.解答题(共5小题)
16.解:(1)∵DE∥AB,
∴∠BAE+∠E=180°,
∵∠B=∠E,
∴∠BAE+∠B=180°,
∴AE∥BC;
(2)如图2,过D作DF∥AE交AB于F,
∵PQ∥AE,
∴DF∥PQ,
∵∠E=75°,
∴∠EDF=105°,
∵DE⊥DQ,
∴∠EDQ=90°,
∴∠FDQ=360°﹣105°﹣90°=165°,
∴∠DPQ+∠QDP=165°,
∴∠Q=180°﹣165°=15°.
17.解:(1)如图所示:△A'B'C'即为所求;
(2)如图所示:点P即为所求;
(3)如图所示:点Q即为所求.
18.解:(1)平移后的△A′B′C′如图所示.
(2)根据平移的性质可知,线段AA′,CC′这两条线段之间的关系是相等且平行,
故答案为相等且平行.
(3)构造平行四边形ABCD,对角线BD所在的直线即为所求的直线MN.
19.解:(1)如图所示:
(2)由图可知,
S=5×4﹣×4×1﹣×2×4﹣×2×5=20﹣2﹣4﹣5=9.
20.解:(1)△DEF如图所示.
(2)连接CF,AD.
平移过程中线段AC所扫过的图形面积=平行四边形ADFC的面积=5×3=15.
