北师大版八年级下册5.4分式方程专题练习题含答案
文档属性
| 名称 | 北师大版八年级下册5.4分式方程专题练习题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 369.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 10:42:23 | ||
图片预览


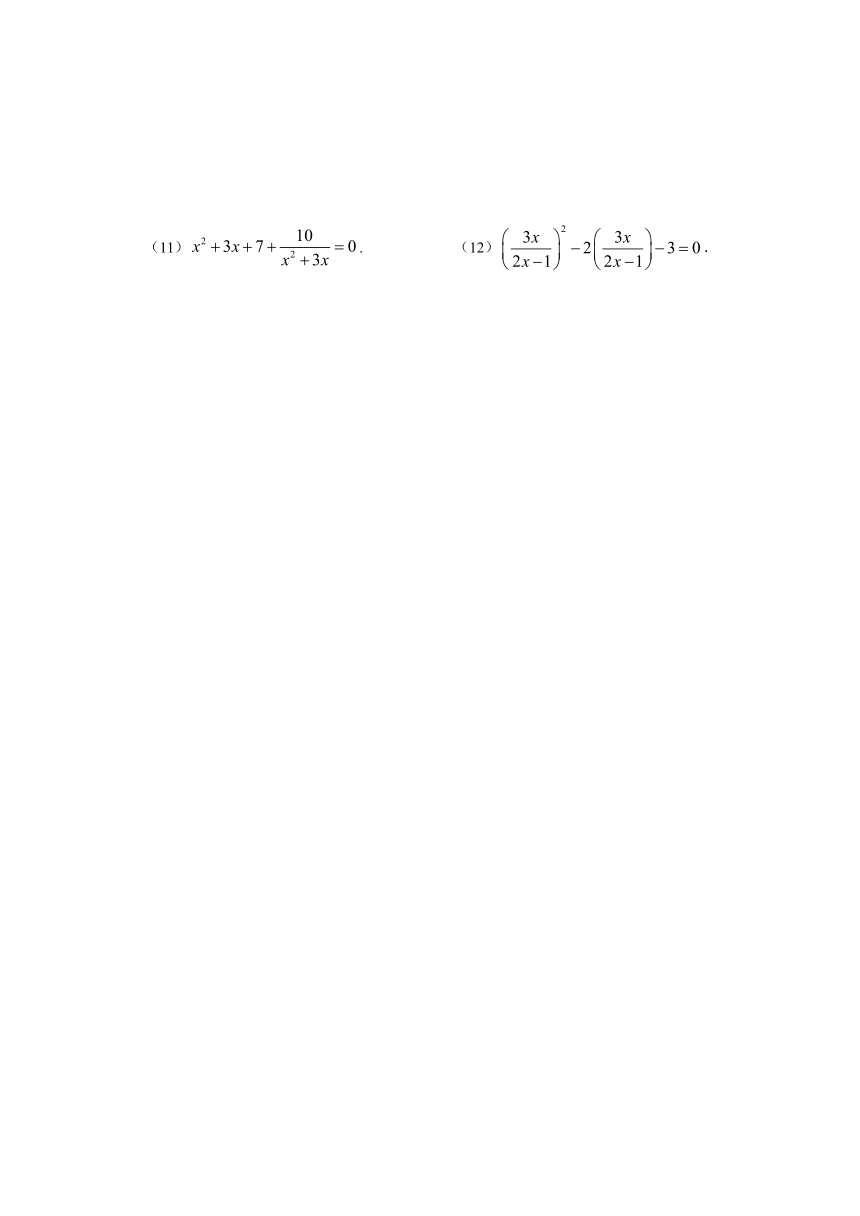
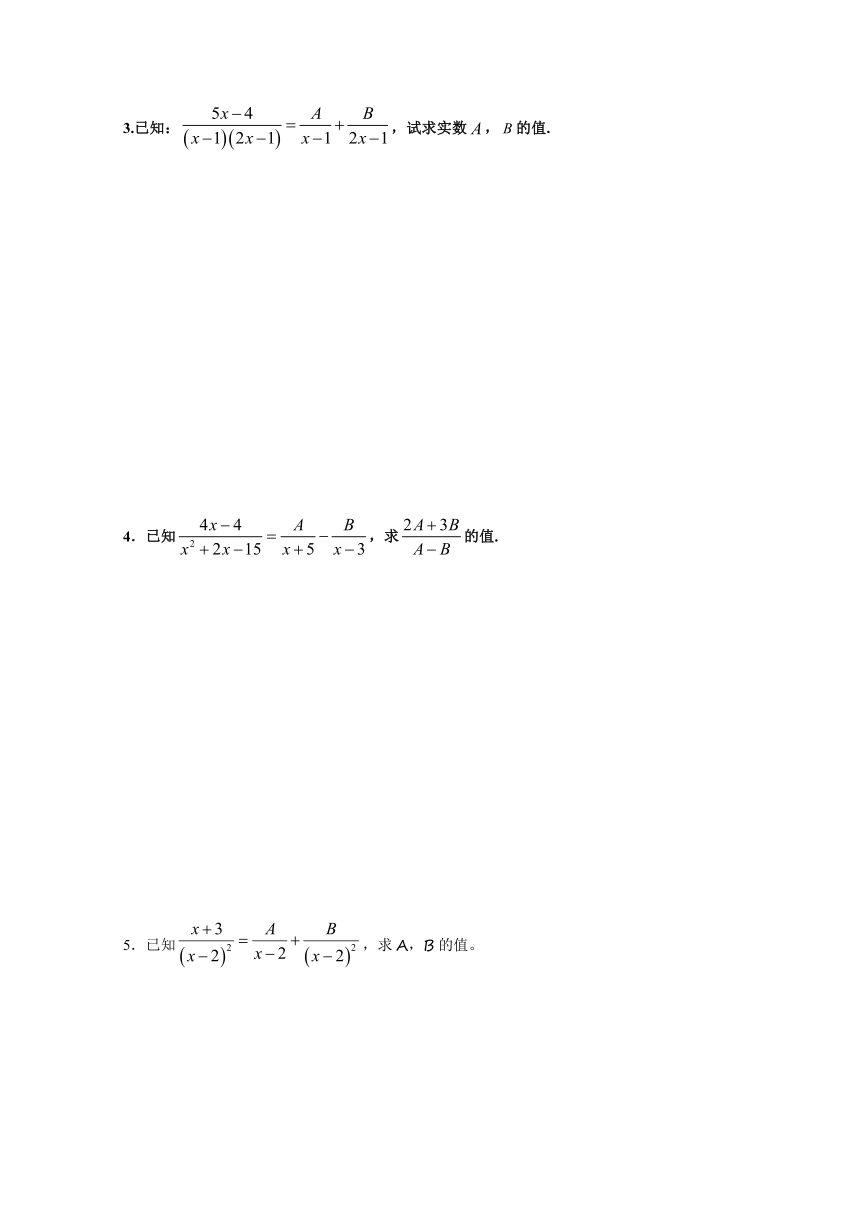

文档简介
第五章分式与分式方程
第四节分式方程
1.在下列方程:①、②、③、④、⑤⑥,⑦,⑧,⑨中,那些是分式方程,并说明理由。
2.解下列分式方程
(1)
;
(2)
;
(3)
;
(4)
.
(5).
(6).
(7).
(8)
(9)
(10)
(11).
(12).
3.已知:,试求实数,的值.
4.已知,求的值.
5.已知,求A,B的值。
6.已知关于x的方程无解,求m的值.
7.某单位在疫情期间用
3000
元购进
A、B
两种口罩1100
个,购买A种口罩与购买
B
种口罩的费用相同,且A种口罩的单价是
B
种口罩单价的
1.2
倍求
A,B
两种口罩的单价各是多少元?
8.某书店老板去图书批发市场购买某种图书,第一次用500元购书若干本,很快售完由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用900元所购该书的数量比第一次的数量多了10本.
(1)求第一次购书每本多少元?
(2)如果这两次所购图书的售价相同,且全部售完后总利润不低于25%,那么每本图书的售价至少是多少元?
9.某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少;
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种,并确定获利最大的方案以及最大利润;
(3)实际进货时,厂家对电冰箱出厂价下调k(0<k<100)元,若商店保持这两种家电的售价不变,请你根据以上信息及(2)问中条件,设计出使这100台家电销售总利润最大的进货方案.
10.某厂原计划在规定时间内生产通讯设备60台,由于改进了操作技术,每天生产的台数比原计划多50%,结果提前两天完成任务.求改进操作技术后每天生产通讯设备多少台.
11.甲、乙两个服装厂加工同种型号的防护服,甲厂每天加工的数量是乙厂每天加工数量的1.5倍,两厂各加工600套防护服,甲厂比乙厂要少用4天.
(1)求甲、乙两厂每天各加工多少套防护服?
(2)已知甲、乙两厂加工这种防护服每天的费用分别是150元和120元,疫情期间,某医院紧急需要3000套这种防护服,甲厂单独加工一段时间后另有安排,剩下任务只能由乙单独完成.如果总加工费不超过6360元,那么甲厂至少要加工多少天?
12.一列火车从车站开出,预计行程为450千米,当它出发3小时后,因特殊情况而多
停一站,因此耽误30分钟,后来把速度提高了20%,结果准时到达目的地,求这列火车原来的速度。
13.小明的家离学校1600米,一天小明从家出发去上学,出发10分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,正好在校门口追上他,已知爸爸的速度是小明速度的2倍,求小明的速度.
第五章分式与分式方程
第四节分式方程
1.解:方程①②⑥⑧分母中不含未知数,故①②不是分式方程;
方程③④⑤⑦分母中含表示未知数的字母,故是分式方程;
方程⑨属于无理方程。
2.(1)
x=2.(2)
x=3.(3)
x=-2.
(4)无解.
(5)解:
,
,,
检验:当时,,所以是原方程的增根,原方程无解.
(6)去分母得:15x﹣12=4x+10﹣3x+6,移项合并得:14x=28,解得:x=2,
经检验x=2是增根,分式方程无解.
(7)解:,方程两边乘得:,
解得:,检验:当时,.所以原方程的解为.
(8)去分母得:﹣3(x+2)=3(x+2)﹣6+x,去括号得:﹣3x﹣6=3x+6﹣6+x,
移项合并得:7x=﹣6,解得:x=﹣,经检验x=﹣是分式方程的解.
(9)去分母得:
去括号得:
移项合并得:解得:
x=0.经检验x=0,是方程的解.
(10)解:-1=,去分母,得:,
整理,得:x2+3x-4=0,解得:x1=-4,x2=1.经检验:x2=1是增根,舍去,
∴原方程的解是.
(11)解:设,则原方程可化为,解得,或.
当时,,解得,.当时,,方程无解.
经检验,都是原方程的根,∴原方程的根是,.
(12)设,则原方程变形为y2-2y-3=0.解这个方程,得y1=-1,y2=3,
∴或.解得x=或x=1.
经检验:x=或x=1都是原方程的解.
∴原方程的解是x=或x=1.
3.【答案】4.【答案】;5.A=1,B=5;6.-3或1
7.设B
种口罩单价为x元,则A种口罩单价为1.2x元,根据题意列方程得
,解得,经检验,x=2.5是原分式方程的解,∴1.2x=3,
答:
A种口罩单价为3元,B种口罩单价为2.5元.
8.(1)设第一次购书的进价是x元/本,则第二批每套的进价是(1+20%)x元/本,
根据题意得:=-10,解得:x=25,
经检验,x=25是原分式方程的解.答:第一次购书每本25元.
(2)设每本图书的售价为y元,
根据题意得:[500÷25+(500÷25+10)]y-500-900≥(500+900)×25%,
解得:y≥35.答:每本图书的售价至少是35元.
9.解:(1)设每台空调的进价为x元,则每台电冰箱的进价为(x+400)元,根据题意得:
,解得:x=1600,
经检验,x=1600是原方程的解,x+400=1600+400=2000,
答:每台空调的进价为1600元,则每台电冰箱的进价为2000元.
(2)设购进电冰箱x台,这100台家电的销售总利润为y元,
则y=(2100﹣2000)x+(1750﹣1600)(100﹣x)=﹣50x+15000,根据题意得:
,解得:,
∵x为正整数,∴x=34,35,36,37,38,39,40,
∴合理的方案共有7种,即①电冰箱34台,空调66台;②电冰箱35台,空调65台;③电冰箱36台,空调64台;④电冰箱37台,空调63台;⑤电冰箱38台,空调62台;⑥电冰箱39台,空调61台;⑦电冰箱40台,空调60台;
∵y=﹣50x+15000,k=﹣50<0,∴y随x的增大而减小,
∴当x=34时,y有最大值,最大值为:﹣50×34+15000=13300(元),
答:当购进电冰箱34台,空调66台获利最大,最大利润为13300元.
(3)当厂家对电冰箱出厂价下调k(0<k<100)元,若商店保持这两种家电的售价不变,
则利润y=(2100﹣2000+k)x+(1750﹣1600)(100﹣x)=(k﹣50)x+15000,
当k﹣50>0,即50<k<100时,y随x的增大而增大,
∵,
∴当x=40时,这100台家电销售总利润最大,即购进电冰箱40台,空调60台;
当k﹣50<0,即0<k<50时,y随x的增大而减小,
∵,
∴当x=34时,这100台家电销售总利润最大,即购进电冰箱34台,空调66台;
答:当50<k<100时,购进电冰箱40台,空调60台销售总利润最大;当0<k<50时,购进电冰箱34台,空调66台销售总利润最大.
10.解:设改进技术前每天生产x台,根据题意,得,解得x=10,经检验知x=10是原方程的解,则1.5x=15.所以改进操作技术后每天生产通讯设备15台.
11.解:(1)设乙厂每天加工x套防护服,则甲每天加工1.5x套,由题意得:
解之得:x=50,经检验,x=50是原方程的解.
故答案为:乙厂每天加工50套防护服,甲厂每天加工75套防护服.
(2)设甲至少加工a天,乙厂加工了b天,由题意得:
由式得:,代入中,
∴解之得:,当时,符合问题的实际意义,故甲至少要加工28天.故答案为:甲至少要加工28天.
12.解:设这列火车原来的速度为x千米/时,根据题意,得=3++.解得x=75.经检验知x=75是原方程的解.所以,这列火车原来的速度为75千米/时.
13.小明的速度为80米/分.
设小明的速度是x米/分,爸爸的速度是2x米/分,由题意得
解得x=80,
经检验,x=80是方程的根,所以小明的速度是80米/分.
第四节分式方程
1.在下列方程:①、②、③、④、⑤⑥,⑦,⑧,⑨中,那些是分式方程,并说明理由。
2.解下列分式方程
(1)
;
(2)
;
(3)
;
(4)
.
(5).
(6).
(7).
(8)
(9)
(10)
(11).
(12).
3.已知:,试求实数,的值.
4.已知,求的值.
5.已知,求A,B的值。
6.已知关于x的方程无解,求m的值.
7.某单位在疫情期间用
3000
元购进
A、B
两种口罩1100
个,购买A种口罩与购买
B
种口罩的费用相同,且A种口罩的单价是
B
种口罩单价的
1.2
倍求
A,B
两种口罩的单价各是多少元?
8.某书店老板去图书批发市场购买某种图书,第一次用500元购书若干本,很快售完由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用900元所购该书的数量比第一次的数量多了10本.
(1)求第一次购书每本多少元?
(2)如果这两次所购图书的售价相同,且全部售完后总利润不低于25%,那么每本图书的售价至少是多少元?
9.某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少;
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种,并确定获利最大的方案以及最大利润;
(3)实际进货时,厂家对电冰箱出厂价下调k(0<k<100)元,若商店保持这两种家电的售价不变,请你根据以上信息及(2)问中条件,设计出使这100台家电销售总利润最大的进货方案.
10.某厂原计划在规定时间内生产通讯设备60台,由于改进了操作技术,每天生产的台数比原计划多50%,结果提前两天完成任务.求改进操作技术后每天生产通讯设备多少台.
11.甲、乙两个服装厂加工同种型号的防护服,甲厂每天加工的数量是乙厂每天加工数量的1.5倍,两厂各加工600套防护服,甲厂比乙厂要少用4天.
(1)求甲、乙两厂每天各加工多少套防护服?
(2)已知甲、乙两厂加工这种防护服每天的费用分别是150元和120元,疫情期间,某医院紧急需要3000套这种防护服,甲厂单独加工一段时间后另有安排,剩下任务只能由乙单独完成.如果总加工费不超过6360元,那么甲厂至少要加工多少天?
12.一列火车从车站开出,预计行程为450千米,当它出发3小时后,因特殊情况而多
停一站,因此耽误30分钟,后来把速度提高了20%,结果准时到达目的地,求这列火车原来的速度。
13.小明的家离学校1600米,一天小明从家出发去上学,出发10分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,正好在校门口追上他,已知爸爸的速度是小明速度的2倍,求小明的速度.
第五章分式与分式方程
第四节分式方程
1.解:方程①②⑥⑧分母中不含未知数,故①②不是分式方程;
方程③④⑤⑦分母中含表示未知数的字母,故是分式方程;
方程⑨属于无理方程。
2.(1)
x=2.(2)
x=3.(3)
x=-2.
(4)无解.
(5)解:
,
,,
检验:当时,,所以是原方程的增根,原方程无解.
(6)去分母得:15x﹣12=4x+10﹣3x+6,移项合并得:14x=28,解得:x=2,
经检验x=2是增根,分式方程无解.
(7)解:,方程两边乘得:,
解得:,检验:当时,.所以原方程的解为.
(8)去分母得:﹣3(x+2)=3(x+2)﹣6+x,去括号得:﹣3x﹣6=3x+6﹣6+x,
移项合并得:7x=﹣6,解得:x=﹣,经检验x=﹣是分式方程的解.
(9)去分母得:
去括号得:
移项合并得:解得:
x=0.经检验x=0,是方程的解.
(10)解:-1=,去分母,得:,
整理,得:x2+3x-4=0,解得:x1=-4,x2=1.经检验:x2=1是增根,舍去,
∴原方程的解是.
(11)解:设,则原方程可化为,解得,或.
当时,,解得,.当时,,方程无解.
经检验,都是原方程的根,∴原方程的根是,.
(12)设,则原方程变形为y2-2y-3=0.解这个方程,得y1=-1,y2=3,
∴或.解得x=或x=1.
经检验:x=或x=1都是原方程的解.
∴原方程的解是x=或x=1.
3.【答案】4.【答案】;5.A=1,B=5;6.-3或1
7.设B
种口罩单价为x元,则A种口罩单价为1.2x元,根据题意列方程得
,解得,经检验,x=2.5是原分式方程的解,∴1.2x=3,
答:
A种口罩单价为3元,B种口罩单价为2.5元.
8.(1)设第一次购书的进价是x元/本,则第二批每套的进价是(1+20%)x元/本,
根据题意得:=-10,解得:x=25,
经检验,x=25是原分式方程的解.答:第一次购书每本25元.
(2)设每本图书的售价为y元,
根据题意得:[500÷25+(500÷25+10)]y-500-900≥(500+900)×25%,
解得:y≥35.答:每本图书的售价至少是35元.
9.解:(1)设每台空调的进价为x元,则每台电冰箱的进价为(x+400)元,根据题意得:
,解得:x=1600,
经检验,x=1600是原方程的解,x+400=1600+400=2000,
答:每台空调的进价为1600元,则每台电冰箱的进价为2000元.
(2)设购进电冰箱x台,这100台家电的销售总利润为y元,
则y=(2100﹣2000)x+(1750﹣1600)(100﹣x)=﹣50x+15000,根据题意得:
,解得:,
∵x为正整数,∴x=34,35,36,37,38,39,40,
∴合理的方案共有7种,即①电冰箱34台,空调66台;②电冰箱35台,空调65台;③电冰箱36台,空调64台;④电冰箱37台,空调63台;⑤电冰箱38台,空调62台;⑥电冰箱39台,空调61台;⑦电冰箱40台,空调60台;
∵y=﹣50x+15000,k=﹣50<0,∴y随x的增大而减小,
∴当x=34时,y有最大值,最大值为:﹣50×34+15000=13300(元),
答:当购进电冰箱34台,空调66台获利最大,最大利润为13300元.
(3)当厂家对电冰箱出厂价下调k(0<k<100)元,若商店保持这两种家电的售价不变,
则利润y=(2100﹣2000+k)x+(1750﹣1600)(100﹣x)=(k﹣50)x+15000,
当k﹣50>0,即50<k<100时,y随x的增大而增大,
∵,
∴当x=40时,这100台家电销售总利润最大,即购进电冰箱40台,空调60台;
当k﹣50<0,即0<k<50时,y随x的增大而减小,
∵,
∴当x=34时,这100台家电销售总利润最大,即购进电冰箱34台,空调66台;
答:当50<k<100时,购进电冰箱40台,空调60台销售总利润最大;当0<k<50时,购进电冰箱34台,空调66台销售总利润最大.
10.解:设改进技术前每天生产x台,根据题意,得,解得x=10,经检验知x=10是原方程的解,则1.5x=15.所以改进操作技术后每天生产通讯设备15台.
11.解:(1)设乙厂每天加工x套防护服,则甲每天加工1.5x套,由题意得:
解之得:x=50,经检验,x=50是原方程的解.
故答案为:乙厂每天加工50套防护服,甲厂每天加工75套防护服.
(2)设甲至少加工a天,乙厂加工了b天,由题意得:
由式得:,代入中,
∴解之得:,当时,符合问题的实际意义,故甲至少要加工28天.故答案为:甲至少要加工28天.
12.解:设这列火车原来的速度为x千米/时,根据题意,得=3++.解得x=75.经检验知x=75是原方程的解.所以,这列火车原来的速度为75千米/时.
13.小明的速度为80米/分.
设小明的速度是x米/分,爸爸的速度是2x米/分,由题意得
解得x=80,
经检验,x=80是方程的根,所以小明的速度是80米/分.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
