冀教版七年级下册数学:8.5 平方差公式课件 (共25张PPT)
文档属性
| 名称 | 冀教版七年级下册数学:8.5 平方差公式课件 (共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 14:01:22 | ||
图片预览



文档简介
(共25张PPT)
8.5
乘法公式
---平方差公式
1.推导并理解平方差公式
2.会运用平方差公式进行相关计算
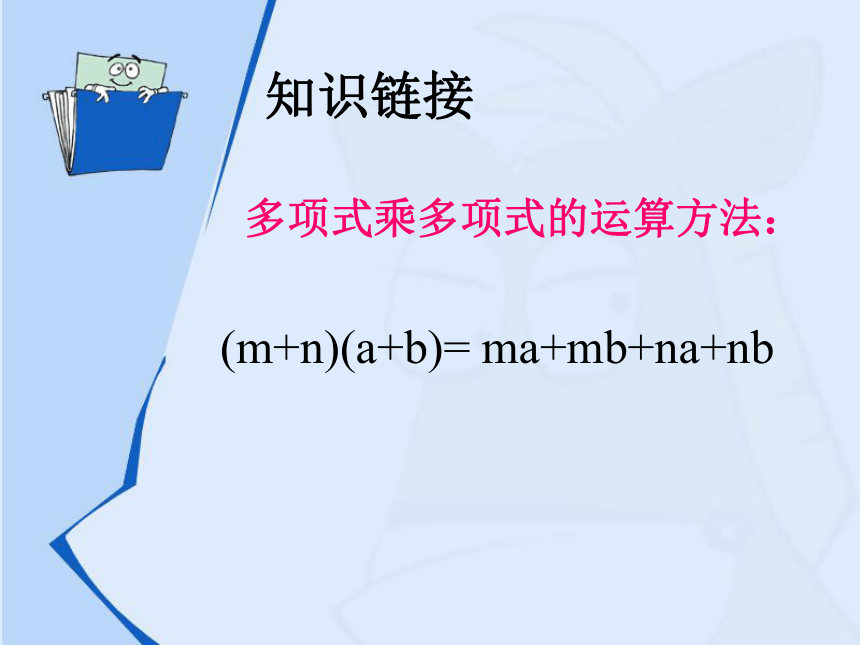
学习目标:
知识链接
多项式乘多项式的运算方法:
(m+n)(a+b)=
ma+mb+na+nb
你能运用多项式乘以多项式的法则进行运算
(1)
=
(2)
=
(3)
=
一练
八分钟
左边=
=右边
1.代数验证:
你能用整式的乘法验证公式的
正确性吗?
(多项式乘以多项式的法则)
(合并同类项法则)
a2-b2
(a+b)(a-b)
(a+b)(a-b)=a2-b2
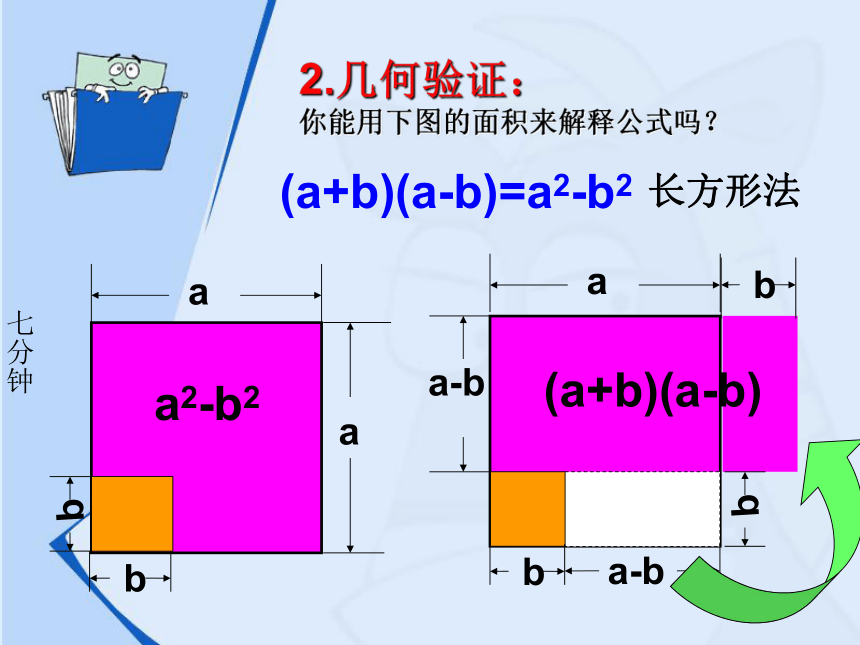
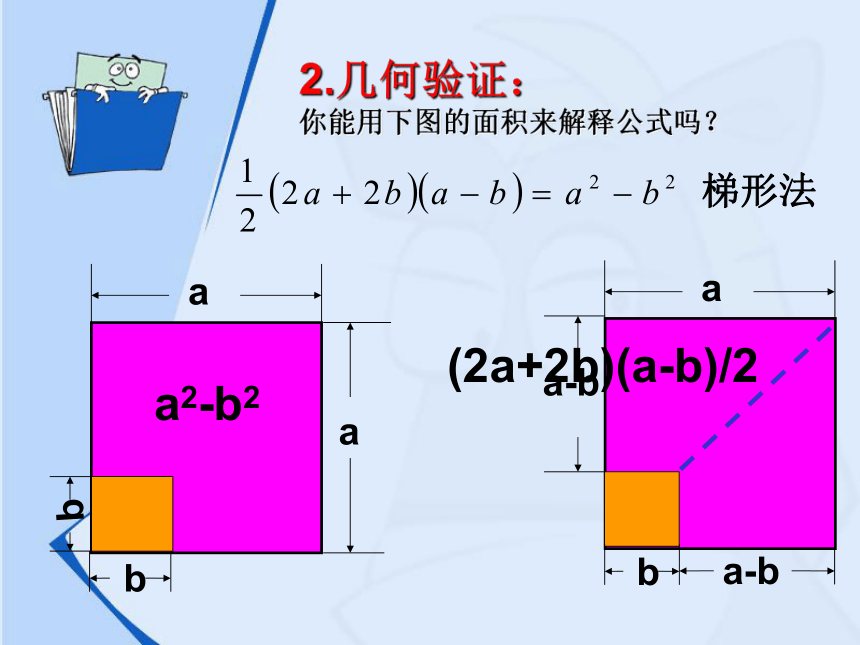
2.几何验证:
你能用下图的面积来解释公式吗?
七分钟
长方形法
a2-b2
(2a+2b)(a-b)/2
2.几何验证:
你能用下图的面积来解释公式吗?
梯形法
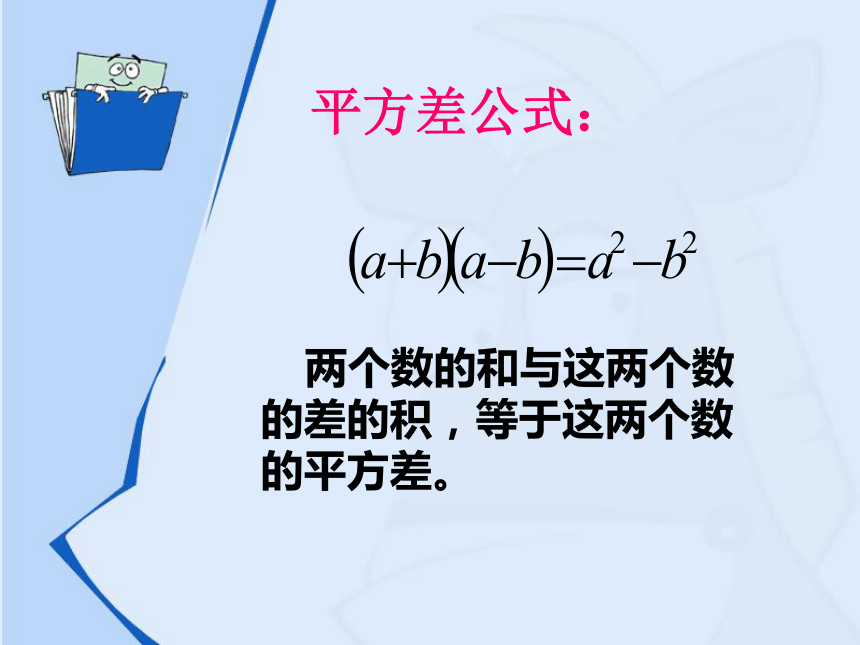
平方差公式:
两个数的和与这两个数的差的积,等于这两个数的平方差。
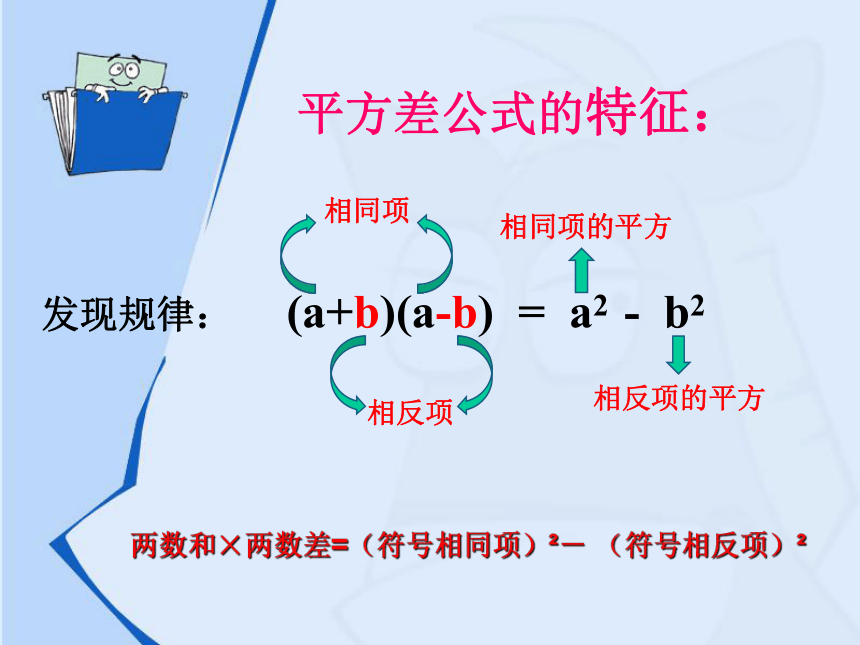
发现规律:
(a+b)(a-b)
=
a2
-
b2
相同项
相反项
相同项的平方
相反项的平方
平方差公式的特征:
两数和×两数差=(符号相同项)?-
(符号相反项)?
(a+b)(a-b)=a2-b2
公式中的a,b可以表示一个单项式也可以表示一个多项式.
注意事项:
您能从下列式子里找出平方差公式中的
“朋友a”和“朋友b”吗?
(1)(2x-3)(2x+3)
(2)(-2x+3)(-2x-3)
(3)(3-2x)(-2x-3)
(4)(2y-x)(-2y-x)
(5)(-x+2y)(-x-2y)
(6)(-3x+2)(3x+2)
a=2x
b=3
a=-2x
b=3
a=-2x
b=3
a=-x
b=2y
a=-x
b=2y
a=2
b=3x
练习:当堂训练1
二练
十分钟
(不能)
1.下列各式中,能用平方差公式运算
的是(
)
A.(-a+b)(-a-b)
B.(a-b)(b-a)
C.(2a-3b)(3a+2b)
D.(a-b+c)(b-a-c)
2.下列多项式相乘,不能用平方差公式
计算的是(
)
A.(x-2y)(2y+x)
B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y)
D.(-2b-5)(2b-5)
A
C
练习:当堂训练1
二练
二分钟
例
用平方差公式计算:102×98
102
×98
=
(100+2)
(100-2)
=
1002-22
=
10000-4
=
9996
解:
×
二分钟
498
×502
=
(500-2)
(500+2)
=
5002-22
=
250000-4
=
249996
解:
×
练习:当堂训练2
利用平方差公式计算:
498×502
三分钟
例
利用平方差公式计算:
解:
三分钟
计算:
1、(2+1)(22+1)(24+1)(28+1)+1
练习:当堂训练3
运用平方差公式计算:
1、(m+n)(-n+m)
=
2、(-x-y)
(-x+y)
=
3、(2a+b)(2a-b)
=
4、(x2+y2)(x2-y2)=
5、
99
×
101
=
m2-n2
x2-y2
4a2-b2
x4-y4
1002-12=9999
(a+b)(a-b)=a2-b2
课堂小结
通过本节课的学习,你收获了什么?
课后练习
课本P88
课内练习1、2
习题A组1、2
1.什么是平方差公式?
2.运用公式要注意什么?
小结
4.计算:
(1)
(3x+2)(3x-2)=
(2)
(b+2a)(2a-b)=
(3)
(-x+2y)(-x-2y)=
9x2-4
4a2-b2
x2-4y2
练习:当堂训练
练习:当堂训练3
计算
20042
-
2003×2005
解:
20042
-
2003×2005
=
20042
-(2004-1)×(2004+1)
=
20042
-
(20042-12
)
=
20042
-
20042+12
—去括号变号
=1
运用新知
例1、(1)(4m+3)(1-2c)
(2)
(-x+3y)(-x-3y)
哪个是
a
哪个是
b
x?-9y?
解:
(a
+b)
(a-b)
=
1?-(2c)?
=
(1)(1+2c)(1-2c)
=
(2)(-x+3y)(-x-3y)=
(-x)?–(3y)?=
(a
+
b)
(
a
-
b)
=
1-4c?
a?-
b?
a?
-
b?
两数和×两数差=(符号相同项)?-
(符号相反项)?
二分钟
一练
(不能)
(能)
(能)
(不能)
3.下列各式能否用平方差公式
进行计算?
⑶
练习:当堂训练2
P88习题A组2(2)(4)、3、4(2)
作业
8.5
乘法公式
---平方差公式
1.推导并理解平方差公式
2.会运用平方差公式进行相关计算
学习目标:
知识链接
多项式乘多项式的运算方法:
(m+n)(a+b)=
ma+mb+na+nb
你能运用多项式乘以多项式的法则进行运算
(1)
=
(2)
=
(3)
=
一练
八分钟
左边=
=右边
1.代数验证:
你能用整式的乘法验证公式的
正确性吗?
(多项式乘以多项式的法则)
(合并同类项法则)
a2-b2
(a+b)(a-b)
(a+b)(a-b)=a2-b2
2.几何验证:
你能用下图的面积来解释公式吗?
七分钟
长方形法
a2-b2
(2a+2b)(a-b)/2
2.几何验证:
你能用下图的面积来解释公式吗?
梯形法
平方差公式:
两个数的和与这两个数的差的积,等于这两个数的平方差。
发现规律:
(a+b)(a-b)
=
a2
-
b2
相同项
相反项
相同项的平方
相反项的平方
平方差公式的特征:
两数和×两数差=(符号相同项)?-
(符号相反项)?
(a+b)(a-b)=a2-b2
公式中的a,b可以表示一个单项式也可以表示一个多项式.
注意事项:
您能从下列式子里找出平方差公式中的
“朋友a”和“朋友b”吗?
(1)(2x-3)(2x+3)
(2)(-2x+3)(-2x-3)
(3)(3-2x)(-2x-3)
(4)(2y-x)(-2y-x)
(5)(-x+2y)(-x-2y)
(6)(-3x+2)(3x+2)
a=2x
b=3
a=-2x
b=3
a=-2x
b=3
a=-x
b=2y
a=-x
b=2y
a=2
b=3x
练习:当堂训练1
二练
十分钟
(不能)
1.下列各式中,能用平方差公式运算
的是(
)
A.(-a+b)(-a-b)
B.(a-b)(b-a)
C.(2a-3b)(3a+2b)
D.(a-b+c)(b-a-c)
2.下列多项式相乘,不能用平方差公式
计算的是(
)
A.(x-2y)(2y+x)
B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y)
D.(-2b-5)(2b-5)
A
C
练习:当堂训练1
二练
二分钟
例
用平方差公式计算:102×98
102
×98
=
(100+2)
(100-2)
=
1002-22
=
10000-4
=
9996
解:
×
二分钟
498
×502
=
(500-2)
(500+2)
=
5002-22
=
250000-4
=
249996
解:
×
练习:当堂训练2
利用平方差公式计算:
498×502
三分钟
例
利用平方差公式计算:
解:
三分钟
计算:
1、(2+1)(22+1)(24+1)(28+1)+1
练习:当堂训练3
运用平方差公式计算:
1、(m+n)(-n+m)
=
2、(-x-y)
(-x+y)
=
3、(2a+b)(2a-b)
=
4、(x2+y2)(x2-y2)=
5、
99
×
101
=
m2-n2
x2-y2
4a2-b2
x4-y4
1002-12=9999
(a+b)(a-b)=a2-b2
课堂小结
通过本节课的学习,你收获了什么?
课后练习
课本P88
课内练习1、2
习题A组1、2
1.什么是平方差公式?
2.运用公式要注意什么?
小结
4.计算:
(1)
(3x+2)(3x-2)=
(2)
(b+2a)(2a-b)=
(3)
(-x+2y)(-x-2y)=
9x2-4
4a2-b2
x2-4y2
练习:当堂训练
练习:当堂训练3
计算
20042
-
2003×2005
解:
20042
-
2003×2005
=
20042
-(2004-1)×(2004+1)
=
20042
-
(20042-12
)
=
20042
-
20042+12
—去括号变号
=1
运用新知
例1、(1)(4m+3)(1-2c)
(2)
(-x+3y)(-x-3y)
哪个是
a
哪个是
b
x?-9y?
解:
(a
+b)
(a-b)
=
1?-(2c)?
=
(1)(1+2c)(1-2c)
=
(2)(-x+3y)(-x-3y)=
(-x)?–(3y)?=
(a
+
b)
(
a
-
b)
=
1-4c?
a?-
b?
a?
-
b?
两数和×两数差=(符号相同项)?-
(符号相反项)?
二分钟
一练
(不能)
(能)
(能)
(不能)
3.下列各式能否用平方差公式
进行计算?
⑶
练习:当堂训练2
P88习题A组2(2)(4)、3、4(2)
作业
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
