北师大版数学七年级下 第5章 生活中的轴对称 单元练习含答案
文档属性
| 名称 | 北师大版数学七年级下 第5章 生活中的轴对称 单元练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 213.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 13:56:19 | ||
图片预览

文档简介
第5章
生活中的轴对称
一.选择题(共10小题)
1.下列交通标志图案是轴对称图形的是( )
A.
B.
C.
D.
2.将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到( )
A.
B.
C.
D.
3.在下列图形中,其中是轴对称图形且有四条对称轴的是( )
A.
B.
C.
D.
4.如图,△ABC中,D点在BC上,∠B=62°,∠C=53°,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF.则∠EAF的度数为( )
A.124°
B.115°
C.130°
D.106°
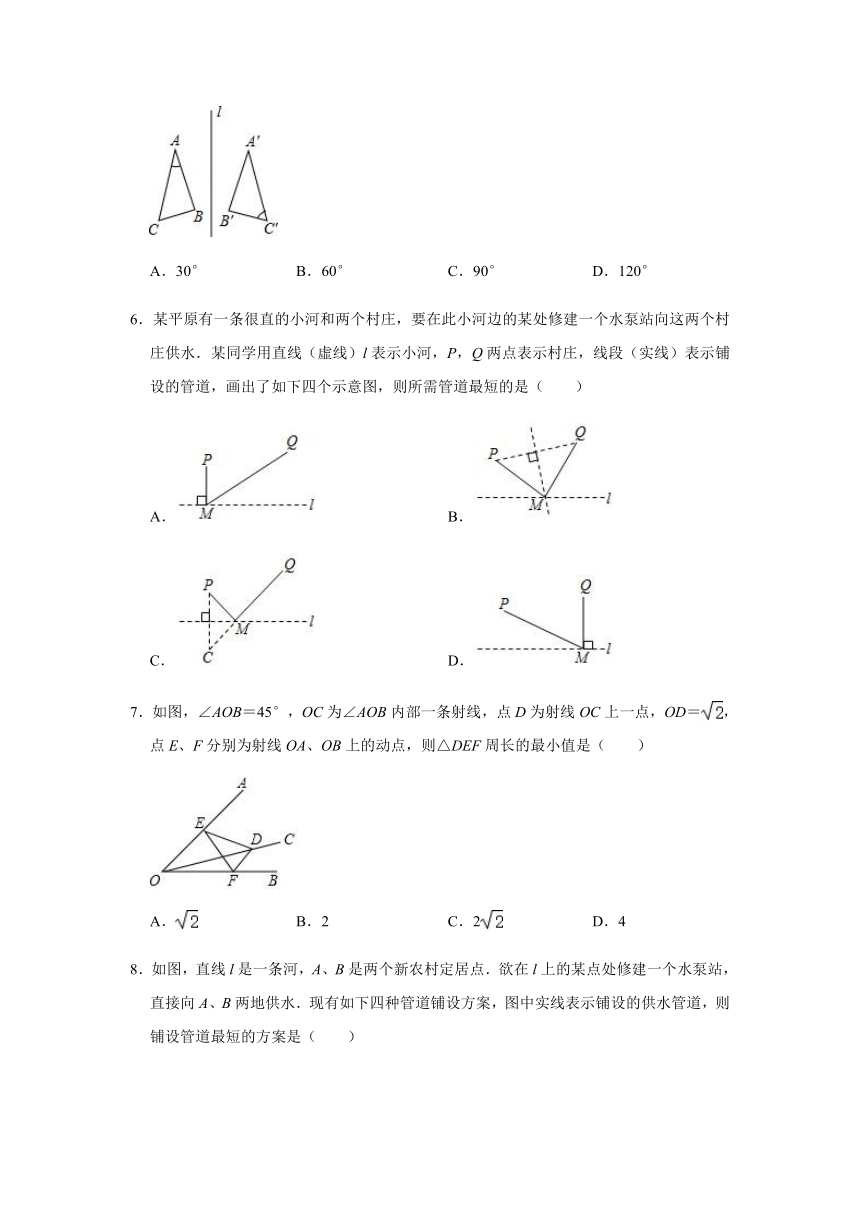
5.如图,∠A=30°,∠C′=60°,△ABC与△A′B′C′关于直线l对称,则∠B度数为( )
A.30°
B.60°
C.90°
D.120°
6.某平原有一条很直的小河和两个村庄,要在此小河边的某处修建一个水泵站向这两个村庄供水.某同学用直线(虛线)l表示小河,P,Q两点表示村庄,线段(实线)表示铺设的管道,画出了如下四个示意图,则所需管道最短的是( )
A.
B.
C.
D.
7.如图,∠AOB=45°,OC为∠AOB内部一条射线,点D为射线OC上一点,OD=,点E、F分别为射线OA、OB上的动点,则△DEF周长的最小值是( )
A.
B.2
C.2
D.4
8.如图,直线l是一条河,A、B是两个新农村定居点.欲在l上的某点处修建一个水泵站,直接向A、B两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管道最短的方案是( )
A.
B.
C.
D.
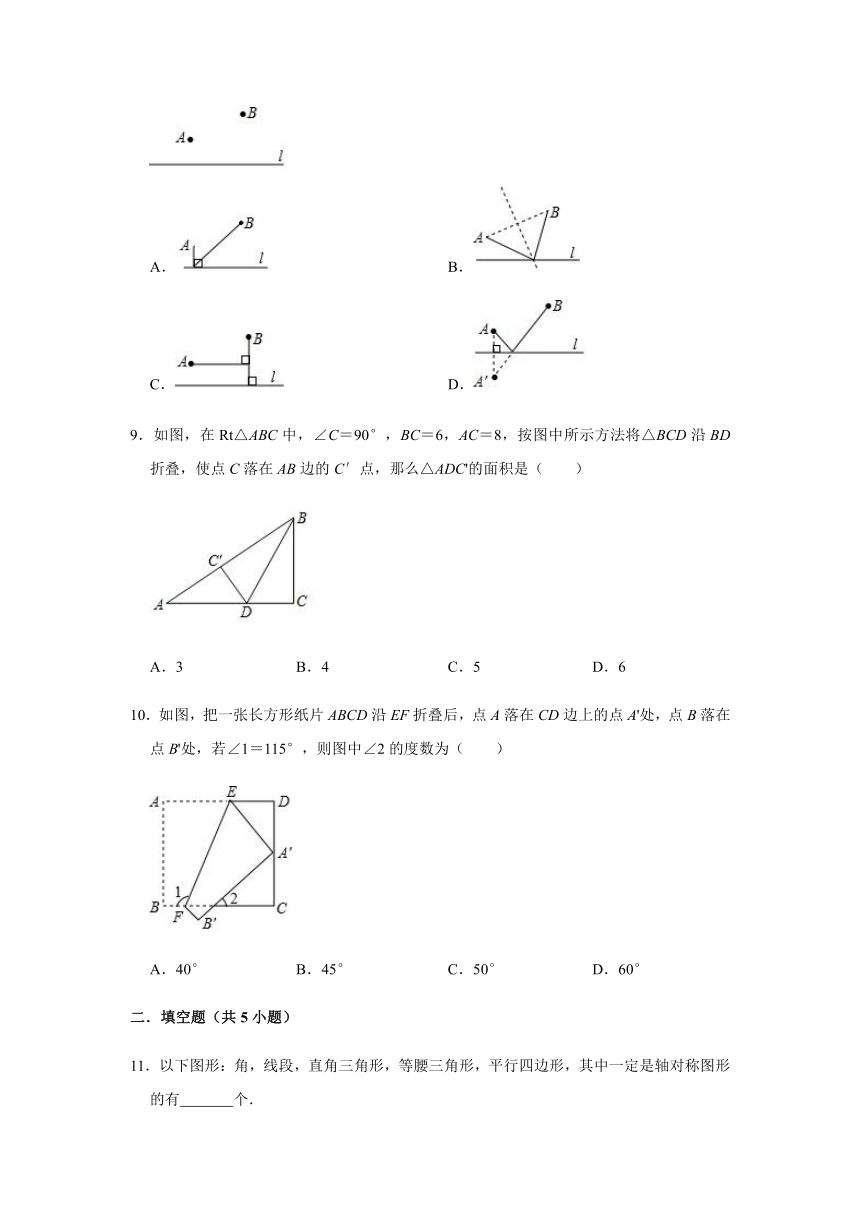
9.如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC'的面积是( )
A.3
B.4
C.5
D.6
10.如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点A'处,点B落在点B'处,若∠1=115°,则图中∠2的度数为( )
A.40°
B.45°
C.50°
D.60°
二.填空题(共5小题)
11.以下图形:角,线段,直角三角形,等腰三角形,平行四边形,其中一定是轴对称图形的有
个.
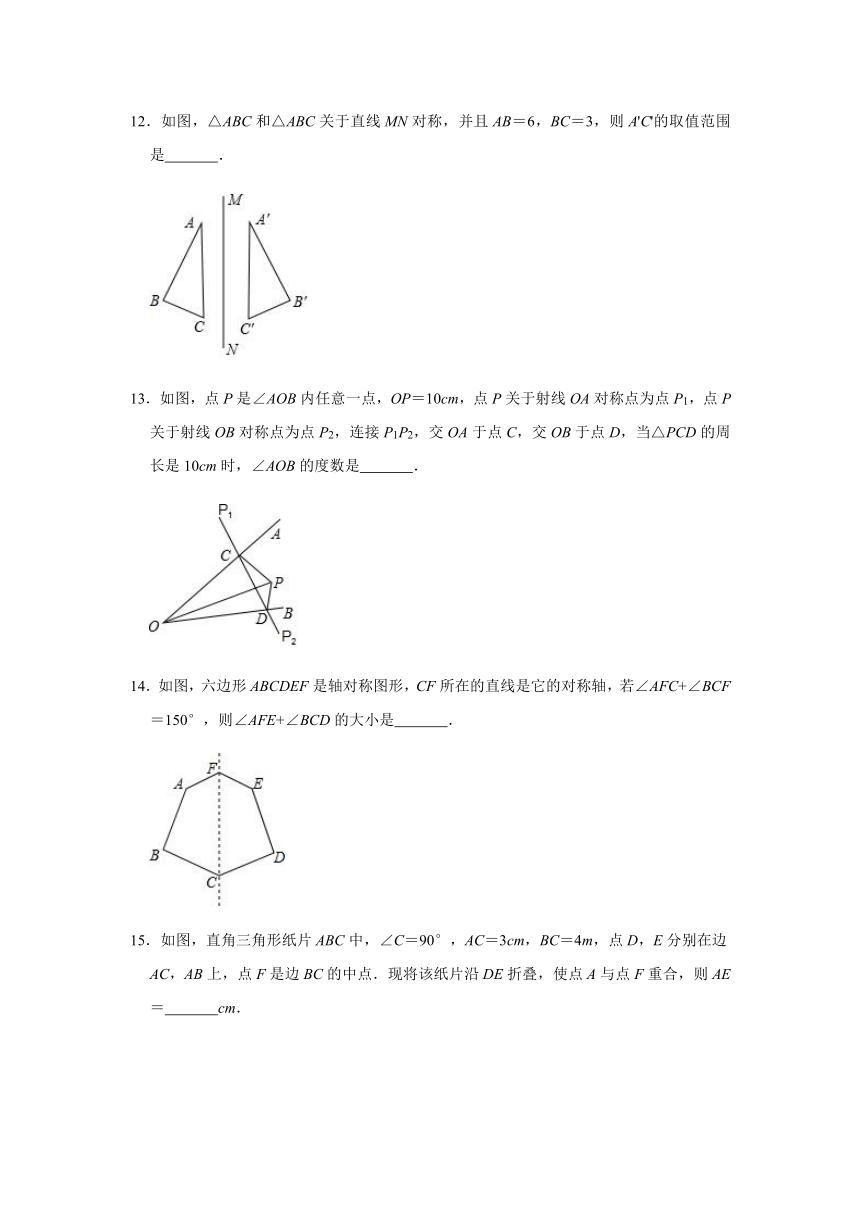
12.如图,△ABC和△ABC关于直线MN对称,并且AB=6,BC=3,则A'C'的取值范围是
.
13.如图,点P是∠AOB内任意一点,OP=10cm,点P关于射线OA对称点为点P1,点P关于射线OB对称点为点P2,连接P1P2,交OA于点C,交OB于点D,当△PCD的周长是10cm时,∠AOB的度数是
.
14.如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD的大小是
.
15.如图,直角三角形纸片ABC中,∠C=90°,AC=3cm,BC=4m,点D,E分别在边AC,AB上,点F是边BC的中点.现将该纸片沿DE折叠,使点A与点F重合,则AE=
cm.
三.解答题(共6小题)
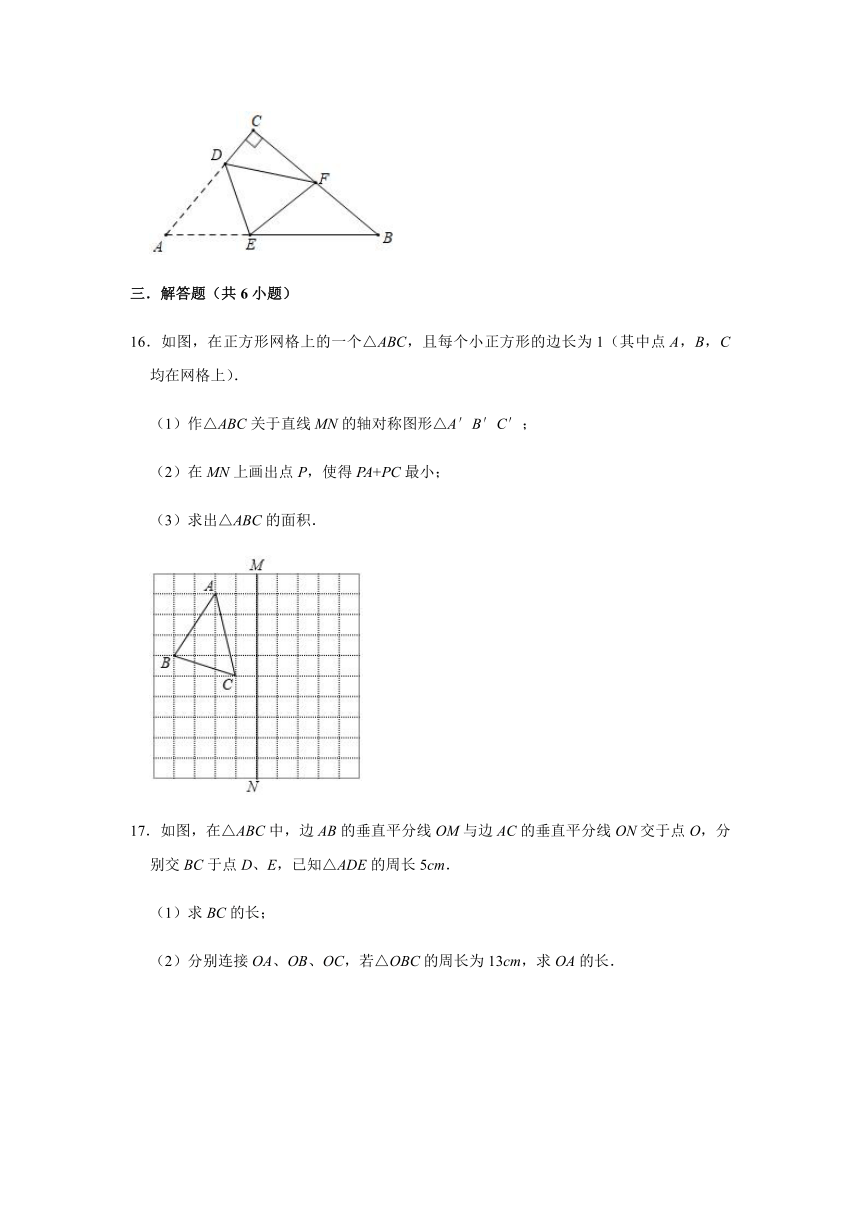
16.如图,在正方形网格上的一个△ABC,且每个小正方形的边长为1(其中点A,B,C均在网格上).
(1)作△ABC关于直线MN的轴对称图形△A′B′C′;
(2)在MN上画出点P,使得PA+PC最小;
(3)求出△ABC的面积.
17.如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,分别交BC于点D、E,已知△ADE的周长5cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为13cm,求OA的长.
18.如图,在△ABC中,∠C=90°,将△ACE沿着AE折叠以后C点正好落在AB边上的点D处.当∠B=28°时,求∠CAE的度数;
19.如图,已知△ABC,点B在直线a上,直线a,b相交于点O.
(1)画△ABC关于直线a对称的△A1B1C1;
(2)在直线b上画出点P,使BP+CP最小.
20.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为多少?
21.按要求作图:
(1)已知线段AB和直线l,画出线段AB关于直线l的对称图形;
(2)如图,牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.
参考答案
一.选择题(共10小题)
1.
B.
2.
C.
3.
C.
4.
C.
5.
C.
6.C.
7.
B.
8.
D.
9.
D.
10.
A.
二.填空题(共5小题)
11.
3.
12.
3<A′C′<9.
13.
30°
14.
300°.
15.
.
三.解答题(共6小题)
16.解:(1)如图,△A′B′C′为所作;
(2)如图,点P为所作;
(3)△ABC的面积=3×4﹣×1×3﹣×3×2﹣×4×1=.
17.解:(1)∵DM是线段AB的垂直平分线,
∴DA=DB,
同理,EA=EC,
∵△ADE的周长5,
∴AD+DE+EA=5,
∴BC=DB+DE+EC=AD+DE+EA=5(cm);
(2)∵△OBC的周长为13,
∴OB+OC+BC=13,
∵BC=5,
∴OB+OC=8,
∵OM垂直平分AB,
∴OA=OB,
同理,OA=OC,
∴OA=OB=OC=4(cm).
18.解:在Rt△ABC中,∠ABC=90°,∠B=28°,
∴∠BAC=90°﹣28°=62°,
∵△ACE沿着AE折叠以后C点正好落在点D处,
∴∠CAE=∠CAB=×62°=31°;
19.解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,点P即为所求.
20.解:过E作EM∥BC,交AD于N,
∵AC=4,AE=2,
∴EC=2=AE,
∴AM=BM=2,
∴AM=AE,
∵AD是BC边上的中线,△ABC是等边三角形,
∴AD⊥BC,
∵EM∥BC,
∴AD⊥EM,
∵AM=AE,
∴E和M关于AD对称,
连接CM交AD于F,连接EF,
则此时EF+CF的值最小,
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC,
∵AM=BM,
∴∠ECF=∠ACB=30°.
21.解:(1)如图所示:
,
线段A′B′即为所求;
(2)如图所示:
,
从A到C,再到D,再到B.
生活中的轴对称
一.选择题(共10小题)
1.下列交通标志图案是轴对称图形的是( )
A.
B.
C.
D.
2.将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到( )
A.
B.
C.
D.
3.在下列图形中,其中是轴对称图形且有四条对称轴的是( )
A.
B.
C.
D.
4.如图,△ABC中,D点在BC上,∠B=62°,∠C=53°,将D点分别以AB、AC为对称轴,画出对称点E、F,并连接AE、AF.则∠EAF的度数为( )
A.124°
B.115°
C.130°
D.106°
5.如图,∠A=30°,∠C′=60°,△ABC与△A′B′C′关于直线l对称,则∠B度数为( )
A.30°
B.60°
C.90°
D.120°
6.某平原有一条很直的小河和两个村庄,要在此小河边的某处修建一个水泵站向这两个村庄供水.某同学用直线(虛线)l表示小河,P,Q两点表示村庄,线段(实线)表示铺设的管道,画出了如下四个示意图,则所需管道最短的是( )
A.
B.
C.
D.
7.如图,∠AOB=45°,OC为∠AOB内部一条射线,点D为射线OC上一点,OD=,点E、F分别为射线OA、OB上的动点,则△DEF周长的最小值是( )
A.
B.2
C.2
D.4
8.如图,直线l是一条河,A、B是两个新农村定居点.欲在l上的某点处修建一个水泵站,直接向A、B两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管道最短的方案是( )
A.
B.
C.
D.
9.如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC'的面积是( )
A.3
B.4
C.5
D.6
10.如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点A'处,点B落在点B'处,若∠1=115°,则图中∠2的度数为( )
A.40°
B.45°
C.50°
D.60°
二.填空题(共5小题)
11.以下图形:角,线段,直角三角形,等腰三角形,平行四边形,其中一定是轴对称图形的有
个.
12.如图,△ABC和△ABC关于直线MN对称,并且AB=6,BC=3,则A'C'的取值范围是
.
13.如图,点P是∠AOB内任意一点,OP=10cm,点P关于射线OA对称点为点P1,点P关于射线OB对称点为点P2,连接P1P2,交OA于点C,交OB于点D,当△PCD的周长是10cm时,∠AOB的度数是
.
14.如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD的大小是
.
15.如图,直角三角形纸片ABC中,∠C=90°,AC=3cm,BC=4m,点D,E分别在边AC,AB上,点F是边BC的中点.现将该纸片沿DE折叠,使点A与点F重合,则AE=
cm.
三.解答题(共6小题)
16.如图,在正方形网格上的一个△ABC,且每个小正方形的边长为1(其中点A,B,C均在网格上).
(1)作△ABC关于直线MN的轴对称图形△A′B′C′;
(2)在MN上画出点P,使得PA+PC最小;
(3)求出△ABC的面积.
17.如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,分别交BC于点D、E,已知△ADE的周长5cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为13cm,求OA的长.
18.如图,在△ABC中,∠C=90°,将△ACE沿着AE折叠以后C点正好落在AB边上的点D处.当∠B=28°时,求∠CAE的度数;
19.如图,已知△ABC,点B在直线a上,直线a,b相交于点O.
(1)画△ABC关于直线a对称的△A1B1C1;
(2)在直线b上画出点P,使BP+CP最小.
20.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为多少?
21.按要求作图:
(1)已知线段AB和直线l,画出线段AB关于直线l的对称图形;
(2)如图,牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.
参考答案
一.选择题(共10小题)
1.
B.
2.
C.
3.
C.
4.
C.
5.
C.
6.C.
7.
B.
8.
D.
9.
D.
10.
A.
二.填空题(共5小题)
11.
3.
12.
3<A′C′<9.
13.
30°
14.
300°.
15.
.
三.解答题(共6小题)
16.解:(1)如图,△A′B′C′为所作;
(2)如图,点P为所作;
(3)△ABC的面积=3×4﹣×1×3﹣×3×2﹣×4×1=.
17.解:(1)∵DM是线段AB的垂直平分线,
∴DA=DB,
同理,EA=EC,
∵△ADE的周长5,
∴AD+DE+EA=5,
∴BC=DB+DE+EC=AD+DE+EA=5(cm);
(2)∵△OBC的周长为13,
∴OB+OC+BC=13,
∵BC=5,
∴OB+OC=8,
∵OM垂直平分AB,
∴OA=OB,
同理,OA=OC,
∴OA=OB=OC=4(cm).
18.解:在Rt△ABC中,∠ABC=90°,∠B=28°,
∴∠BAC=90°﹣28°=62°,
∵△ACE沿着AE折叠以后C点正好落在点D处,
∴∠CAE=∠CAB=×62°=31°;
19.解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,点P即为所求.
20.解:过E作EM∥BC,交AD于N,
∵AC=4,AE=2,
∴EC=2=AE,
∴AM=BM=2,
∴AM=AE,
∵AD是BC边上的中线,△ABC是等边三角形,
∴AD⊥BC,
∵EM∥BC,
∴AD⊥EM,
∵AM=AE,
∴E和M关于AD对称,
连接CM交AD于F,连接EF,
则此时EF+CF的值最小,
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC,
∵AM=BM,
∴∠ECF=∠ACB=30°.
21.解:(1)如图所示:
,
线段A′B′即为所求;
(2)如图所示:
,
从A到C,再到D,再到B.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
