鲁教版(五四制)八年级数学下册第九章图形的相似章节复习课件(共30张PPT)
文档属性
| 名称 | 鲁教版(五四制)八年级数学下册第九章图形的相似章节复习课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 23:10:17 | ||
图片预览



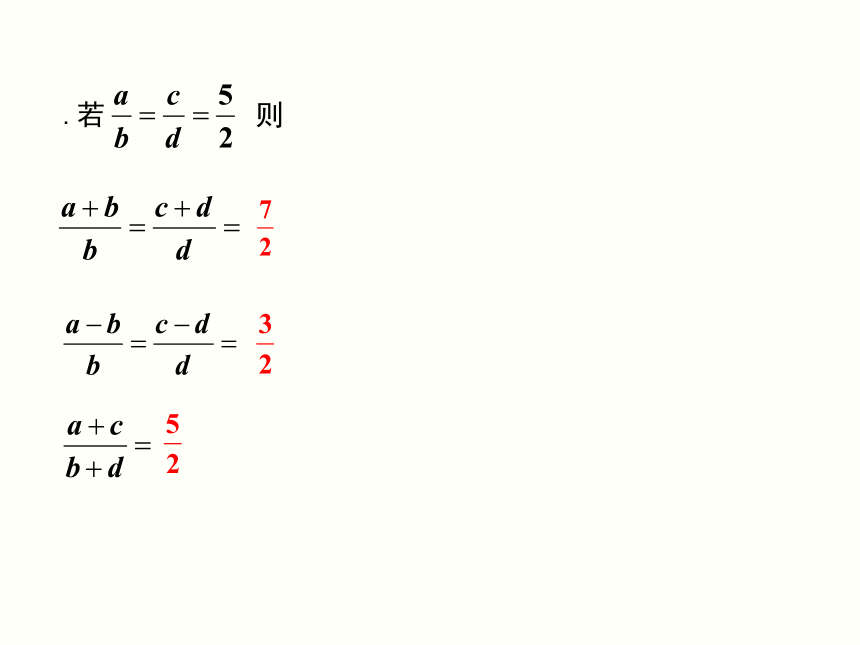





文档简介
(共30张PPT)
小结与复习
第九章
图形的相似
如果选用一个长度单位量得两条线段a
,b
的长度分别为m
,n
.那么两条线段的比
.
四条线段a
,
b
,
c
,
d中,如果a与b的比等于c与d的比,那么这四条线段a
,
b
,
c
,
d叫做成比例线段,简称比例线段.
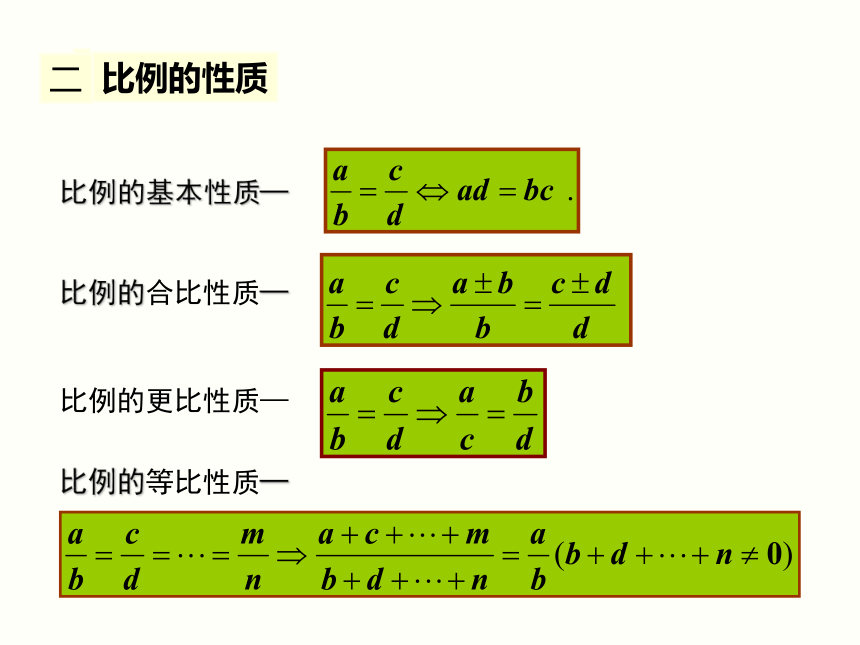
比例的基本性质─
比例的合比性质─
比例的等比性质─
比例的更比性质—
.若
则
那么称线段AB被点C
点C叫做线段AB的
AC与AB(或BC与AC)的比叫做
黄金比
≈0.618
黄金分割
黄金分割点
黄金比
若线段MN=10,点K为MN的黄金分割点,则KM的长为
.
(1)在判断是否成比例线段时,长度单位必须相同,若
长度单位不同,应先统一单位再判断;
(2)在判断是否成比例线段时,应首先将四条线段按长
短顺序排列起来,若两条较短线段的长度的比等于
两条较长的线段的比,则是成比例线段,否则不是.
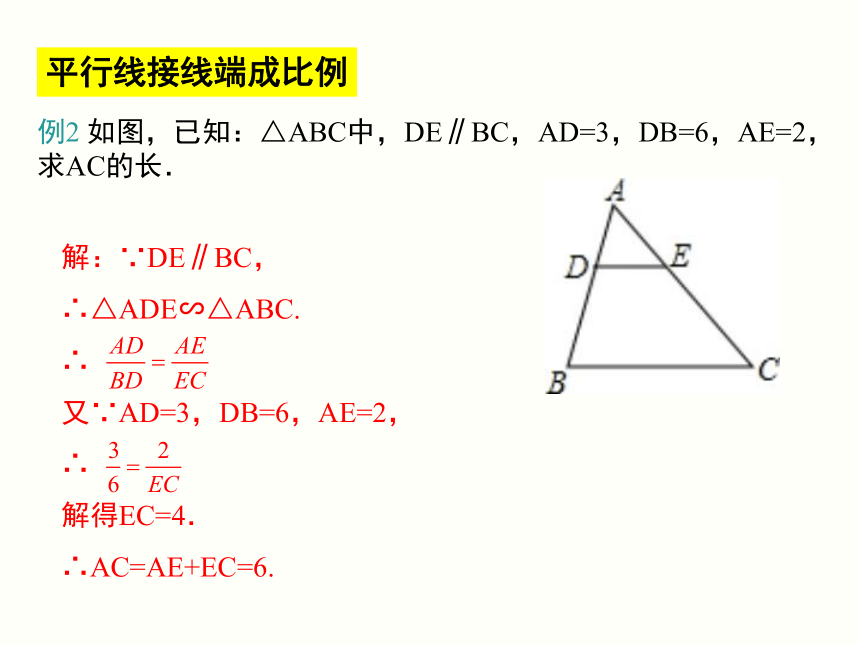
例2
如图,已知:△ABC中,DE∥BC,AD=3,DB=6,AE=2,求AC的长.
解:∵DE∥BC,
∴△ADE∽△ABC.
∴
又∵AD=3,DB=6,AE=2,
∴
解得EC=4.
∴AC=AE+EC=6.
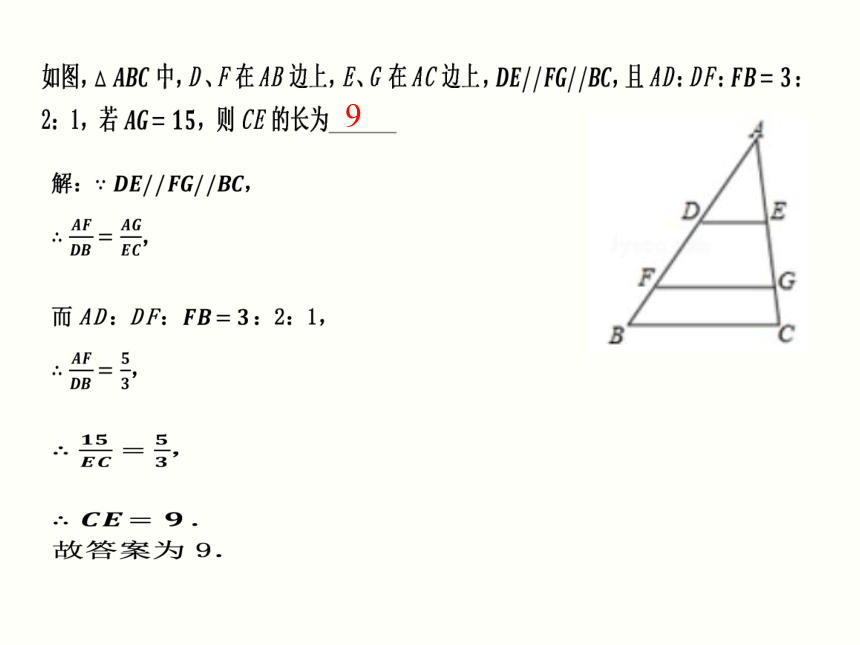
平行线接线端成比例
如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,
,
DE=6,则EF=
___
.
9
12
9
1.定义:
三角对应角相等、三边对应成比例的两个三角形叫相似三角形.
2.判定定理:
(1)两角相等的两个三角形相似
(2)三边对应成比例的两个三角形相似
(3)两边对应成比例且夹角相等的两个三角形相似
3.性质:
(1)相似三角形对应角相等,对应边成比例
(2)相似三角形对应高的比,对应角平分线的比和对应中线的
比都等于相似比
★相似三角形周长的比等于
相似比
★相似三角形面积的比等于
相似比的平方
★相似多边形的周长比等于
相似比
★相似多边形面积的比等于
相似比的平方
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
求证:△ABD∽△CED;
解:(1)∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,∠ACF=120°.
∵CE是外角平分线,∴∠ACE=60°.
∴∠BAC=∠ACE.
又∵∠ADB=∠CDE,∴△ABD∽△CED.
.如图,在△ABC中,已知DE//BC,AD=3BD,S△ABC=48,求S△ADE.
A
B
C
D
E
3
1
解:∵
DE∥BC,
∴△ADE∽△ABC.
∴S△ABC
:
S△ADE
=
∵AD
:
BD
=
1:3,
∴AD
:
AB
=
1:4.
∴S△ADE=27.
(1)
测高
测量不能到达两点间的距离,常构造相似三角形求解.
(不能直接使用皮尺或刻度尺量的)
(不能直接测量的两点间的距离)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
(2)
测距
例如用相似测物体的高度
测山高
测楼高
测内孔直径
求最大值与最小值
C
100
9
如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形.
★这个点叫做位似中心.
★这两个相似图形的相似比又称为位似比.
★位似图形上任意一对对应点到位似中心的距离之比等于位似比.
课堂小结
图形的相似
比例线段
相似三角形
相似多边形
位似
比例的基本性质
比例线段
平行线分线段成比例
判定
性质
应用
当堂检测
1、D是△ABC的边AB上的点,
请你添加一个条件,使△ACD与△ABC相似,
这个条件是(
)
①∠ADC=∠ACB
②
∠ACD=∠B
③
2、如果一个三角形三边长分别为5、12、13,与其相似的三角形最大边是39,则该三角形最短的边长为(
)
15
①②③
当堂检测
3、
当堂检测
4、如图,铁道口的栏杆的短臂长1.25米,长臂长16.5米,当短臂端点下降0.85米时,长臂端点升高(
)(杆的宽度忽略不计)
11.22米
当堂检测
5、如图,身高为1.6m的某同学想测量一棵大树的高度,她沿树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树高为(
)
A、4.8m
B、6.4m
C、8m
D、10m
解:依题意知:EC⊥AB,于点C,DB⊥AB于点B,
∴CE∥DB
∴△ACE∽△ABD
∴AC:AB=CE:BD
∵AC=0.8m,BC=3.2m
∴AB=AC+CB=4m
CE=1.6m
∴0.8:4=1.6:BD
解得:BD=8(m)
∴树高BD为8m。
C
小结与复习
第九章
图形的相似
如果选用一个长度单位量得两条线段a
,b
的长度分别为m
,n
.那么两条线段的比
.
四条线段a
,
b
,
c
,
d中,如果a与b的比等于c与d的比,那么这四条线段a
,
b
,
c
,
d叫做成比例线段,简称比例线段.
比例的基本性质─
比例的合比性质─
比例的等比性质─
比例的更比性质—
.若
则
那么称线段AB被点C
点C叫做线段AB的
AC与AB(或BC与AC)的比叫做
黄金比
≈0.618
黄金分割
黄金分割点
黄金比
若线段MN=10,点K为MN的黄金分割点,则KM的长为
.
(1)在判断是否成比例线段时,长度单位必须相同,若
长度单位不同,应先统一单位再判断;
(2)在判断是否成比例线段时,应首先将四条线段按长
短顺序排列起来,若两条较短线段的长度的比等于
两条较长的线段的比,则是成比例线段,否则不是.
例2
如图,已知:△ABC中,DE∥BC,AD=3,DB=6,AE=2,求AC的长.
解:∵DE∥BC,
∴△ADE∽△ABC.
∴
又∵AD=3,DB=6,AE=2,
∴
解得EC=4.
∴AC=AE+EC=6.
平行线接线端成比例
如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,
,
DE=6,则EF=
___
.
9
12
9
1.定义:
三角对应角相等、三边对应成比例的两个三角形叫相似三角形.
2.判定定理:
(1)两角相等的两个三角形相似
(2)三边对应成比例的两个三角形相似
(3)两边对应成比例且夹角相等的两个三角形相似
3.性质:
(1)相似三角形对应角相等,对应边成比例
(2)相似三角形对应高的比,对应角平分线的比和对应中线的
比都等于相似比
★相似三角形周长的比等于
相似比
★相似三角形面积的比等于
相似比的平方
★相似多边形的周长比等于
相似比
★相似多边形面积的比等于
相似比的平方
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
求证:△ABD∽△CED;
解:(1)∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,∠ACF=120°.
∵CE是外角平分线,∴∠ACE=60°.
∴∠BAC=∠ACE.
又∵∠ADB=∠CDE,∴△ABD∽△CED.
.如图,在△ABC中,已知DE//BC,AD=3BD,S△ABC=48,求S△ADE.
A
B
C
D
E
3
1
解:∵
DE∥BC,
∴△ADE∽△ABC.
∴S△ABC
:
S△ADE
=
∵AD
:
BD
=
1:3,
∴AD
:
AB
=
1:4.
∴S△ADE=27.
(1)
测高
测量不能到达两点间的距离,常构造相似三角形求解.
(不能直接使用皮尺或刻度尺量的)
(不能直接测量的两点间的距离)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
(2)
测距
例如用相似测物体的高度
测山高
测楼高
测内孔直径
求最大值与最小值
C
100
9
如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形.
★这个点叫做位似中心.
★这两个相似图形的相似比又称为位似比.
★位似图形上任意一对对应点到位似中心的距离之比等于位似比.
课堂小结
图形的相似
比例线段
相似三角形
相似多边形
位似
比例的基本性质
比例线段
平行线分线段成比例
判定
性质
应用
当堂检测
1、D是△ABC的边AB上的点,
请你添加一个条件,使△ACD与△ABC相似,
这个条件是(
)
①∠ADC=∠ACB
②
∠ACD=∠B
③
2、如果一个三角形三边长分别为5、12、13,与其相似的三角形最大边是39,则该三角形最短的边长为(
)
15
①②③
当堂检测
3、
当堂检测
4、如图,铁道口的栏杆的短臂长1.25米,长臂长16.5米,当短臂端点下降0.85米时,长臂端点升高(
)(杆的宽度忽略不计)
11.22米
当堂检测
5、如图,身高为1.6m的某同学想测量一棵大树的高度,她沿树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树高为(
)
A、4.8m
B、6.4m
C、8m
D、10m
解:依题意知:EC⊥AB,于点C,DB⊥AB于点B,
∴CE∥DB
∴△ACE∽△ABD
∴AC:AB=CE:BD
∵AC=0.8m,BC=3.2m
∴AB=AC+CB=4m
CE=1.6m
∴0.8:4=1.6:BD
解得:BD=8(m)
∴树高BD为8m。
C
