鲁教版(五四制)八年级数学下册第六章特殊的平行四边形章节复习课件(共34张PPT)
文档属性
| 名称 | 鲁教版(五四制)八年级数学下册第六章特殊的平行四边形章节复习课件(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 23:15:09 | ||
图片预览







文档简介
(共34张PPT)
矩形、菱形、正方形
第6章
特殊的平行四边形
基础复习?????菱形
温馨提示????(1)菱形既是轴对称图形,又是中心对称图形.它有2条对称轴,分别是对角线所在的直线;对称中心是两条对角线的交
点.(2)菱形的对角线把菱形分为四个全等的直角三角形.
定义
有一组⑨????邻边相等????的平行四边形是菱形
性质
(1)菱形具有⑩????平行四边形????的一切性质;
(2)菱形的四条边都?????相等????;
(3)菱形的两条对角线?????互相垂直????,并且每一条对角线?????平分一
组对角????;
(4)菱形的面积等于两条对角线长?????乘积的一半????
判定
(1)定义法:有?????一组邻边????相等的平行四边形是菱形;
(2)对角线互相?????垂直????的平行四边形是菱形;
(3)?????四条边????都相等的四边形是菱形
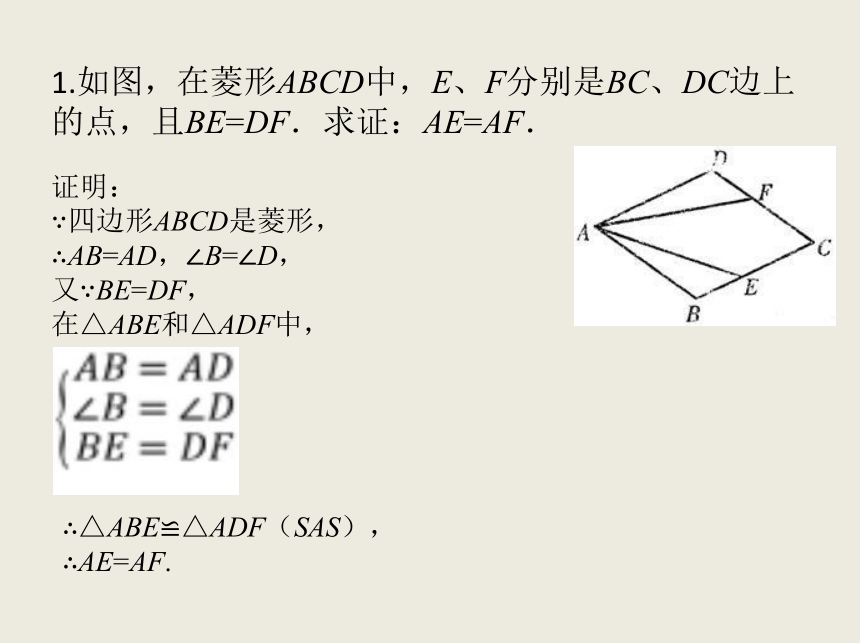
1.如图,在菱形ABCD中,E、F分别是BC、DC边上的点,且BE=DF.求证:AE=AF.
证明:
∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
又∵BE=DF,
在△ABE和△ADF中,
∴△ABE≌△ADF(SAS),
∴AE=AF.
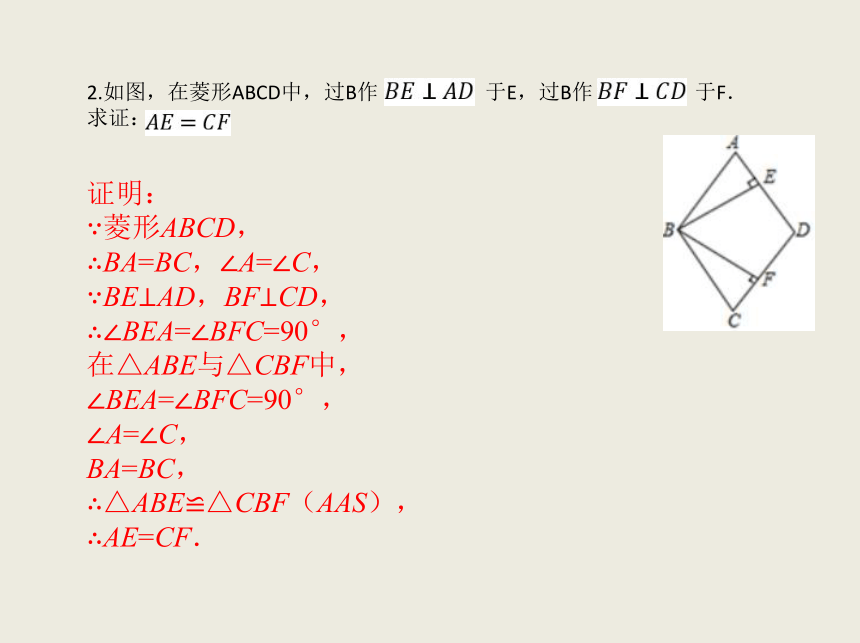
2.如图,在菱形ABCD中,过B作
于E,过B作
于F.
求证:
证明:
∵菱形ABCD,
∴BA=BC,∠A=∠C,
∵BE⊥AD,BF⊥CD,∴∠BEA=∠BFC=90°,
在△ABE与△CBF中,∠BEA=∠BFC=90°,
∠A=∠C,
BA=BC,
∴△ABE≌△CBF(AAS),∴AE=CF.
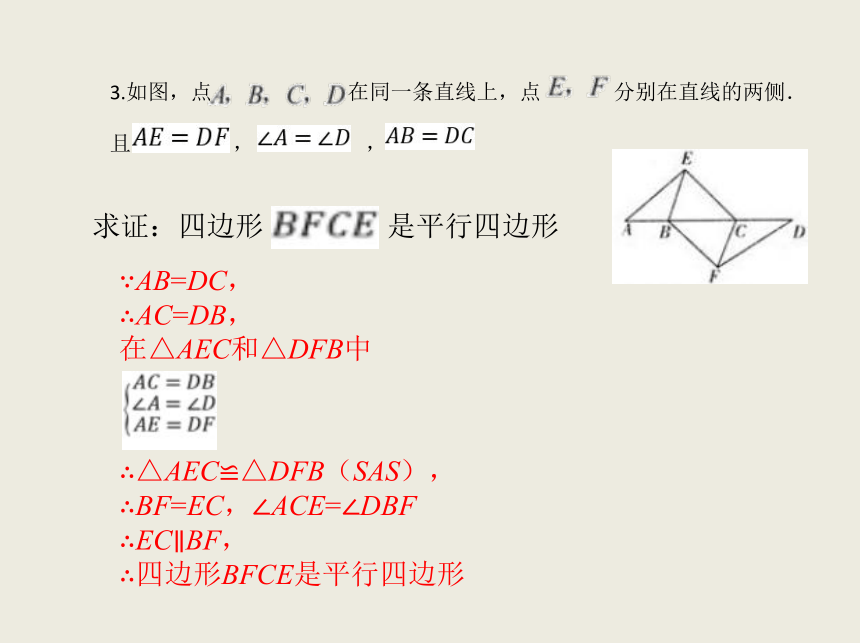
3.如图,点
在同一条直线上,点
分别在直线的两侧.
且
,
,
求证:四边形
是平行四边形
∵AB=DC,
∴AC=DB,
在△AEC和△DFB中
∴△AEC≌△DFB(SAS),
∴BF=EC,∠ACE=∠DBF
∴EC∥BF,
∴四边形BFCE是平行四边形
3.如图,点
在同一条直线上,点
分别在直线的两侧.
且
,
,
若
,
,
,
则当
_______时,四边形
是菱形.
4
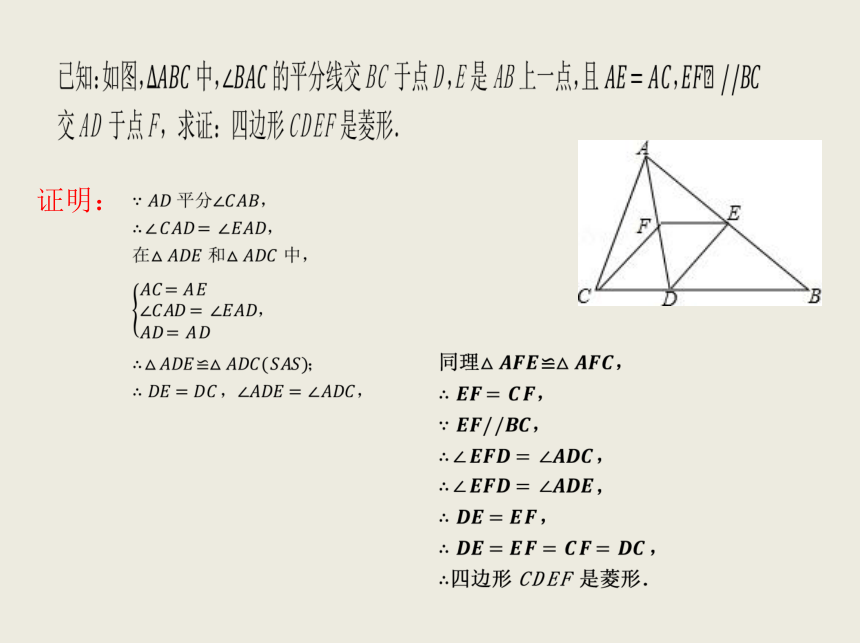
证明:
基础复习????矩形
定义
有①????一个角是直角????的平行四边形叫做矩形
性质
(1)矩形具有②????平行四边形????的一切性质;
(2)矩形的四个角都是③????直角????;
(3)矩形的对角线④????相等????
判定
(1)定义法:有一个角是直角的⑤????平行四边形????是矩形;
(2)对角线⑥????相等????的平行四边形是矩形;
(3)有⑦????三个角????都是直角的四边形是矩形;
(4)对角线⑧????相等且互相平分????的四边形是矩形
证明:
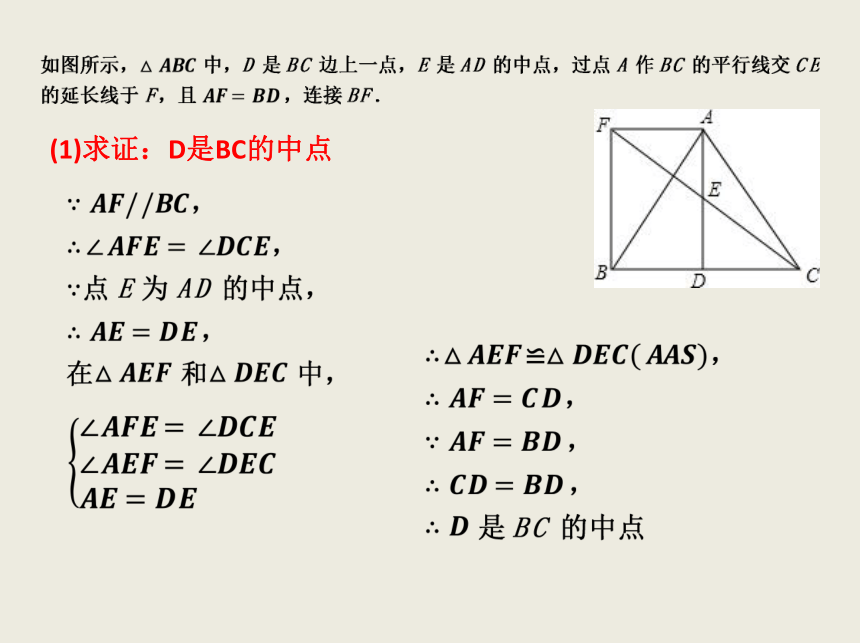
(1)求证:D是BC的中点
变式1-1????如图,在矩形ABCD中,AD=AE,DF⊥AE于点
F.求证:AB=DF.
证明 ∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠AEB=∠DAF,
∵DF⊥AE,∴∠AFD=90°,
在△ABE和△DFA中,
∵?
∴△ABE≌△DFA,
∴AB=DF.
方法技巧
矩形是特殊的平行四边形,其特殊性在于内角均为
直角,故在应用其性质时常会和直角三角形相结合.
基础复习?????正方形
温馨提示????(1)正方形既是轴对称图形,又是中心对称图形,它有4
条对称轴.(2)正方形的对角线把正方形分成四个全等的等腰直角
三角形.
定义
有一组?????邻边相等????的矩形叫做正方形
性质
(1)正方形的四条边都?????相等????,两组对边分别?????平行????;
(2)正方形的四个角都等于?????90°????;
(3)正方形的对角线互相?????垂直、平分且相等????,每条对角线平分一
组对角
判定
(1)定义法;
(2)对角线?????相等????的菱形是正方形;
(3)对角线?????垂直????的矩形是正方形;
(4)有一个角是直角的?????菱形????是正方形
1.
如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且
,延长EF交BC的延长线于点G.
1.
如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且
,延长EF交BC的延长线于点G.
基础复习?????平行四边形、矩形、菱形、正方形的关系
1.平行四边形与特殊平行四边形的包含关系
?
2.从四边形到特殊平行四边形的演变关系
?
温馨提示????依次连接四边形各边的中点所得到的新的四边形的
形状与原四边形的对角线有关系,若对角线相等,则新的四边形是
菱形;若对角线垂直,则新的四边形是矩形.
一、选择题
1.在△ABC中,点D是边BC上的点(与B,C两点不重合),
过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正
确的是?(
D
)?
A.若AD⊥BC,则四边形AEDF是矩形
当堂巩固
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
二、填空题
2.矩形的两条对角线的一个夹角为60°,两条对角
线的长度的和为8
cm,则这个矩形的一条较长边的长为?????2?????
cm.
解析 如图,∵四边形ABCD是矩形,
∴∠ABC=90°,AC=BD=4
cm,OA=OC,OD=OB,
∴OA=OB=2
cm,由题意得∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=?AC=2
cm.
在Rt△ABC中,
由勾股定理得BC=
?
=2?
cm.
这个矩形的一条较长边的长为2?
cm.
3.边长为5
cm的菱形的一条对角线的长是6
cm,
则另一条对角线的长是????8????cm.
解析 如图,在菱形ABCD中,AB=5
cm,AC=6
cm,
∵对角线互相垂直平分,
∴∠AOB=90°,AO=3
cm.
在Rt△AOB中,BO=?
=4
cm,
∴BD=2BO=8
cm.
4.如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在
BC、CD上,若AE=?,∠EAF=45°,则AF的长为?????????.
?
5.如图,在矩形ABCD中,BE⊥AC,BE交AC,AD于点F,E,
若AD=1,AB=CF,则AE=?????????.
?
6.如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中
点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理
由.
解析 (1)证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=DC=AD,
∵点E,O,F分别为AB,AC,AD的中点,
∴AE=BE=DF=AF,OF=?DC,OE=?BC,OE∥BC.
在△BCE和△DCF中,?
∴△BCE≌△DCF(SAS).
(2)当AB⊥BC时,四边形AEOF是正方形.理由如下:
由(1)得AE=OE=OF=AF,
∴四边形AEOF是菱形.
∵AB⊥BC,OE∥BC,
∴OE⊥AB,∴∠AEO=90°,
∴四边形AEOF是正方形.
谢谢观看!
矩形、菱形、正方形
第6章
特殊的平行四边形
基础复习?????菱形
温馨提示????(1)菱形既是轴对称图形,又是中心对称图形.它有2条对称轴,分别是对角线所在的直线;对称中心是两条对角线的交
点.(2)菱形的对角线把菱形分为四个全等的直角三角形.
定义
有一组⑨????邻边相等????的平行四边形是菱形
性质
(1)菱形具有⑩????平行四边形????的一切性质;
(2)菱形的四条边都?????相等????;
(3)菱形的两条对角线?????互相垂直????,并且每一条对角线?????平分一
组对角????;
(4)菱形的面积等于两条对角线长?????乘积的一半????
判定
(1)定义法:有?????一组邻边????相等的平行四边形是菱形;
(2)对角线互相?????垂直????的平行四边形是菱形;
(3)?????四条边????都相等的四边形是菱形
1.如图,在菱形ABCD中,E、F分别是BC、DC边上的点,且BE=DF.求证:AE=AF.
证明:
∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
又∵BE=DF,
在△ABE和△ADF中,
∴△ABE≌△ADF(SAS),
∴AE=AF.
2.如图,在菱形ABCD中,过B作
于E,过B作
于F.
求证:
证明:
∵菱形ABCD,
∴BA=BC,∠A=∠C,
∵BE⊥AD,BF⊥CD,∴∠BEA=∠BFC=90°,
在△ABE与△CBF中,∠BEA=∠BFC=90°,
∠A=∠C,
BA=BC,
∴△ABE≌△CBF(AAS),∴AE=CF.
3.如图,点
在同一条直线上,点
分别在直线的两侧.
且
,
,
求证:四边形
是平行四边形
∵AB=DC,
∴AC=DB,
在△AEC和△DFB中
∴△AEC≌△DFB(SAS),
∴BF=EC,∠ACE=∠DBF
∴EC∥BF,
∴四边形BFCE是平行四边形
3.如图,点
在同一条直线上,点
分别在直线的两侧.
且
,
,
若
,
,
,
则当
_______时,四边形
是菱形.
4
证明:
基础复习????矩形
定义
有①????一个角是直角????的平行四边形叫做矩形
性质
(1)矩形具有②????平行四边形????的一切性质;
(2)矩形的四个角都是③????直角????;
(3)矩形的对角线④????相等????
判定
(1)定义法:有一个角是直角的⑤????平行四边形????是矩形;
(2)对角线⑥????相等????的平行四边形是矩形;
(3)有⑦????三个角????都是直角的四边形是矩形;
(4)对角线⑧????相等且互相平分????的四边形是矩形
证明:
(1)求证:D是BC的中点
变式1-1????如图,在矩形ABCD中,AD=AE,DF⊥AE于点
F.求证:AB=DF.
证明 ∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠AEB=∠DAF,
∵DF⊥AE,∴∠AFD=90°,
在△ABE和△DFA中,
∵?
∴△ABE≌△DFA,
∴AB=DF.
方法技巧
矩形是特殊的平行四边形,其特殊性在于内角均为
直角,故在应用其性质时常会和直角三角形相结合.
基础复习?????正方形
温馨提示????(1)正方形既是轴对称图形,又是中心对称图形,它有4
条对称轴.(2)正方形的对角线把正方形分成四个全等的等腰直角
三角形.
定义
有一组?????邻边相等????的矩形叫做正方形
性质
(1)正方形的四条边都?????相等????,两组对边分别?????平行????;
(2)正方形的四个角都等于?????90°????;
(3)正方形的对角线互相?????垂直、平分且相等????,每条对角线平分一
组对角
判定
(1)定义法;
(2)对角线?????相等????的菱形是正方形;
(3)对角线?????垂直????的矩形是正方形;
(4)有一个角是直角的?????菱形????是正方形
1.
如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且
,延长EF交BC的延长线于点G.
1.
如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且
,延长EF交BC的延长线于点G.
基础复习?????平行四边形、矩形、菱形、正方形的关系
1.平行四边形与特殊平行四边形的包含关系
?
2.从四边形到特殊平行四边形的演变关系
?
温馨提示????依次连接四边形各边的中点所得到的新的四边形的
形状与原四边形的对角线有关系,若对角线相等,则新的四边形是
菱形;若对角线垂直,则新的四边形是矩形.
一、选择题
1.在△ABC中,点D是边BC上的点(与B,C两点不重合),
过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正
确的是?(
D
)?
A.若AD⊥BC,则四边形AEDF是矩形
当堂巩固
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形
二、填空题
2.矩形的两条对角线的一个夹角为60°,两条对角
线的长度的和为8
cm,则这个矩形的一条较长边的长为?????2?????
cm.
解析 如图,∵四边形ABCD是矩形,
∴∠ABC=90°,AC=BD=4
cm,OA=OC,OD=OB,
∴OA=OB=2
cm,由题意得∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=?AC=2
cm.
在Rt△ABC中,
由勾股定理得BC=
?
=2?
cm.
这个矩形的一条较长边的长为2?
cm.
3.边长为5
cm的菱形的一条对角线的长是6
cm,
则另一条对角线的长是????8????cm.
解析 如图,在菱形ABCD中,AB=5
cm,AC=6
cm,
∵对角线互相垂直平分,
∴∠AOB=90°,AO=3
cm.
在Rt△AOB中,BO=?
=4
cm,
∴BD=2BO=8
cm.
4.如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在
BC、CD上,若AE=?,∠EAF=45°,则AF的长为?????????.
?
5.如图,在矩形ABCD中,BE⊥AC,BE交AC,AD于点F,E,
若AD=1,AB=CF,则AE=?????????.
?
6.如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中
点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理
由.
解析 (1)证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=DC=AD,
∵点E,O,F分别为AB,AC,AD的中点,
∴AE=BE=DF=AF,OF=?DC,OE=?BC,OE∥BC.
在△BCE和△DCF中,?
∴△BCE≌△DCF(SAS).
(2)当AB⊥BC时,四边形AEOF是正方形.理由如下:
由(1)得AE=OE=OF=AF,
∴四边形AEOF是菱形.
∵AB⊥BC,OE∥BC,
∴OE⊥AB,∴∠AEO=90°,
∴四边形AEOF是正方形.
谢谢观看!
